Return to the list of my pages written in English about the two envelopes problem
One method uses the law of total expectation.
The other method uses calculating formulas of conditional expectations.
For reference.
Let x and y be the amounts in the envelope selected by you and the amount in the another envelope respectively.
Let X and Y be a random variables which take x and y as their value respectively.
For reference.
For reference.
Using this symbol I tried to prove the equivalence of the two envelopes.
Notations
Let x be the amount of money in the envelope selected by you.
Let X be a random variable which take x as its value.
Let a be the lesser amounts in the two envelopes.
Let r ( > 1) is the ratio of the greater amount to the lesser amount.
Let g(a) be the probability or probability density of the event of the pair of amount of money is (a, ra).
Let1/k be the factor of integration by substitution by the change of variables from y (=rx) to x.
If the distribution of amount of money is discreet,1/k = 1 .
If the distribution of amount of money is continuous,dy/dx = r . Therefore 1/k = r .
Let P(x) be the probability or probability density of the event thatX = x .
using P the equivalence of the mean values of X and Y can be proven. ( ← Added on April 1, 2016)
Remarkable thing
The steps from the partition through change of variables correspond to deformation of series.
This fact reminded me of the following articles.
If I illustrate the steps from the partition through change of variables, it will be as follows.
Before
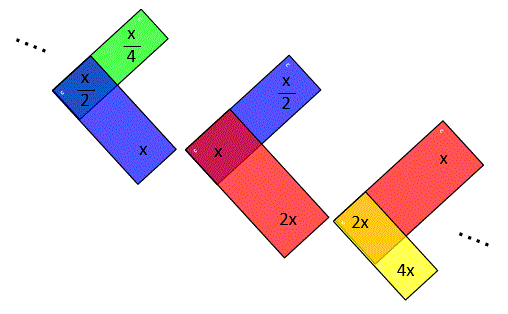
After
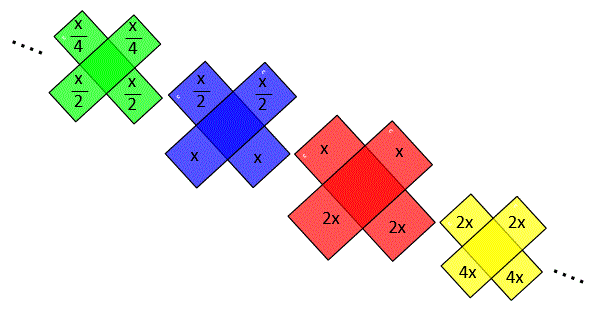
↑ These drawings were added on February 28, 2016.
Addition
Notations
Let x be the amount of money in the envelope selected by you.
Let X be a random variable which take x as its value.
Let Y be a random variable which denotes the amount of money in your new envelope after switching under the condition you always switch.
Let a be the lesser amounts in the two envelopes.
Let r ( > 1) is the ratio of the greater amount to the lesser amount.
Let g(a) be the probability or probability density of the event of the pair of amount of money is (a, ra).
Let1/k be the factor of integration by substitution by the change of variables from y (=rx) to x.
If the distribution of amount of money is discreet,1/k = 1 .
If the distribution of amount of money is continuous,dy/dx = r . Therefore 1/k = r .
Let P(x) be the probability or probability density of the event thatX = x .
Let O(x) be the probability or probability density of the event thatY = x .
Let G(x) be the probability or probability density of the event thatX = x/2 and Y = x .
Let L(x) be the probability or probability density of the event thatX = 2x and Y = x .
using P the equivalence of the distribution of X and Y can be proven.
∴ O(x) = L(x) + G(x) = (1/2)(g(x) + k(g(x/r)) = P(x) .
In other words, the distribution of the amount of money before switch is same as it after switch.
So if mean values are finite they are same.
Return to the list of my pages written in English about the two envelopes problem
2016/04/01 18:55:42
First edition 2016/02/20
 Two methods for the proof of the equivalence of the envelopes of the two envelopes problem
Two methods for the proof of the equivalence of the envelopes of the two envelopes problem
Caution
I who am a Japanese wrote this page in English, but I am not so good at English.
I who am a Japanese wrote this page in English, but I am not so good at English.
Introduction
There are two method to prove the equivalence of the envelopes of the two envelopes problem.One method uses the law of total expectation.
The other method uses calculating formulas of conditional expectations.
A method using the law of total expectation.
The law of total expectation is the theorem that the mean value of the conditional expectation is equal to the unconditional expectation.For reference.
- Article "Law of total expectation" in the English language Wikipedia.
Let x and y be the amounts in the envelope selected by you and the amount in the another envelope respectively.
Let X and Y be a random variables which take x and y as their value respectively.
| step |
amount of money chosen envelope |
amount of money oposit envelope |
|---|---|---|
|
conditional expectations under the condition a=x |
x | E(Y | X=x) |
|
mean values of conditional expectations |
E(X) | E[ E(Y | X=x) ] |
| law of total expectation | E(Y) | |
|
because E(X) = E(Y) |
same as the chosen envelope |
For reference.
A method using calculating formulas of conditional expectations.
Using the calculation formula of conditional expectation, we can prove the equivalence of the two envelopes.For reference.
- Chalmers, D.J. 1994.
- A web page titled "Dan’s Geometrical Curiosities - Maximizing your earnings with money envelopes: a mathematical riddle"
- A web page titled "NaClhv: The two envelopes problem and its solution"
summantegra
Summantegra is made of summation and integral and denoted by a symbol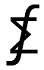 .
.
Summantegra is made of summation and integral and denoted by a symbol
Using this symbol I tried to prove the equivalence of the two envelopes.
Notations
Let x be the amount of money in the envelope selected by you.
Let X be a random variable which take x as its value.
Let a be the lesser amounts in the two envelopes.
Let r ( > 1) is the ratio of the greater amount to the lesser amount.
Let g(a) be the probability or probability density of the event of the pair of amount of money is (a, ra).
Let
If the distribution of amount of money is discreet,
If the distribution of amount of money is continuous,
Let P(x) be the probability or probability density of the event that
using P the equivalence of the mean values of X and Y can be proven. ( ← Added on April 1, 2016)
| step |
amount of money chosen envelope |
amount of money oposit envelope |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
conditional expectations under the condition X=x |
x |
k g(x/r) (x/r) + g(x) rx g(x) + k g(x/r) |
||||||||||||
|
mean values of conditional expectations |
|
|
||||||||||||
|
because P(x) = |
|
|
||||||||||||
| partition of summantegras |
|
|
||||||||||||
|
change of variables of the first summantegras (x/r → x) |
|
|
||||||||||||
| deformation |
|
|
||||||||||||
|
case of r = 2 |
|
|
Remarkable thing
The steps from the partition through change of variables correspond to deformation of series.
This fact reminded me of the following articles.
If I illustrate the steps from the partition through change of variables, it will be as follows.
Before
After
↑ These drawings were added on February 28, 2016.
Addition
Indirect method using the equivalence of probability distributions
Notations
Let x be the amount of money in the envelope selected by you.
Let X be a random variable which take x as its value.
Let Y be a random variable which denotes the amount of money in your new envelope after switching under the condition you always switch.
Let a be the lesser amounts in the two envelopes.
Let r ( > 1) is the ratio of the greater amount to the lesser amount.
Let g(a) be the probability or probability density of the event of the pair of amount of money is (a, ra).
Let
If the distribution of amount of money is discreet,
If the distribution of amount of money is continuous,
Let P(x) be the probability or probability density of the event that
Let O(x) be the probability or probability density of the event that
Let G(x) be the probability or probability density of the event that
Let L(x) be the probability or probability density of the event that
using P the equivalence of the distribution of X and Y can be proven.
| L(x) = | g(x) + k g(x/r) |
P(x) |
| = | g(x) + k g(x/r) |
(1/2)(g(x) + kg(x/r)) |
| = | (1/2)g(x) |
| G(x) = | g(x/r) + k g((x/r)/r) |
P(x/r) |
| = | g(x/r) + k g((x/r)/r) |
(1/2)(k(g(x/r) + k2g((x/r)/r)) |
| = | (1/2)kg(x/r) |
In other words, the distribution of the amount of money before switch is same as it after switch.
So if mean values are finite they are same.
Reference
-
Chalmers, D.J. 1994.
The two-envelope paradox: A complete analysis?
-
Clark, Michael. & Shackel, Nicholas. (2000).
The Two Envelope Paradox, Mind Magazine (Vol 109.435.July 2000)
-
Norton, J.D. 1998.
When the sum of our expectations fails us: The exchange paradox.
Pacific Philosophical Quarterly 79:34–58.
-
Wagner, Carl G.(1999).
Misadventures in Conditional Expectation: The Two-Envelope Problem
Erkenntnis, Vol.51, No.2/3 (1999), pp.233–241
Return to the list of my pages written in English about the two envelopes problem