モンティ・ホール問題好きのホームページ    privacy policy

Return to the list of my pages written in English about the two envelopes problem
2017/03/02 21:18:05
First edition 2016/10/02

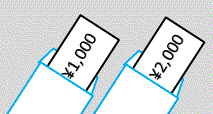An intuitive resolution of the two envelope paradox

Caution
I who am a Japanese wrote this page in English, but I am not so good at English.

I found a method which uses frequency instead of probability to prove the equivalence of the two envelopes. This method is not complete but more intuitive than standard method.

The two envelopes problem

The two envelopes problem is like this.
There are two envelopes.
An unexpected amount of money is placed in one envelope, and twice that amount is placed in another envelope.
Each expected amount of money of each envelope is equal to the mean value of the amounts of money in the two envelopes.
Therefore these envelopes are equivalent.
You chose one envelope at random.
Let x be the amount of money in your envelope.
The expected amount of money in the other envelope is (1/2)(x/2) + (1/2)(2x) = (5/4)x > x.
Therefore these envelopes are not equivalent.
<<Various description of the existence of a paradox follows.>>

Major paradoxes of the two envelopes problem.

The mathematically standard paradox (Breaking the law of total expectation)

Some people including me felt the standard paradox as follows.
Because this calculation does not depend on the amount x, anytime after choice the two envelopes are not equivalent.
Before you chose an envelope, two envelopes are equivalent.
But after choice of an envelope the equivalence is broken.
This is a paradox.

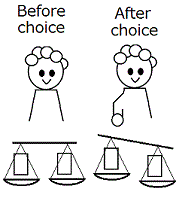
Some people including mathematicians gave the standard resolution to this mathematically standard paradox.

For reference.

Another major paradoxes

Paradox of the two envelopes which are greener than each other
Some people including me felt another paradox as follows.
Because this calculation does not depend on the envelope, so you should change your choise even if you have chosen the oposite envelope.

This means an envelope is more favorble than itself.
For resolution of this paradox, please see my page "An outline of the Two Envelopes Problem".

Paradox of the money pump
Some people including me felt another paradox as follows.
Because we can apply this calculation after change of envelopes. So if we repeat swapping, the expected amount of money in the chosen envelope will grow up in the rate 25% per every swap.

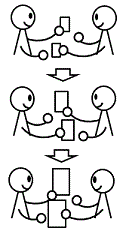
It means there is a money pump.
For resolution of this paradox, please see my page "An outline of the Two Envelopes Problem".

Paradox which was resolved by DivideThreeByTwoians
Some people who are not majority resolve another paradox as follows.
The correct expectation formula is as follows.
Let A and 2A be the smaller amount of money and the larger amount of money in the two envelopes respectively.
Then the expected values of the amounts of money in each envelopes are E = (1/2)A+ (1/2)2A.
The expectation formula "E = (1/2)(x/2) + (1/2)2x." in the two envelopes problem is wrong.
This fallacy of expectation formula is the cause of the paradox.

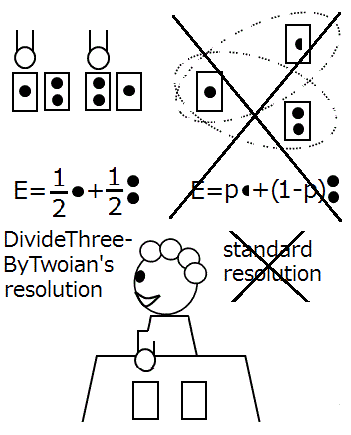
↑ This picture was added on April 23, 2016.
When I think of the people who have this opinion, I call them "DivideThreeByTwoian",  because (1/2)A + (1/2)2A = (3/2)A.
For details of this paradox, please see my page "An outline of the Two Envelopes Problem".

The standard method for resolving the standard paradox

The goal

Let X be a random variable of the amount of money in the chosen envelope.
Let Y be a random variable of the amount of money in the opposite envelope.
Let x be the amount of money in the chosen envelope.
Then it is the goal to prove E(E(X | X = x)) = E(E(Y | X = x)).

The standard methods

I think that the methods used in the following articles are standard.

An intuitive method using frequency to resolve the standard paradox

technic used

The first goal of this mthod

Let X be a random variable of the amount of money in the chosen envelope.
Let Y be a random variable of the amount of money in the opposite envelope.
Let x be the amount of money in the chosen envelope.
Let N be the number of all elements of the sample. In other words , let N be the total number of times of games.
Then it is the goal to prove that (1 / N)∑(∑X=xX) ≈ (1 / N)∑(∑X=xY).

An intuitive proof of the goal

∑(∑X=xX) contains all elements of the sample.
Therefore   ∑(∑X=xX) = ∑X

∑(∑X=xY) contains all elements of the sample.
Therefore   ∑(∑X=xY) = ∑Y

On the other hand   (1 / N)∑X ≈ (1 / N)∑Y, because N (total number of times of games) is large.
Therefore   (1 / N)∑(∑X=xX) ≈ (1 / N)∑(∑X=xY).

The second goal of this method

It is the remaining goal of this method to prove that (1 / N)∑(∑X=xX) ≈ (1 / N)∑(∑X=xY) imply that E(E(X | X = x)) = E(E(Y | X = x)).

An intuitive proof of the second goal

Let n(x) be the number of elements of the sample such that X=x.  In other words, let n(x) be the number of times of games such that the lesser amount of money is x.

(1 / N)∑(∑X=xX) ≈ (1 / N)∑(∑X=xY)
↓
(1 / N)∑(∑X=x(X - Y) ≈ 0
↓
∑(n(x) / N)(∑X=x( (X - Y) / n(x) ) ≈ 0
↓
E(E(X - Y | X = x)) = 0
↓
E(E(X | X = x)) = E(E(Y | X = x))

Example of the fact that (1 / N)∑(∑X=xX) ≈ (1 / N)∑(∑X=xY)

elements of the sample ∑X=xX ∑(∑X=xX) (1/N)∑(∑X=xX) ∑X=xY ∑(∑X=xY) (1/N)∑(∑X=xY)
chosen
amount 		opposite
amount
10 20 30 640 35.56 60 620 34.44
10 20
10 20
20 10 80 100
20 10
20 40
20 40
30 60 90 180
30 60
30 60
40 20 160 140
40 20
40 20
40 80
60 30 120 60
60 30
80 40 160 80
80 40
↑ Revised on Octoer 10, 2016.

Reference



Return to the list of my pages written in English about the two envelopes problem