トップページに戻る
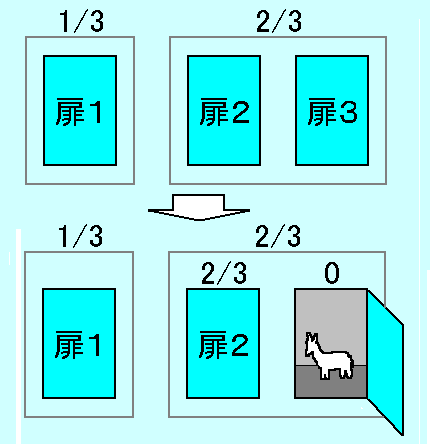
こうした説明では次のような図が使われることが多い。
筆者もこの確率継承説を思いついて自画自賛していたものだが、モンティ・ホール問題の不思議さが薄れて行くにつれてその考え方の誤りがわかるようになりました。
以下、こうした説明の例として、NHKの「2355」での説明の仕方を見てみます。
太田は、コップを変えた方がよいことを、次のように説明していた。
画面上では、田中が選ばなかった紙コップが一つのグループを形成していることを、画像合成で示していた.

①田中が選ばなかったコップたちの中に当たりがある確率が変わらない理由を何も説明していない。
②残ったコップに確率 3 / 4 が継承されると言っているが、「まさにその」コップのことを言っているのか、「残されるであろうどれかのコップ」のことを言っているのか判別できない。
これを図解すると次のようになる。
このように何も確率論的な説明がなされていないので、あたかも確率が重さのようなもので、太田が開けたコップの重さ(確率)がゼロだから、残りのコップに重さ(確率) 3 / 4 が継承されると考えているかのようである。
「太田がどれかのハズレのコップを田中に開けさせた」という事象と、
「田中が選ばなかったコップの中に当たりがある」という事象は独立である。
したがって、「田中が選ばなかったコップの中に当たりがある」という事象の、
「太田がどれかのはずれのコップを田中に開けさせた」という事象を証拠事象とする事後確率は
事前確率と一致する。
(田中が選ばなかったコップの間に対称性があると言い換えることができる)。
したがって、「太田がそれらのコップを田中に開けさせた」という事象を証拠事象とする
「田中た選ばなかったコップの中で残されたまさにそのコップが当たりだ」という事象の事後確率は、
「田中が選ばなかったコップの中に当たりがある」という事象の事後確率と一致する。
2013/08/18 14:36:35
確率継承説の間違い
モンティ・ホール問題の説明の仕方として、挑戦者が選ばなかった扉の中から選んだ扉をホストが開けるので、挑戦者が選ばなかった扉全体の確率が残った扉に継承されるという、ものがある。こうした説明では次のような図が使われることが多い。
筆者もこの確率継承説を思いついて自画自賛していたものだが、モンティ・ホール問題の不思議さが薄れて行くにつれてその考え方の誤りがわかるようになりました。
以下、こうした説明の例として、NHKの「2355」での説明の仕方を見てみます。
2355での説明
2011年7月8日23:55に放送された「23:55」の爆笑問題のコーナーで、次のようにモンティ・ホール問題が取り上げられた。田中の前に紙コップ4個が伏せられている。 太田:「ひとつの紙コップにキャンディがある」 太田:「田中が選んだ紙コップにキャンディが あればそれを食べられる」と述べて 田中に選ばせる。 田中:画面向かって左端の紙コップを選ぶ。 太田:「田中にいいことを教えて上げよう。 画面向かって右端の紙コップは空だ。 開けて見なさい」 田中:右端の紙コップを開けて、 中をカメラに向ける。 太田:「もう一ついいことを教えて上げよう。 一つ置いた紙コップも空だ。 開けてみなさい」 田中:右から3番目の紙コップを開けて、 中をカメラに向ける。 太田:「2個の紙コップが残った。 紙コップを変えてもよいがどうする?」 田中:最初に選んだ紙コップを開けて 空であることを示す。 がっかりはしていない。
太田は、コップを変えた方がよいことを、次のように説明していた。
田中が選んだ紙コップにキャンディがある確率は 1 / 4 で、田中が選ばなかった3個の紙コップの中にキャンディーがある確率は 3 / 4。 2個の紙コップがハズレだとわかっても田中が選ばなかった紙コップの中に当たりがある確率は変わらないので、残った紙コップに、確率 3 / 4 が残る。
画面上では、田中が選ばなかった紙コップが一つのグループを形成していることを、画像合成で示していた.
太田の説明の間違い
この説明にはいくつか欠陥がある。①田中が選ばなかったコップたちの中に当たりがある確率が変わらない理由を何も説明していない。
②残ったコップに確率 3 / 4 が継承されると言っているが、「まさにその」コップのことを言っているのか、「残されるであろうどれかのコップ」のことを言っているのか判別できない。
これを図解すると次のようになる。
| 田中が選んだコップ |
田中が選ばなかった |
|
|---|---|---|
|
太田が 開けさせる前 |
確率 1 / 4 |
確率 3 / 4 |
|
太田が 田中にコップを 開けさせた後 |
この中に当たりがある確率は 1 / 4 で変わらない。 何故? |
この中に当たりがある確率は 3 / 4 で変わらない。 何故? |
|
確率 1 / 4 |
残ったコップに確率 3 / 4 が継承される まさにこのコップのことか? それとも残されたコップ一般のことか? |
このように何も確率論的な説明がなされていないので、あたかも確率が重さのようなもので、太田が開けたコップの重さ(確率)がゼロだから、残りのコップに重さ(確率) 3 / 4 が継承されると考えているかのようである。
あるべき説明の姿
「まさにそのコップに確率 3 / 4 が継承される」理由を、まっとうな確率論で説明するためには、次のように、2段階で説明することが必要である。第1段階
標準仮定の下では、「太田がどれかのハズレのコップを田中に開けさせた」という事象と、
「田中が選ばなかったコップの中に当たりがある」という事象は独立である。
したがって、「田中が選ばなかったコップの中に当たりがある」という事象の、
「太田がどれかのはずれのコップを田中に開けさせた」という事象を証拠事象とする事後確率は
事前確率と一致する。
第2段階
標準仮定の下では、田中が選んだコップが当たりのときに、太田が田中に開けさせるコップの選び方に偏りがない。(田中が選ばなかったコップの間に対称性があると言い換えることができる)。
したがって、「太田がそれらのコップを田中に開けさせた」という事象を証拠事象とする
「田中た選ばなかったコップの中で残されたまさにそのコップが当たりだ」という事象の事後確率は、
「田中が選ばなかったコップの中に当たりがある」という事象の事後確率と一致する。
確率継承説が間違いであることを一発で論証
次のように考えると、確率継承説が間違いであることがすぐに分る。(2012/01/14に気付きました)こうした確率継承説では、挑戦者が選ばなかった扉の中から、ホストが あてずっぽう に扉を開けたケースも含んでいる。
2355で言えば、太田が田中に あてずっぽうで 開けるコップを指示した場合も含んでいる。
しかし、 あてずっぽう で開けた場合には、残った扉やコップが当たりである確率は 1 / 2 になってしまって、確率継承説の予想と反してしまう。
もう一つ、次のように考えると、確率継承説が間違いであることがすぐに分る。(2013/06/01に気付きました)
こうした確率継承説では、挑戦者が選んだ扉が当たりのときに、ホストが 特定の 扉を開けたがるケースも含んでいる。
2355で言えば、太田が田中に 好んで 両端のコップを開けるように指示した場合も含んでいる。
しかし、 好んで 両端のコップを開けた場合には、残った扉やコップが当たりである確率は 1 / 2 になってしまって、確率継承説の予想と反してしまう。
確率継承説を数式で書くだけでも間違いがわかる
次のように考えると、確率継承説が間違いであることがすぐに分る。(2013/07/04 に気付きました)確率継承説での説明は、次のような数式を立てていることになる。
|
田中が選んだコップはコップ1 で、太田が田中に開けさせたコップはコップ2, 4 だとする。
太田が田中にコップ2, 4 を開けさせる前 太田が田中にコップ2, 4 を開けさせた後 したがって、 太田が田中にコップ2, 4 を開けさせた後 つまり、 |
この数式のおかしな点は、開けたコップを特定しないで計算した確率
用語解説
-
標準仮定
モンティ・ホール問題を数学的に解くためには問題文に明示的に書かれていない条件を仮定する必要がある。
標準仮定はそうした仮定の一つであり、次のような内容となっている。
①当たり扉はランダムかつ等確率に設定される
②ホストは挑戦者の選んだ扉を開けない
③ホストは必ず残りの扉を一枚開ける
④ホストはハズレの扉しか開けない
⑤ホストは挑戦者の選んだ扉が当たりのとき、ハズレ扉をランダムかつ等確率に選んで開ける
⑥ホストは扉を開けた後に必ずswitchの機会を挑戦者に与える
「標準仮定」(the standard assumptions)とは Wikipedia(英語版)の "Monty Hall problem"の記事で導入された言葉である。
トップページに戻る