モンティ・ホール問題好きのホームページ    privacy policy

Return to the list of my pages written in English about the two envelopes problem
2025/09/19 14:53:47
First edition 2025/09/19

New outline of the Two Envelopes Problem


※This page is an easier-to-read version made of essence of the page titled "An outline of the Two Envelopes Problem" which I made many additions and revisions to since 2015 and which has become difficult to read.
※As result, many parts in this page have addition date or revised date that are earlier than the first edition of this page.



Skip to Contents

Lead section

There are two indistinguishable envelopes containing money, one containing twice the amount of the other. One of the envelopes was then chosen at random and given to you.  When you calculate the expected value of the gain by the exchange envelopes using the relation of the amount in the envelope you were given to the amount in the other envelope, you notice that the other envelope is more preferable.  The Two Envelope Problem is a problem that demands you to solve a paradox in which the equality of two envelopes is destroyed as soon as one of the envelopes is given to you.  There are many different types of questions and no single interpretation for them, so there are a variety of answers flying around.  And what's worse is that time is wasted on pointless arguments between people with different interpretations.

Contents

Common Structure and Variations of Problem Statements

Common Structure

The problem statements for the two envelopes problem consist of three parts: 1) game setting, 2) expected value calculation, and 3) paradox.

The part of game setting describes the following:
The part of expected value calculation describes the following:
Various paradoxes are described in the paradox part.
For example:

Major variations of the problem statements

Variations on number of players
Variations on exchange opportunities

Variations on the explanation of how the expected value is calculated

Variations on the paradox presented

Important examples of problem statements

Earliest published problem statement

I believe Zabell, S. (1988) is the earliest reference that presented the two envelopes problem

Below is a summary I have made of the program statement presented in it.
A, B and C play a game.  C places an unspecified amount of money x in one envelope and a amount 2x in another envelope.  One envelope is handed to A, the other to B.  A opens his envelope and see $10 in it.
A reasons as follows:
"There is a 50-50 chance that B's envelope contains $5. and B's envelope contains $20.  If I exchange envelopes, my expected holdings will be (1/2)$5 + (1/2)$20 = $12.50, $2.50 in excess of my present holdings.
When A offers to exchange envelopes, B agrees since B has already similarly reasoned.
This problem statement has the following characteristics.

Early problem statement published by philosophers

I believe Jackson, F., Menzies, P., & Oppy, G. (1994). is the earliest reference that presented the two envelopes problem.

Below is a summary I have made of the program statement presented in it.
A person is offered a choice between two envelopes, A and B.
She is told that one contains twice as much money as the other with no information as to which one that is. She chooses A but before opening A she think and get a line of reasoning which suggests that she should have taken B instead.
Suppose that the amount of money in A is $x.
Then B either contains $2x or $0.5x with same possibility.
Hence the expected value of taking B is 0.5 x $2x + 0.5 x $0.5x = $1.25x, a gain of $0.25x.
This conclusion cannot be right because:
For the situation between A and B is symmetrical, the merely choosing of A cannot give a reason that she ought to have picked up B instead.
Whether she chosen A or B initially the same reasoning would suggest that she made the wrong choice!
This problem statement has the following characteristics

Problem statement in that expected value calculation is explained using words only

The lead section of the revision at 03:24, 21 June 2016 of the English language Wikipedia article "Two envelopes problem" contains a summary of the problem statement, in which the following expected value calculation is described.
…… It seems obvious that there is no point in switching envelopes as the situation is symmetric. However, because you stand to gain twice as much money if you switch while risking only a loss of half of what you currently have, it is possible to argue that it is more beneficial to switch. The problem is to show what is wrong with this argument.
This problem statement has the following characteristics

Variations in interpretation of the problem

Interpretation imagining two pairs of amounts



With two pairs of amounts as the range of consideration, the expected value is calculated conditional on the amount of money in the selected envelope. The context of the game setting and context of the expectation calculation part are different.

When the problem statement uses a specific amount of money, as in Zabell, S. (1988)'s problem statement, this interpretation is the only possible one.
When the problem statement uses a character expression, as in Jackson, F., Menzies, P., & Oppy, G. (1994). , this interpretation may is one of the possibilities.

Famous examples
Papers by mathematicians or philosophers
Zabell, S. (1988)
Nalebuff, Barry.(1989)
Christensen, R; Utts, J (1992),
Jackson, F., Menzies, P., & Oppy, G. (1994).
Chalmers, D.J.
World's oldest Wikipedia article on the two envelopes problem
The English language Wikipedia article "Envelope paradox" (Revision at 10:55, 26 August 2004) (How to read it)
Wikipedia article as of 2025
Section "Bayesian resolutions" of the English language Wikipedia article "Two Envelopes problem" (Revision at 12:44, 22 April 2025)
The German language Wikipedia article "Umtauschparadoxon" (bearbeitet am 29. November 2024 um 10:56)
et cetera

Interpretation imagining one pair of amounts



With one pair of amounts as the range of consideration, the expected value is calculated conditional on the lesser amount of money in the two envelopes. The context does not change through the game setting and the expectation calculation part.

When the problem statement uses a character expression, as in Jackson, F., Menzies, P., & Oppy, G. (1994). , this interpretation may is one of the possibilities.

Famous examples
Papers by philosophers
Priest, G., & Restall, G. (2003).
The earliest Wikipedia article introducing this kind of interpretation
The English language Wikipedia article "Envelope paradox" (Revision at 01:47, 7 June 2005) (How to read it)
Wikipedia article as of 2025
Section "Example resolution" of the English language Wikipedia article "Two Envelopes problem" (Revision at 12:44, 22 April 2025)
The French language Wikipedia article "Paradoxe des deux enveloppes" (en date du 27 décembre 2023 à 17:21)
et cetera

Interpretation imagining all pairs of amounts

With all possible pairs of amounts as the range of consideration, the expected value is calculated using mean value of the lesser amount and mean value of the greater amount. in the two envelopes. The context of the game setting and the context of the expectation calculation part are different.

When the problem statement uses words only, as in the lead section of the revision at 03:24, 21 June 2016 of the English language Wikipedia article "Two envelopes problem", this interpretation may is one of the possibilities.
When the problem statement uses a character expression, as in Jackson, F., Menzies, P., & Oppy, G. (1994). , this interpretation is not possible.

Examples
Writings by mathematicians
Jeffrey, R. (2004)
The following formula is presented as the wrong calculation.
… As you think Y equally likely to be .5X or 2X, ex(Y) will be .5ex(.5X) + .5ex(2X) = 1.25ex(X) …
Personal examples
My experiene
I thought the problem without seeing written problem text, as follows.
I imagined the whole possible amounts in the chosen envelope.
    ↓
I thought it equally likely will be halved or doubled.
    ↓
In my mind the following formula appers without awareness.
ex(Y) = .5 (.5 ex(X)) + .5 (2 ex(X)) = 1.25ex(X).

Each solution corresponding to each interpretation

Solution noticing probability illusion

This solution is for the interpretation imagining two pairs of amounts. And the claims of it are as follows. I wrote detail About this solution I wrote details in the section "Fundamental mathematical theories" of the page "An outline of the Two Envelopes Problem". And I hope you will read that.

In my web page "Interesting web pages about the Two Envelopes Problem" I wrote a list of easy-to-understand web pages that explain the correct probabilities.

Solution exposing tricks which make us tricked by the calculation

This solution is for the interpretation imagining one pair of amounts. The proponents of this solution created diagnostic argument to prove the flaws in the faulty expected value formula.
They appear to have tried to uncover the tricks hidden behind the formula that uses the amount in the selected envelope to calculate the expected value of the amount in the other envelope. They then created diagnostic argument based on tricks they discovered.
The tricks that they revealed from the fallacious formula "(1/2)(x/2) + (1/2)2x" may be as follows.
They then created the following diagnostic argument based on the above tricks. This solution advocator seamed think that the context does not change through the game setting and the expectation calculation part.
I think there is no doubt in their minds that the correct expected value calculation is to calculate the average of the amounts in the pair of amounts. Therefore they doubted the combination of x/2 and 2x in the fallacious expectation formula.

Solution that noticing that the conditions of conditional expected values are ignored

This solution is for the interpretation imagining all pairs of amounts.

Solution noticing the "discharge fallacy" (written in Jeffrey, R. (2004))
My solution

Mystery that almost people cling to a single interpretation

Each person discussing the two envelope problem has their favorite interpretation and dislikes or abhors other interpretations. To explain this mystery, I came up with the following hypothesis:
Fixation on the experienced Eureka effect
Human who have experienced eureka effect become not able to accept the another solution.
Analysis method preference
There are people who are good at evaluating the suspiciousness of each part of a fallacious formula, and there are people who are good at finding errors in the reasoning process that leads to the fallacious formula.
People have different tolerances for uncertainty of the amount in the selected envelope.
When recalling the amount of money in a selected envelope, no one can recall both a fixed and a variable image. In other words, some people cannot accept that the amount in the handed envelope can be A or 2A, while others cannot accept that the amount in an envelope they have not yet checked is fixed at X.

Mathematics in the interpretation of imagining two pairs of amounts

Expectation formula – Case of discrete distribution –

Let g(m) be the probability that m is the lesser amount.
Let X be the random variable of the amount of money in the chosen envelope.
Let Y be the random variable of the amount of money in the other envelope.
Then expected winning from a trade are
E(Y|X=x) = ( g(x/2) / (g(x) + g(x/2)) )(x/2) + ( g(x) / (g(x) + g(x/2)) )2x.
For reference.

Expectation formula – Case of continuous distribution –

Let g(m) be the probability density function that m is the lesser amount.
Let X be the random amount of money in chosen envelope.
Let Y be the random amount of money in the other envelope.
Then the random variable of the conditional expected value of the other amount on the condition that X is the chosen amount is as follows.
E(Y|X) = (g(X) / (g(X)+(1/2)g(X/2)) )2X + ((1/2)g(X/2) / (g(X)+(1/2)g(X/2)) )(X/2).
↑ Revised on May 3, 2018, November 4, 2018.
For reference. The above literatures presented various methods to calculate the probability density function f(b) of the greater amount b using the probability density function g(a) of the lesser amount a, as follows.

Theories for the expected value formula of amount in the other envelope

Not necessarily 1/2

(Added on April 6, 2016. Revised on September 4, 2016.)
Let X be the amount of money in the chosen envelope.
Then there is a prior distribution such that
P(X is lower | X=x) ≠ 1/2 and P(X is greater | X=x) ≠ 1/2 for some x.
Popular proof
Let M be the max of possible amount of money.
Let x be the amount of money in the chosen envelope.
Then if x > M/3, the amount of money in the opposite envelope can not be 2x, in other words the probability is zero or undefined.

For reference.

Not always 1/2

Let X be the amount of money in the chosen envelope.
Then there is no prior distribution such that
P(X is lower | X=x) = P(X is greater | X=x) = 1/2 for all x.
Proof by Zabell, S. (1988).
(Added on November 6, 2016)
If P(X is lower | X=x) = P(X is greater | X=x) = 1/2 for all x, then
either the interval [1,2) and R+ would have zero probability mass, or [1, 2) and R+ would have infinite probability mass.
In either case the probability distribution cannot be proper.
Popular proof for discrete distribution of amounts of money.
If P(X is lower | X=x) = P(X is greater | X=x) = 1/2 for all x, then
there are amount a such that sum of P(X=2n × a) diverges, and the probability distribution cannot be proper.
(↑ Revised on April 7, 2016 and April 24, 2016)
One more proof for discrete distribution of amounts of money.
Let g(x) be the probability of the event "The pair of amounts of money is x and 2x".
Then limx→∞ g(x) = 0.
Therefore for some amount of money x, g(x/2) > g(x).
For reference.
• A blog page "The Universe of Discourse : The envelope paradox".
Is this proof by me for continuous distribution of amounts of money correct?
Let g(x) be the probability density function of the event "The pair of amounts of money is x and 2x".
If P(X is lower | X=x) = P(X is greater | X=x) = 1/2 for all x, then g(2x) = 2g(x) for all x.
Let P(n) = P(2n ≤ x ≤ 2n + 1) for natural number n, then P(n) = 2nP(0).
Therefore sum of P(n) diverges, and the probability distribution cannot be proper.

Switching is not always advantageous

Let X be the random amount of money in chosen envelope.
Let Y be the random amount of money in the other envelope.
Then if the prior distribution has a finite mean, then it is false that E(Y|X=x) > x for all x.
(↑ Revised on March 29, 2015)
 For reference.

Two envelopes are not always equivalent

Let X be the random amount of money in chosen envelope.
Let Y be the random amount of money in the other envelope.
Then for some x, E(Y|X=x) ≠ x.
(↑ Added on August 8, 2015)
 For reference.

Switching is not always non-advantageous

(Added on August 15, 2015. The title was revised on March 3, 2019)
For any probability distribution, for at least one value of x, E(Y|X=x) > x.
For reference.

Mean values of conditional expectations of the amounts of money in each envelope are same

This paragraph was revised on August 22, 2015, February 14, 2016, March 7, 2016 and March 20, 2016.
Let X, Y be the random variables which denote the amount of money in the chosen envelope and the other envelope respectively. And let x be the amount of money in the chosen envelope. Then E[E(X|X)] = E[E(Y|X)].
(↑ Revised on June 21, 2016.)
 For reference. I also wrote some explanations on February 2016.
Please see a companion page "Two methods for the proof of the equivalence of the envelopes of the two envelopes problem".

In 2016, I found very easy proof for discrete distributions. 

Let z be an amount of money in the chosen envelope.
Consider a sub probability space which is as follows.
  • For all integer i, it contains event that the chosen amount is 2ix.
  • In this sub probability space, g(x) is the probability that the lesser amount is x.
Let denote 2iz by zi.
Let denote g(zi) by gi.
Then E(Y|X=zi) = (gi-1 zi-1 + gi zi+1) / (gi-1 + gi).
And P(X=zi) = (1/2)(gi-1 + gi).
Then we can show that E[E(X|X)] = E[E(Y|X)] as follows..
 
 E[E(Y|X)] - E[E(X|X)]] = E[E(Y - X| X)] · · · 1
= ∑ ((gi-1 zi-1 + gi zi+1) - (gi-1 zi + gi zi))/ 2 · · · 2
= ∑ (gi-1 (zi-1 - zi) /2 + ∑ (gi zi+1 - gi zi))/ 2 · · · 3
= - ∑ (gi-1 (zi-1) /2 + ∑ (gi zi)/ 2 · · · 4
= 0 · · · 5


I expect that this drawing help us to understand the following calculation which had been done by Chalmers.
(↓ corresponding row number column was added on 25,2017.)
The final calculation in Chalmers, D.J. 1994 .
corresponding row number
in the above calculation
E(K-A) = integral[0,infinity] h(x) (E(B|A=x) - x) dx · · · 1
= integral[0,infinity] (2g(x) + g(x/2))/4 .
((2x.2g(x) + x/2.g(x/2))/(2g(x)+g(x/2)) - x) dx		 · · · 2
= integral[0,infinity] (2xg(x) - x/2 . g(x/2))/4 dx · · · if anything, 3
= (integral[0,infinity] 2xg(x)dx -
integral[0,infinity] 2yg(y)dy) /4		 · · · 4
= 0. · · · 5

Related topics

Followings are important topics other than the above. They are which I wrote on the page "An outline of the Two Envelopes Problem" which is the source of this page.

Paradoxical distributions which have infinite mean value

On March 10, 2019, this title was revised.

paradoxical distribution

If infinite mean value is allowed, there can be "Paradoxical distributions" that switching the envelopes is always advantageous for all amount of money in the chosen envelope.
Following example is most famous among such distributions.

pair of amounts probability
20 and 21 (2/3)0 / 3
21 and 22 (2/3)1 / 3
·
·
· 		·
·
·
2n and 2n+1 (2/3)n / 3
·
·
· 		·
·
·

For reference. In addition to the paradoxical discrete probability distribution, continuous probability distribution was also discussed in some of the above literatures.
For example, a probability density function "f(s)=1/(s+1)2 for s > 0" was presented in Broome,John.(1995).
(↑ Added on July 22, 2018)

Addition: (Added on September 15, 2019)
The most famous paradoxical distribution above is a special case of the following distributions.
Let r denote a number where 0 < r < 1.
Let n denote a natural number where n ≥ 0 and let (2n, 2n+1) be a pair of amounts of money placed in the two envelopes.
Let X and Y be random variables representing the amounts of money in the chosen envelope and the other envelope respectively.
And consider a probability distribution that the probability of (2n, 2n+1) is rn(1-r).
Then :
  • If r < 1/2, E(X) converges and E(X) = E(Y). (Not paradoxical)
  • If r = 1/2, E(X) diverges and E(Y|X) = E(X|X) for X ≠ 20. (The other envelope is almost always as favorable as the chosen envelope)
  • If r > 1/2, E(X) diverges and E(Y|X) > E(X|X). (Paradoxical distribution)

Paradox about the equivalence of the two envelopes on the paradoxical distribution

This paragraph was added on December 19, 2017.

There is no wonder even if the other envelope is more favorable for an amount of money of the chosen envelope.
But it is paradoxical that the other envelope is always more favorable for any amount of money of the chosen envelope.

Randomized switching

This paragraph was added on September 19, 2015.

If we can play opened version game repeatedly, which is the best strategy?

Some mathematicians study the strategies to earn more on average than the strategy not to exchange any time.
They take the condition that the distribution of the amount of money is unknown.
And they study how to decide depending on the amount of the revealed money.
Strategies which use random number are called "Randomized switching".

For reference.

An experiment

On July 12, 2015, referring to the article by Emin Martinian, I tried to see the effect of "randomized switching", and got the following result.
Condition of the experiment
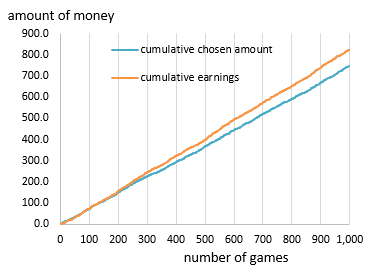
  • Amounts of money have double-precision floating-point values.
  • The lesser amount uniformly distributes between 0.0 and 1.0.
  • For the chosen amount Y, the decision to switch will be made with a probability Exp(-Y / 2).
Method
 I used Excel.

Result

An explanation

On July 15, 2016, referring to Ross, S. M., Christensen R. and Utts, J.(1994)., I created a simple explanation.
Let g(x) be a function which has the following characteristic.
If b > a,   0 < g(b) < g(a) < 1.
And let y be the amount of money in the chosen envelope.
And let S1 be a strategy to exchange in probability g(y), and let S2 be a strategy not to exchange
Then S1 will make more earnings than S2.

Why?

Let's think of a pair of amounts of money (a, 2a).
Then g(2a) < g(a).
It means that under the strategy S1, the probability to get the greater amount is (1/2) (g(a) + (1 - g(2a)). It is larger than 1/2 which is the probability under the strategy S2. (← Revised on January 5, 2020)
( For detail, please read "An alternative randomized solution" written in the section "Randomized solutions" of the English language Wikipedia article "Two envelopes problem" (Revision at 22:46, 28 December 2019). ) (← Added on January 5, 2020)
Since this argument holds for any pairs of amounts, you can expect that the strategy S1 will give you more gain. (← Added on January 5, 2020)
I had applied this explanation to the above experiment.
g(a) = Exp(-a / 2)   and   g(2a) = Exp(-2a / 2).
∴ g(2a) = g(a)2.
g(2a) < g(a)   because   g(a) < 1. (← Revised on July 1, 2017.)
 

More than one English language Wikipedia article about the two envelopes problem

As of June 16, 2019, the English language Wikipedia has the following articles about the two envelopes problem.
How to read an article which is redirected to the article "Two envelopes problem"
Example: Case of "Envelope paradox"
FirstOpen a page of the English language Wikipedia.
Second  Enter "Envelope paradox" as the search key word, and click the search button.
ThirdIf the article "Two envelopes problem" is shown, click the link on the line "(Redirected from Envelope paradox)".
FourthIf the article "Envelope paradox" is shown click the link "View history".

How to read all articles redirected to the article "Two envelopes problem"
FirstOpen the page of the article "Two envelopes problem" of the English language Wikipedia.
Second  Click the link "What links here" on the left side bar.
ThirdIf you see a page titled "Pages that link to 'Two envelopes problem'", search the links labeled "redirect page" on the page.
FourthClick the searched link.
FifthIf a redirected page is shown, click the link "View history".


Reference

Terms



Return to the list of my pages written in English about the two envelopes problem