トップページに戻る

モンティ・ホール問題はベイズの定理の応用問題なのか？

「モンティ・ホール問題はベイズの定理の応用問題だ」という考え方は、ちょっとひっかかります。
このページではモンティ・ホール問題にベイズ推定の公式を応用するやり方とベイズの定理を直接応用するやり方などを比較してみました。

このページでの決め事

前提条件

• 余計な議論に迷い込まないように、標準仮定を前提とします。
  標準仮定については「わかるモンティ・ホール問題」というページの「標準仮定」というサブページで解説しています。
• 問題のとらえ方として、「ホストが開けた扉を特定して、 残った二つの扉それぞれが当たりである確率を求めようとする」とらえ方を採用します。
  このとらえ方については「わかるモンティ・ホール問題」というページの「問題のとらえ方」というサブページで解説しています。
• 挑戦者が 1番目の扉を選び、ホストが 3番目の扉を開けるというおなじみの条件で 2番目の扉が当たりである条件付き確率を計算します。

使用する記号

数学公式を表すために次のような記号を使います。

• ev(・・・) で・・・が成立する事象を表します。例えば ev(扉1当たり) で扉1が当たりの事象を表します。
• P(・・・）で事象・・・の確率を表します。例えば P(ev(扉1当たり)) = 1/3 となります。
• P(・・・|＋＋＋）で事象＋＋＋を条件とする事象・・・の条件付き確率を表します。例えば P(ev(扉3開けた) | ev(扉1当たり)) = 1/2 となります。

モンティ・ホール問題をベイズ推定でよく使う公式で解く方法

この方法はモンティ・ホール問題を数学公式で解く場合、もっともポピュラーな方法だと思います。
私はこの方法を「ベイズ推定でよく使う公式」による方法と呼んでいます。 (← 2020/06/11 追加)

Wikipedia ではベイズ推定でよく使う公式がベイズの定理の応用として扱われている

英語販 Wikipedia の記事 "Bayesian inference" の 22:17, 15 May 2004 のリビジョンで初めてベイズ推定でよく使う公式と同じ計算方法が使われました。そのとき、ベイズの定理は公式の形で提示され、ベイズ推定でよく使う計算方法は公式でなく具体的な計算例として提示されました。

日本語版 Wikipedia の記事 「ベイズ推定」 の2006年7月4日10:08 の編集で初めてベイズ推定でよく使う公式が提示されましたが、ベイズの定理を先に表示してから、その変形として提示されました。

英語販 Wikipedia の記事 "Bayesian inference" の16:01, 26 February 2012 のリビジョンから、ベイズ推定でよく使う公式が "Inference over exclusive and exhaustive possibilities" という特別なケースの公式として取り扱われるようになりました。

しかし、歴史的には、ベイズ推定でよく使う公式の方が先ではないか？

間違っているかも知れませんが、ベイズ牧師が使ったのはベイズの定理ではなく、ベイズ推定でよく使う公式の方だと思います。つまり、ベイズ推定でよく使う公式はベイズの定理なしで編み出されたのだと、私は想像しています。
さらに、条件付き確率の定義の分母と分子を同時に書き換えるとベイズ推定でよく使う公式になるので、ベイズの定理は必要ありません。

モンティ・ホール問題を解くとき、ベイズ推定でよく使う公式を無意識に使うことが多い

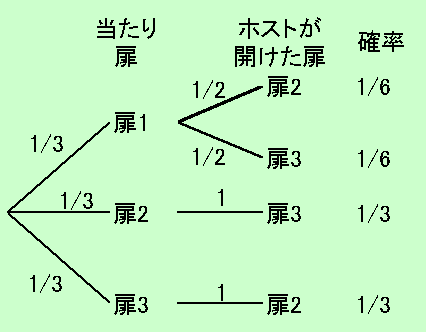
扉1が選ばれ、扉3が開けられたという条件で扉2が当たりである条件付き確率を樹形図で求めることがあります。そこで使われている計算方法はベイズ推定でよく使う公式に他なりません。
例：


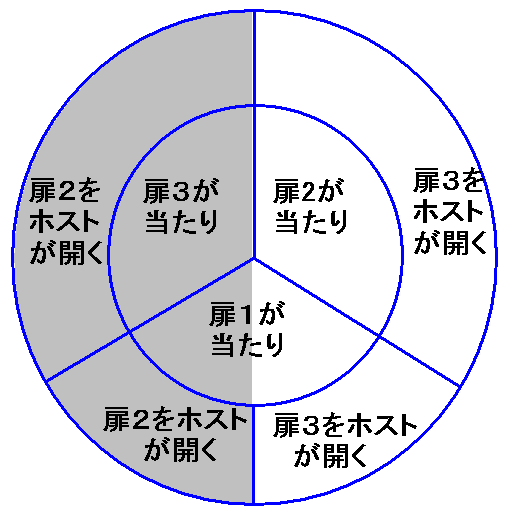
標本空間を表す四角形や円形を階層的に分割する方法があります。面積や角度が確率でなく、確からしさ（オッズ）を表している点がベイズ推定でよく使う公式と異なりますが、本質的には同一でしょう。
例：市川 伸一, 下條 信輔. (2010).で紹介されている「ルーレット表現」

条件付き確率の定義から直接計算する方法

この方法で計算するためには分子をベイズの定理で解く方法の分子に書き換える必要があるので、ベイズの定理で直接計算する方法と違いがありません。
それはともかく、この方法はあまり見かけません。

ベイズの定理で直接計算する方法

この方法には、次の下記の問題点があると思います。

却って計算が複雑になっている

この方法で分母を直接計算するのであれば、どの扉が当たりかという事象と、どの扉を開けるかという事象の間の独立性を証明するか、扉2と扉3の間の対称性から、それらを開ける確率がそれぞれ 1/2 であることを述べるかしなければなりません。

あるいは分母を、ベイズ推定でよく使う公式の分母に書き換えて計算するのであれば、次を証明しなければなりません。 (← 2020/06/11 修正)

結論

モンティ・ホール問題をベイズ推定でよく使う公式で解くと結果的にベイズの定理を応用したことになるのかも知れません。
しかし多くの場合、ベイズの定理を使っている意識はないので、わざわざ言うほどのものではないと思います。
もしかしたら、「ベイズの定理の応用だ」という説明は知ったかぶりのデマかも知れません。 (← 2020/06/11 追加)
いずれにせよ、モンティ・ホール問題を解くとき、ベイズの定理を旗印にして解くことは、数学者による論文を除いて、ほとんど見かけません。

参考文献

• 市川 伸一, 下條 信輔. (2010).
  3囚人問題研究の展開と意義をふり返って . 認知心理学研究. 2010, Vol. 7, No. 2, p.137-145 .
  

トップページに戻る

---