トップページに戻る

対戦型モンティ・ホール問題はなぜ正答率が高いのか

 このページは 2013/01/05 に修正と加筆を行いました。
 このページは 2013/05/13 にも修正と加筆を行いました。

対戦型と標準型

Tubau, E. & Alonson, D. (2003). の実験では、モンティ・ホール問題の問題文を何種類か使っているが、それらの問題文は大きく分類すると、標準型モンティ・ホール問題と対戦型モンティ・ホール問題の 2つに分類できる。

標準型：

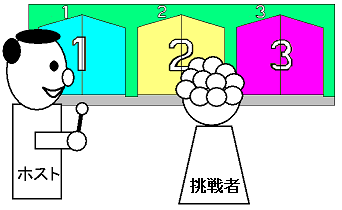
扉が3枚あって、挑戦者もホストも扉の同じ側にいる形式で、ホストは挑戦者の目の前では扉の中を覗いたりしない。
挑戦者の意識とホストの意識の差をイメージすることが困難。
モンティ・ホール問題を有名にした 世界的モンティ・ホール問題 がこの形式の代表。

対戦型：

最初に１枚のカードを選ぶ者と、残りのカードを2枚手にする者が相対して行う形式で、1枚持っている方はカードの表を見せてもらえないが、2枚持っている方は表を見ることができる。
1枚持っている者と 2枚持っている者の意識の違いをイメージすることが容易。
カードの代わりにカップや封筒を使ってもよい。.


2010年1月３日の平成教育委員会で出された、お年玉のポチ袋３つを使った問題もこの形式で、たけし先生は 2つのポチ袋の中を見てから空の袋を開けているらしい。 （Yahoo!知恵袋 などでの Q∧A から判断）

Tubau, E. & Alonson, D. (2003). の対戦型のモンティ・ホール問題は裏を見ただけでは区別できないトランプを使っているので、厳密にはモンティ・ホール問題ではなく、「扉を区別できないモンティ・ホール問題もどき」と呼ぶべきである。
数学的なとらえ方を非条件付確率の問題設定に限定して議論するのであれば、モンティ・ホール問題に数えてよいかも知れない。
通常の人間は非条件付確率の問題設定をとることが困難なので、 （少なくとも筆者がモンティ・ホール問題の初心者であった頃はそうだったので） 対戦型のモンティ・ホール問題を心理学の実験材料とするということは、 不特定事象による条件付確率あるいは事後確率の問題設定  、もしくは 非条件付確率の問題設定 に誘導する効果を実験していることになる。

De Neys, W. & Vershueren, N. (2006). の対戦型のモンティ・ホール問題ではカップをテーブルか何かの上にならべているようなので、並んだ順でカップを区別することができそうである。 特定事象による条件付確率あるいは事後確率の問題設定 をとることができるかも知れない。

対戦型にすることによって形成されるメンタルモデル

モンティ・ホール問題に出てくるゲームを対戦型にすると正答率が上がるという現象が、下記の認知心理学的研究で明らかになっている。

Tubau, E. & Alonson, D. (2003).
De Neys, W. & Vershueren, N. (2006).

対戦型にすると確率の問題構造を正しく写したメンタルモデルができやすいから正答率が上がるのだという説がある。

それはそうに違いない。

しかし、そのメンタルモデルは

特定事象による条件付確率あるいは事後確率の問題設定

不特定事象による条件付確率あるいは事後確率の問題設定

非条件付確率の問題設定

のいずれであろうか。
あるいは、 確率継承説 のように数学的にインチキでありながらも正解を導くメンタルモデルであろうか

あるいは、 Shimojo,S.,& Ichikawa,S.(1989). に書かれている　“Irrelevant, therefore invariant theorem” や、 Falk, R. (1992). に書かれている "no-news, no-change" belief のようなヒューリスティクが誘導されるようになるのであろうか？

 

特定事象による条件付確率あるいは事後確率の問題設定 のメンタルモデル

仮に 特定事象による条件付確率あるいは事後確率の問題設定 のメンタルモデルができたとしたら、メンタルモデルの構造がどのようなものであれ、下図のような確率が異なるケースを含む場合分けになるはずである。

カード 3 が 当たり	カード 1 が 当たり		カード 2 が 当たり
カード 1 を 選択	カード 1 を 選択		カード 1 を 選択
カード 2 を見せる	カード 2 を見せる	カード 3 を見せる	カード 3 を見せる

 

不特定事象による条件付確率あるいは事後確率の問題設定  のメンタルモデル

対戦型にすることで、下図のようなメンタルモデルが出来上がったと考えると、 不特定事象による条件付確率あるいは事後確率の問題設定  のメンタルモデルになる。

カードを 2枚持つ側の視点で作られているこどがこのモデルの特徴である。

1枚持つ側	2枚持つ側
2枚持っている側からは見えない

このように 対戦者別の 2重構成のメンタルモデルになっているのではないかと、私は考える。
日常的な確率概念は数学の確率概念とはまったく別物なので、このようなことがあってもおかしくない。 

非条件付確率の問題設定 のメンタルモデル

非条件付確率の問題設定 のメンタルモデルが Johnson-Laird, P. N., Legrenzi, P., Girotto, V., Legrenzi, M. S., & Caverni, J.-P. (1999). に書かれているので、それを参考にすると次のようになる。

カード1 選んだカード	カード2	カード3
当り	ハズレ 見せる	ハズレ 見せない
当り	ハズレ 見せない	ハズレ 見せる
ハズレ	当り	ハズレ 見せる
ハズレ	当り	ハズレ 見せる
ハズレ	ハズレ 見せる	当り
ハズレ	ハズレ 見せる	当り

これは 特定事象による条件付確率あるいは事後確率の問題設定 のメンタルモデルとしてとらえることも可能であるが、Johnson-Laird, P. N., Legrenzi, P., Girotto, V., Legrenzi, M. S., & Caverni, J.-P. (1999). では非条件付確率の問題設定 のメンタルモデルとして考察している。
見せるカードを区別してモデルを作る必要性から、カード1 がハズレでカード2 が当りの行を 2行に増やしたり、カード1 がハズレでカード3 が当りの行を 2行に増やすといった トリック を使っているので、このようなメンタルモデルが人間の頭の中で形成されるとは考えづらい。

このメンタルモデルを加工して、行をコピーするという トリック を使わないメンタルモデルを求めると、次のように 特定事象による条件付確率あるいは事後確率の問題設定 のメンタルモデルと変わらなくなってしまい、 確からしさが異なる行が混在して、 頭の中で形成されるメンタルモデルには相応しくない。

カード1 選んだカード	カード2	カード3
当り	ハズレ 見せる	ハズレ 見せない
	ハズレ 見せない	ハズレ 見せる
ハズレ	当り	ハズレ 見せる
ハズレ	ハズレ 見せる	当り

Tubau, E. & Alonson, D. (2003).  では、下図のような見せるカードを区別しないケースを含むメンタルモデルを想定しているようだ。

	カード1 選んだカード	カード2	カード3	見せるカード
可能性1	当り	ハズレ	ハズレ	カード2 かカード3
可能性2	ハズレ	当り	ハズレ	カード2
可能性3	ハズレ	ハズレ	当り	カード3

 

確率継承説 のメンタルモデル

対戦型にすると 2枚持つ者の手の中のカードの当り易さが手の中に保存されて、 結果として残った1枚の当り易さを 2倍にするというメンタルモデルができやすそうである。

それを図にすると次のようになる。
図の中の■はカードの当り易さを表します。

	1枚持つ者の手の中	2枚持つ者の手の中
ハズレが1枚 見せられる前	■ カード	■ ■ カード カード
ハズレが1枚 見せられた後	■ カード	■ ■ カード カード

 

"Irrelevant, therefore invariant theorem" ヒューリスティク

３囚人問題に関する心理学実験で、看守が処刑される囚人の名をあげるという証拠事象を考慮しないで、事前確率をそのまま結果の確率として計算する人も、数は少ないがいることがわかっている。
こういう人の認知メカニズムについては、次のような説がある。

Shimojo,S.,& Ichikawa,S.(1989). に書かれている "Irrelevant, therefore invariant theorem" という説

Falk, R. (1992). に書かれている "no-news, no-change" belief という説

Fox, C.R. & Levav, J. (2004). が提唱している Partition-edit-count モデルの Editing フェーズが省略されたケースだとする説

上記の仮説の評価　（筆者なりの）

 

特定事象による条件付確率あるいは事後確率の問題設定 のメンタルモデル

このメンタルモデルは、モンティホール問題に初めて触れた人が思いつくには複雑すぎると思う。条件付き確率の計算方法の知識があって、かつ、モンティ・ホール問題を条件付確率の問題として解くように指示されない限り無理だろう。
補足：
Tubau, E. & Alonson, D. (2003). が実験に使った対戦型モンティ・ホール問題では裏側から区別できないトランプカードを使っているので、もともと 特定事象による条件付確率あるいは事後確率の問題設定 になじまないかというと、そうでもない。 表から見れば、トランプカードはすべて異なるからである。 

不特定事象による条件付確率あるいは事後確率の問題設定  のメンタルモデル

このメンタルモデルであれば、対戦型にすることによって作られやすくなる理由がある。
    対戦型　→ カード 2枚の側の立場で考える　→　上で述べたメンタルモデル 

非条件付確率の問題設定 のメンタルモデル

このメンタルモデルでは、対戦型にしたところで、容易に作られるものではなさそうだ。 

確率継承説 のメンタルモデル

不特定事象による条件付確率あるいは事後確率の問題設定  のメンタルモデルと同様に、対戦型にすることによって作られやすくなりそうである。 

"Irrelevant, therefore invariant theorem" ヒューリスティク

Shimojo,S.,& Ichikawa,S.(1989). の "Irrelevant, therefore invariant theorem" 説や、 Falk, R. (1992). の "no-news, no-change" belief 説のような認知メカニズムが対戦型にすると起動されやすくなって、 その結果 Fox, C.R. & Levav, J. (2004). の Partition-edit-count モデルの Editing フェーズが省略されやすくなるのかも知れない。 

これらの評価の結果 (筆者なりの)

結論として、上で述べた 不特定事象による条件付確率あるいは事後確率の問題設定  のメンタルモデル、 もしくは 確率継承説 のメンタルモデル、 もしくは "Irrelevant, therefore invariant theorem" ヒューリスティクが 有望であるが、残念ながら現状では単なる私の想像でしかない。

参考文献

• De Neys, W. & Vershueren, N. (2006).
  Working memory capacity and a notorious brain teaser, Experimental Psychology, 53, 123-131.
  
• Falk, R. (1992).
  A closer look at the probabilities of the notorious three　prisoners.
  Cognition, 43, 197–223.
  
• Fox, C.R. & Levav, J. (2004).
  Partition-edit-count: Naive extensional reasoning in judgment of conditional probability,
  Journal of Experimental Psychology: General, 133, 626-642.
  
• Johnson-Laird, P. N., Legrenzi, P., Girotto, V., Legrenzi, M. S., & Caverni, J.-P. (1999).
  Naive probability: A mental model theory of extensional reasoning. Psychological Review, 106, 62-88.
  
• Shimojo,S.,& Ichikawa,S.(1989).
  Intuitive reasoning about probability:
  theoretical and experimental analyses of the "problem of three prisoners".
  Cognition, 32,1-24.
  
• Tubau, E. & Alonson, D. (2003).
  Overcoming illusory inferences in a probabilistic counterintu-iteive problem:
  The role of explicit representaitions. Memory & Cognition, 31, 596-607.
  

用語解説

• 特定事象による条件付確率あるいは事後確率の問題設定
  ホストが「これこれ」のハズレ扉を開けたということを証拠事象として、
  「それぞれ」の扉が当たりである条件付き確率を計算する問題設定である。
  標本空間を絞り込む範囲がホストが開けた扉に応じて変わる。
   
   
  
• 不特定事象による条件付確率あるいは事後確率の問題設定
  ホストが「いずれか」のハズレ扉を開けたかを証拠事象として、
  「挑戦者が選んだ」扉、あるいは「残りの」扉が当たりである条件付き確率を計算する問題設定である。
   
   
  
• 非条件付確率の問題設定
  ホストが「いずれか」のハズレ扉を開けることは最初から分っていることとして
  （相場用語なら「織り込み済み」だとして）
  「挑戦者が選んだ」扉、あるいは「残りの」扉が当たりである確率を計算する問題設定である。
  証拠事象によって標本空間の絞込みを行わない点が、「不特定事象による条件付確率あるいは事後確率の問題設定」との大きな違いである。
   
   
  
• 確率継承説
  挑戦者が選ばなかった二つの扉のどちらかが当りである確率は 2 / 3 なので、ホストがどちらかを開けて
  残った扉が、その 2 / 3 を引き継ぐという考え方である。 事象の独立性の概念を使っていないので、
  数学の確率論に立った考え方ではない。
   
   
  

トップページに戻る

---