トップページに戻る

封筒を開ける前に交換型の二封筒問題独自の錯覚現象

「封筒を開ける前に交換型」のニ封筒問題独自の錯覚現象について、モンティ・ホール問題で発生する錯覚と似ている点などを論じます。

無限増加の錯覚現象

「封筒を開ける前に交換型」の二封筒問題と「封筒と開けてから交換型」の二封筒問題で共通して、封筒を交換した後の金額の期待値が現在の金額の 1.25 倍だと錯覚します。
この錯覚に引きずられて、切り替えを繰り返すと、1.25 × 1.25 × 1.25 × ・・・・　のように無限に期待賞金額が膨らんでいくように思える点が、封筒を開ける前に交換型の二封筒問題独自の錯覚現象です。

これは、封筒を切り替えた後の金額の平均を出発点として次の切り替え後の金額の平均を計算できると勘違いしたことによります。

実際は、切り替え後の平均金額 1.25A を出発点として次の倍率予想をするためには、切り替え後の封筒に実際に入っている金額の A/2 と 2A のどちらの場合でも、次の切り替え後に平均金額が 1.25 倍になることを言わなければなりません。

しかし、平均金額の 1.25A でなく、封筒の中の具体的な金額 A/2 か 2Aを考えはじめたら、次のように期待賞金額が膨らんでいくことは有り得ないことに気が付きます。


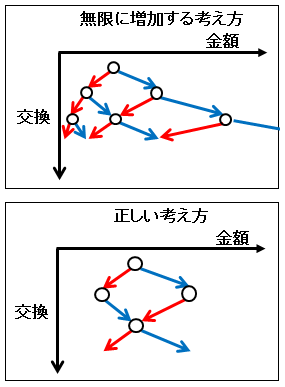
このことを図に画くと次のようになります。

この錯覚に関するモンティ・ホール問題との共通点

切り替える前の金額やその2倍や半分の金額を忘れて、平均金額だけで次のステップに進もうとする勘違いは、モンティ・ホール問題を考えるときに、挑戦者が選んだ扉が当たりかどうかが、ホストが開ける扉に関係することを忘れて、事後の標本空間を考えてしまう勘違いに似たところがあります。・・・ちょっとこじつけくさいですが・・・

パラドキシカル分布を考えたときの錯覚現象

この項を 2012/9/7 に一部書き直しました。
2014/01/16 に記述内容を一部簡素化しました。

「封筒を開けてから交換型」の二封筒問題の場合、金額の確率分布によっては常に封筒を交換した方が有利になることがあります。
二封筒問題のパラドキシカル分布参照

まったく同じ確率分布で 「封筒を開ける前に交換型」 の二封筒問題を考えたら、こちらの方も常に交換した方がよいのではないか、と心配になってきます。

この問題については パラドキシカル分布の謎 で調べてみました。



トップページに戻る

---