二つの封筒問題の錯覚とスマリヤンの錯覚の源は一つか

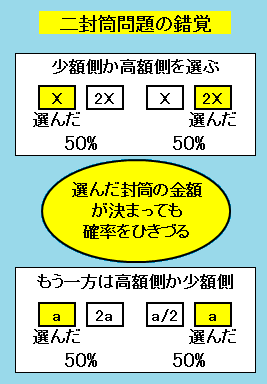
一見すると、二つの封筒問題の錯覚現象と、スマリヤンの錯覚は別の現象のように見えます。

二つの封筒問題では、二つの封筒の少額側や高額側の封筒を選ぶ確率と、選んだ封筒の金額 X について選ばなかった方の金額が 2X や X/2 である確率を混同する。
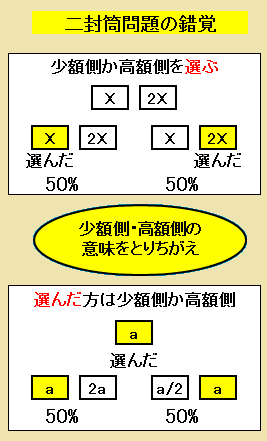
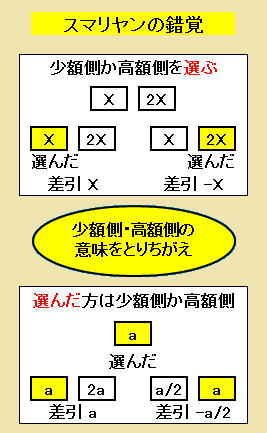
スマリヤンの錯覚では、二つの封筒の金額の組み合わせを、封筒のペアの金額に着目する見方と、選んだ封筒の金額に着目する見方を混同する。

しかし、これらの錯覚の構造を図解してみると、良く似ていることに気付きます。

それぞれの錯覚現象の構造

二つの封筒問題の錯覚現象とスマリヤンの錯覚構造の対比 1

二つの封筒問題の錯覚現象とスマリヤンの錯覚構造の対比 2

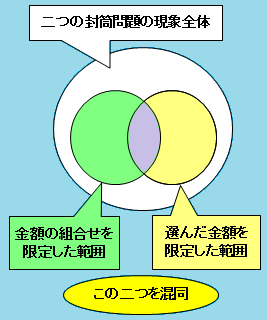
これらの錯覚現象は源を同じくしているか

上で見たように、二つの封筒問題の錯覚現象の構造と、スマリヤンの錯覚現象の構造がよく似ていることから、これら二つの錯覚現象がともに次のような同一の源から発しているのも知れません。

このような現象に、 Fox, C.R. & Levav, J. (2004). で提唱している "partition-edit-count" 説を応用すると、次のようになります。
いったん、金額の組み合わせで二つの封筒問題の現象に関する標本空間を分割 (partition) すると、選んだ封筒の金額という新しい要因を加味して標本空間を細分化することができないため、選んだ封筒の金額で行うべき標本空間の分割に、金額の組み合わせで行った標本空間の分割がそのまま転用されてしまうのだと思います。この最後の「転用」の部分が "partition-edit-count" 説の "edit" と同じような位置で働いています。

参考文献

Fox, C.R. & Levav, J. (2004).
Partition-edit-count: Naive extensional reasoning in judgment of conditional probability,
Journal of Experimental Psychology: General, 133, 626-642.

用語解説

スマリヤンの錯覚
私の造語です。
封筒を交換したらどうなるかを考えるときに、選んだ封筒の金額を条件として考えるやり方と、二つの封筒の金額の組み合わせを条件として考えるやり方が、同じ問題を考えているという錯覚です。
この錯覚に罹った人は、二封筒問題のおまじないの王様を唱えたり、スマリヤンの二つの文のパラドックスに罹ったりします。

トップページに戻る