トップページに戻る
変数誤用説を唱える人は、まったく別のパラドックスを感じているらしいという観点で、 2014/04/19 にこのページの内容や構成を大きく見直しましたが、その結果、ページが大きくなりすぎたので、整理を行いました。
2014/05/10
このおまじないを唱える人の心理に関する私の仮説を大きく二つに絞り込みました。
2014/06/10
このページの英語抜粋版 Inconsistent Variable Theory on The Two Envelope Paradox を作りました。
2014/08/31
「二つの封筒問題の原型問題にそぐわない」 という項を大幅に書き直しました。
2015/04/04
全体的に手を入れました。 内容を簡素化した段落や、全体を削除した段落、タイトルを替えた段落、削除した図があります。
選んだ封筒の金額から目をそむけ、二つの封筒の金額ペアの方に目を付けて納得しようとするおまじないは、ネットで高頻度で見かける他、パラドックスに関する通俗的な書籍でもこのおまじないを見かけます。 そして変数の使い方の誤りがパラドックスの原因だという主張と組み合さっているものを 「二封筒問題のおまじないの王様」 と呼ぶべきほど高頻度で見かけます。
そのように命名した後しばらくして、このおまじないを唱える人が二つの封筒問題を論じる人の中では1割にも満たなそうだと気づきました。
しかし、Wikipedia (英語版) の "Two envelopes problem" の記事でも、2005年から10年後の今日まで途切れることなくまともな議論の一つとして扱われ続けるなど、影響力を維持していそうなので、私はこのおまじないを唱える人の心理が気になってしようがありません。
このおまじないを唱えている論文を読むと、次のように論を展開するものが大部分です。
このような論文の例を以下にあげます。
変わり種として (1) の前に (2) を提示している論文を A. S. さんが 2007年 にネットで発表していますが、 (1) を考えるときにも (2) の考えを保持しなければならない理由を一言も述べていませんでした。
彼らが唱えるおまじないの文章に論理の飛躍があります。
½ × (x/2) + ½ × 2x
という式の左の x は交換して半減するときの値を表し、 · · · (1)
右の x は交換して倍増するときの値を表していて、 · · · (2)
同じ変数が別の値を表しているから、 · · · (3)
おかしくなるのである。
(1) と (2) から (3) は導けません。 (3) は単一の金額ペアを期待値の条件としたときに初めて導かれます。
しかし彼らは (1)、(2) から (3) が導かれて当然だと思っています。
別ページ 「変数誤用説の起源」 で調べたように 「単一金額ペアへの固執」 に捕らわれながらも 「変数の誤用説」 を唱えない人たちがいます。 例えば、二組の金額ペアを考えることがパラドックスの原因だと主張しながら変数の値が項によって異なることに言及しない人も 「変数の誤用説」 を唱える人に比べて少なくありません。 もしも 「変数の誤用説」 がデマでないとしたら、 「単一金額ペアへの固執」 に捕らわれたほぼすべての人が 「変数の誤用」 がパラドックスの原因であると気づきそうなものですから、疑問が起きます。
「変数の誤用」 が実際に人の頭の中で起きたとすると、次のようなプロセスだろうと思います。
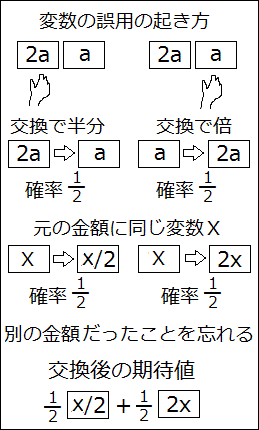
しかし、最後の 「別の金額だったことを忘れる」 というステップが人の頭で発生するとは、私には信じられません。
手持ちの金額を表す変数と確率変数をそれぞれ x, X とし、もう一方の金額を表す確率変数を Y とし、確率変数 R の条件付き期待値を E(R|条件) と表記することにして、比較してみます。
確率錯覚説では次のようになります。
変数の誤用説では次のようになります。
Wikipedia(英語版) の "Two envelopes problem" の記事 (01:06, 5 April 2014 の版) の "Common resolution" の "Mathematical details" の項に、選んだ封筒の金額も平均値で考えているものの 変数の誤用 によく似た説が書かれています。 (← 2014/12/21 に訂正)
これを真似て単一金額ペアでの 変数の誤用 を説明すると次のようになりました。
このように条件付き期待値の条件部分に確率変数 X が現れていて、 もともとの期待値計算式の形式からかけ離れてしまっています。 選んだ封筒の金額を変数や確率変数で表わしながら、単一の金額ペアに限定して議論することの難しさを示しています。
二つの封筒問題では、多くの場合、次のどちらかの文言があります。
(2) は Wikipedia(英語版) の "Two envelopes problem" の記事 (23:02, 29 April 2014. の版) の "Example" の項に書かれています。
私は、
しかし、 「変数の誤用説」 を唱える人は、
このような 「変数の誤用説」 の考え方は、 今手中にあるものを失うリスクを、 これから得るかも知れないものを得そこなうリスクより強く感じるという人間心理にそぐわないと思います。 そうした人間心理を踏まえれば、二つの封筒問題でも、今現在手にしている金額を中心にして考える傾向が強いだろうからです。 ← 2014/05/18 にこの文を加えました。
2015/04/05 にここにあった図を削除しました。
まずルールを説明します。
二つの封筒問題の普通の問題設定と、「変数の誤用説」 を唱える人にとっての問題設定を数式で表すと違いが引き立ちます。
記号の説明
選んだ封筒と他方の封筒の金額を表す確率変数をそれぞれ X、Y とし、
金額ペアを表す確率変数を P とします。
金額ペアに含まれる少額の方の金額で金額ペアを特定することができます。
このように、全く別の問題設定になっているにも関わらず、「変数の誤用説」 を唱える人が二つの封筒問題を解決したつもりになることに、 スマリヤンの錯覚 が関係していると思います。
私が 「単一金額ペアへの固執」 を起こしていて、なおかつ、金額に着目して考えたら、次のように考えるでしょう。
私が 「単一金額ペアへの固執」 を起こしていて、なおかつ、金額ペアに着目して考えたら、次のように考えるでしょう。
このように、「変数の誤用説」の大前提である金額ペアを一組に制限するという制約下では、パラドックスを感じること自体、困難です。
「変数の誤用」 が 「封筒を開ける前に交換型」 の二つの封筒問題のパラドックスの原因だとすると、「封筒を開ける前に交換型」 と 「封筒を開けてから交換型」 とで全く別の心理現象がパラドックスを起こすことになります。「封筒を開けてから交換型」 では 「変数の誤用」 が起こり得ないからです。 こんな器用なパラドックスを人間心理が起こすとは信じられません。
このおまじないは、
という、二封筒問題本来のパラドックスの答えになっていません。「本来」 のパラドックスを感じている人から見ると、このおまじないは、一組の金額ペアに視野を制限してパラドックスを見えなくしているだけ、 あるいは二つの封筒が互角であることを確認して振り出しに戻っただけに思えます。
パラドックスとは、ある考え方が導く矛盾のことなのだから、他の考え方が矛盾を導くかどうかは関係ありません。 あくまでも金額ペアではなく金額の方を中心に考えなければ、 あるいは期待値計算式の中の変数記号が式全体で同じ値を意味していると解釈しなければ、 二つの封筒問題の 「本来の」 パラドックスを解消したと主張することはできません。 (← 2014/05/11 に書き足しました)
変数を誤用するためには期待値計算式を明確にする必要がありますが、計算式を明記したら変数の誤用は起き難くなります。
計算式を明記しなくても倍率の平均や加減算の錯覚や損得勘定での変数の誤用なら起こり得るので、こちらの方が信憑性が高いと思います。
( · · · 計算式を明記したら倍率の平均や加減算の錯覚も損得勘定での変数の誤用も起き難くなりますが · · · )
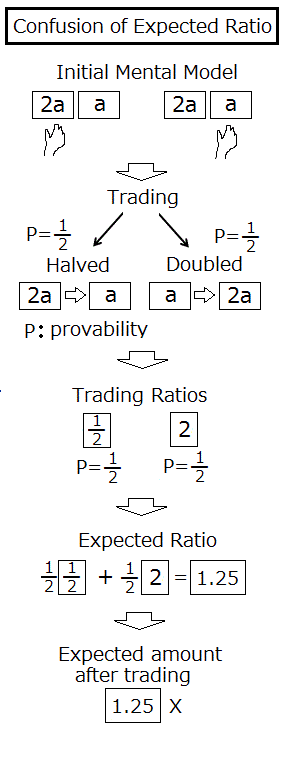
倍率の平均の錯覚
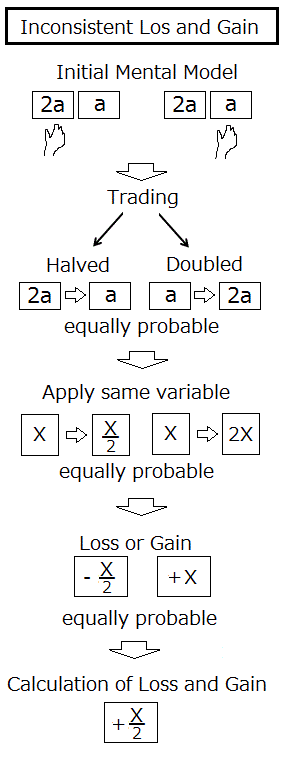
損得勘定での変数の誤用
二つの封筒問題の最初の原型問題 「ネクタイのパズル」 について Wikipedia (英語版) の "Necktie paradox" の記事 (16:27, 18 December 2013 の版) に書かれている問題文を調べると、次のような順序で書かれていました。
Martin Gardner が1981年の Aha! Gotcha に載せた 「財布のゲーム」 のパズルは、二つの封筒問題の原型の一つです。
Kent G. Merryfield, Ngo Viet, and Saleem Watson (1997). によると次のような問題だったそうです。
二人の男が相手の財布の中身を知らないことは明白ですが、自分の財布の中身を知っているかどうかは不明です。
「ネクタイのパズル」 や 「財布のゲーム」 を読んだ人は 「変数の誤用」 を起こしやすいかもしれません。
しかし、上記の 「ネクタイのパズル」 や 「財布のゲーム」 の問題文と 「二つの封筒問題」 の問題文との間には次のような違いがあるので、そうやすやすとは 「二つの封筒問題」 で 「変数の誤用」 が起こらないでしょう。
パラドックスの源として書かれている期待値計算式を見てから、そこに書かれているx/2, 2x という記号に合わせて 「変数の誤用」 を起こすことができるでしょうか?
2015/04/05 に内容を整理しました。
Nalebuff, Barry. (1988). に、 彼の元に二つの封筒問題が届くまでの経路が書かれていて、それ以上さかのぼることは出来ないとしています。
Barry Nakebuff ← H. V. さん ← S. Zabell ← S. B. さん
Nalebuff, Barry. (1988). に出てくる 「アリさんに封筒を渡してからババさんに渡す封筒の金額を決める型」 の問題文が 「封筒を開けてから交換型」 であることと、 Zabell, S.L. (2005). の中に書かれている二つの封筒問題が 「封筒を開けてから交換型」 であることから、 Nalebuff さんに伝わった二つの封筒問題を遡った果ての問題が同じように 「封筒を開けてから交換型」 だった可能性があります。 Zabell, S.L. (2005). は Nalebuff さんに二つの封筒問題が伝わった 1988 年ごろから 17年程後の出版なので、参考程度にしかなりませんが · · ·
Zabell, S.L. (2005). の中に書かれている二つの封筒問題は次のような展開になっています。
つまり、二つの封筒問題のパラドックスは、歴史的には、選んだ封筒の金額を含む二組の金額ペアを考慮したときのパラドックスとして出発したことになります。
Wikipedia(英語版)の "Two envelopes problem" の記事 (23:02, 29 April 2014 の版) によると、 1996年に数学者によって書かれた論文が 「変数の誤用説」 の先駆けだそうです。
つまり、歴史的には 「変数の誤用説」 は二つの封筒問題が世に出てから数年後に出て来た新参者ということになります。
スマリヤンが Smullyan, Raymond (1992). で 「スマリヤンの二つの文のパラドックス」 を編み出した時期の方が早そうなので、 「数学者」 スマリヤンが 「変数の誤用説」 を唱える 「哲学者」 たちをからかうために、「スマリヤンの二つの文」 を考えたという私の推測は間違いでしょう。 (← 2015/04/06 に表現を戻しました)
といった具合に、 自分自身の体験談として語っている論文を見たことがありません。 (← 2014/05/11 に詳しく書き直しました)
といった具合に、 心理学説として語っている人も見かけたことがありません。 (← 2014/04/26 に書き加えました)
「変数の誤用現象」 が実際に起きるものなら、次のような 「変数の誤用現象」 をさらに起きやすくする問題文が考案されそうなものです。
しかしこのような 「変数誤用説におあつらえ向き」 の問題文を見たことがありません。
Zabell, S.L. (2005). の中に書かれている二つの封筒問題は次のような展開になっていて、「変数誤用説に 多少 おあつらえ向き」 な箇所もあります。
2014/09/28 にこの箇所を書き足しました。
Wikipedia(英語版)の "Two envelopes problem" の記事 (23:02, 29 April 2014. の版) の冒頭部分は次のようになっています。
上記の (1) と (2) が矛盾していることに気付いたのは私だけでしょうか?
Wikipedia(英語版)の "Two envelopes problem" の記事 (21:39, 23 November 2014 の版) の "Simple resolutions " の項に書かれている説の一つは、 選んだ封筒の金額も平均値で考えているものの 「変数の誤用説」 によく似ているので、それをザックリまとめると次のようになります。
この事実は全く予想外で衝撃的だったため、このおまじないがデマだと自信を持って言えなくなりました。
長い間ネットで調べても彼の論文を読むことができなかったのですが、2015年になってやっと読むことができました。2015年の4月1日にこの論文のコピーをやっと手にいれることができました。 → 「変数の誤用説」 を唱えた数学者は二つの封筒問題を勘違いしていた?
彼も 「確率の錯覚」 を起こしていたであろう痕跡を論文の中に見つけることはできませんでしたが、 彼が自分の体験として語っている箇所も見当たりませんでした。
特筆すべきことは二組の金額ペアを考えることが原因で誤った期待値計算式が出来上がったと主張していることです。 (← 2015/09/23 訂正)
「変数の誤用」 の方は期待値計算式の誤りを説明するために副次的に取り上げられていました。
「変数の誤用説」を唱える多くの論文にこの論文が 「変数の誤用説」 の元祖として引用されているのは、誤解に基づいていたのです。
そんな論文を読んでしまったために、二つの封筒問題のパラドックスは確率の錯覚が原因だという説に対する自信が揺らいでしまいました。 「変数の誤用」 という心理現象を起こす人たちも実際に存在していて、この論文を書いた心理学者本人もその一人かも知れないと思ったのです。
その論文の内容
この心理学者は自分の仕事を忘れたらしい
彼女は二組の金額ペアを考えること自体がパラドックスの原因だと思い込んでしまったので、確率の錯覚現象の方にまったく目が行かなくなったのでしょう。
2015/04/05 内容を一部修正しタイトルも変えました。
このおまじないは次の二つの主張に分解することができます。
(2) の方は、(1) を説明するための補足ではなくて二つの封筒が互角であることを確認したい気持ちの表れ、すなわち 「おまじない」 ではなくて、 (1) がデマでないことを示すためにわざわざ (2) を示しているのかも知れません。
このおまじないは上で見たように非常に奇妙ですが、 残念ながら現状では次のような理由から間違いを論証できません。
このおまじないを、ネット上記事で読んだり、論文で読んだりしているうちに、このおまじないを唱える人の共通点が浮かび上がってきました。
ある論文では、封筒が二つしかないから金額も二つしかないと述べていました。
もう一つの論文では、冒頭から二つの金額だけを変数で明記して議論を初めていました。
まだ私が知っている事例が少ないのですが、無視できません。 ← 2014/05/18 にこの文を加えました。
上記をふまえて、このおまじない (変数誤用説) を唱える人の心理プロセスについて仮説を考えてみました。
2015/04/05 に全体的に以下の記述を簡素化しました。
このおまじないを唱える人は 「単一金額ペアへの固執」 が強いのかも知れません。
そうなる理由としては、封筒のどちらかを選ぶ前の封筒の中身のイメージ、すなわち 「神の視点」 から逃れられないためかも知れません。
そして、封筒が二つだから金額の数も二つでなければならないという理論を思いついて、 数学が得意な人なら思いもよらない別種のパラドックスに行き着いたのかも知れません。
彼らが単一の金額ペアのイメージに合わせて期待値の計算式を解釈するためには、彼らに次のような条件が必要でしょう。
「確率の錯覚」 が特に強烈なため、期待値計算式の確率部分には全く目が行かなくて、苦し紛れに、変数の方に目を付けたのでしょう
彼らが 「確率の錯覚」 を忘れてしまうためには、彼らに次のような条件が必要でしょう。
仮説 2 【自己欺瞞説】で述べたような特性の人たちが 「変数の誤用説」 を読むと納得して暗示に掛かってしまうのかも知れません。 そして自分たちが変数の誤用を起こしていたと思い込んだのかも知れません。
一度は期待値計算式を理解してパラドックスの存在を理解した人が、金額 A と 2A だけで期待値計算式を組み立てるとパラドックスが回避できることに気づいたために、金額 x/2 と 2x で期待値計算式を考えること、つまり二組の金額ペアを考えることがパラドックスの原因だと勘違いしたのかも知れません。
そして、一度は二組の金額ペアを考えていたこととの矛盾を解消するために、自分たちが変数の誤用を起こしていたと思い込もうとしているのかも知れません。
彼らは数学が苦手で、特に変数に慣れておらず、期待値の概念もよく理解していないために混乱を来したのかもしれません。そして数学が得意な人なら思いもよらない別種のパラドックスに行き着いたのかも知れません。
彼らが読んだ問題文に、選んだ封筒の金額と他方の封筒の金額を変数記号で表した式があって、それが 「方程式」 あるいは 「関係式」 に見えるような書き方だったのかも知れません。そして通常の問題文なら思いもよらない別種のパラドックスに行き着いたのかも知れません。確率 1/2 でA/2 であり、確率 1/2 で2A である」 と書かれていた場合と、上記の (1) のように書かれていた場合とで、変数記号の解釈が変わってくるのかも知れません。
Wikipedia(英語版)の "Two envelopes problem" の記事(21:39, 23 November 2014 の版)の "Introduction to further developments in connection with Bayesian probability theory" の項に書かれていた記述をヒントに、この仮説を思いつきました。仮説 5 【
2015/08/29 にこの項を加えました。
彼らは期待値計算式の意味をよく理解していないために、E = (1/2)(x/2) + (1/2)2x が E = (1/2)a + (1/2)2a の書き間違いだと勘違いしたのかも知れません。
実験で用いる問題文は次のような観点で変化をつけるとよいと思います。
被験者を一旦、 「変数の誤用説」 に誘導しておいてから、その説では「封筒を開けてから交換型」の問題を解決できないことを示したときの被験者の反応も調べていただきたいと思います。 ← 2014/05/06 にこの文を追加しました。
被験者に 「交換して倍になったときと半分になったときの金額の比はどのくらいか」 という、スマリヤン的な質問をぶつけるのも良いと思います。
4 対 1 という回答が大勢を占めたら、 「変数の誤用説」 は常識的には誤り ということになりますが、2 対 1 という 「変数の誤用説」 に有利な回答が少なくないかも知れません。
← 2014/05/06 にこの文を追加しました。
このおまじないを唱える人自身が確率の錯覚をしていたことが心理学実験で証明されれば、このおまじないは誤りであると結論できるでしょう。
「封筒を開ける前に交換型」 の二つの封筒問題でも、期待値計算式の中の記号が特定の値を表していると解釈する人の方が多いことが、心理学実験で証明されれば、このおまじないは 「常識的には」 誤りであると結論できるでしょう。 ← 2014/04/16 にこの文を書き換えました。
「変数の誤用説」 を唱える人たちの心理を心理学者が実験で解明するまで、はっきりしたことを言えませんが、上記の私の仮説の中では次の仮説を最も有望視しています。
この仮説が正しければ、この「二封筒問題のおまじないの王様」 は、それをを唱える本人を含めてだれも感じたことのない実在しない架空のパラドックスを解決しているのです。
E(E(B|A) - A) (選んだ封筒の金額を条件とする期待交換利得)や
E(B - E(A|B)) (選ばなかった方の封筒の金額を条件とする期待交換利得)と異なり、
E(E(B - A|A+B)) (二つの封筒の金額の和を条件とする交換利得の平均でゼロに等しい) だけが、数列の部分和の組み立てに対称性を respect している。
この論文 (Clark, Michael. & Shackel, Nicholas. (2000).) では、一方の封筒の金額を条件とした期待利得を考えることには正当性を認めず、両方の封筒の金額ペアを条件とした期待利得を考えることだけに正当性を認めているようです。そして、「対称性」 や 「ゼロに等しい」 という理由以上の根拠が書かれていないようなので、この有名な論文も、私には 「二封筒問題のおまじないの王様」 に見えます。
余談
私が 二封筒問題のパラドックスたち で述べた 「神様視点のパラドックス」 に執筆者が罹っていることを思わせる記述もこの論文の中にあります。
Wikipedia(英語版) の "Two envelopes problem" の記事 (23:02, 29 April 2014 の版) に 「変数の誤用説」 の先駆けだと書かれている論文 (1996年) の執筆者が 「哲学者」 ではなくて 「数学者」 であることに 2014/05/04 に気付いて以来、関心を持っていました。
2015/04/01 にその論文のコピーを得ることができたので、さっそく読んでみました。 その内容を一言で言うと次のようになります。
【内容の1】主たる主張
【内容の2】主たる主張の解説
【内容の3】reference point という独特の用語
2015/09/23 にこの項を加えました。
この論文では "reference point" という独特の用語が2か所で使われています。お金を封筒に入れる段階では最初の金額Sに対して次の金額がS/2でも2Sでもあり得ることを "reference point" という用語が示していると私は誤解して「視点の誤り」だの「着目した時点の誤り」だのと訳しましたが、どうやら間違いのようです。
次のような言い回しがあるので、同じ記号Sが変数の意味と確率変数の意味の両方を持っていることを指しているようにも思えますが、よくわかりません。
この数学者は 「変数の誤用説」 を唱えていなかった。
上記の「主たる主張の解説」 の部分だけ読むと、この論文の著者が 「変数の誤用説」 を唱えているように思う人が多いでしょう。
しかしこの著者自身は「変数の誤用」がパラドックスの直接の原因だと思っていないことが、論文を読んでわかりました。
「二組の金額ペア」 によってできあがった期待値計算式に 「単一の金額ペア」 を当てはめて解釈すると 「変数の誤用」 が見いだせるのであって、「変数の誤用」 が間違った期待値計算式を作ったわけではなかったのです。
この数学者の勘違い
2015/9/5 にやっと、この数学者がどんな勘違いしたかひらめきました。
Wikipdia(英語版)のデマ
Wikipedia(英語版) の "Two envelopes problem" の記事 (23:02, 29 April 2014 の版) の "Common resolution" の項に書かれている次の文は 「デマ」 なのだと、私は思っています。
トップページに戻る
2018/03/06 22:43:05
大改訂 2014/04/19, 2014/04/26
初版 2013/11/30
二封筒問題のおまじないの王様 – 変数誤用説 –
2014/04/26変数誤用説を唱える人は、まったく別のパラドックスを感じているらしいという観点で、 2014/04/19 にこのページの内容や構成を大きく見直しましたが、その結果、ページが大きくなりすぎたので、整理を行いました。
2014/05/10
このおまじないを唱える人の心理に関する私の仮説を大きく二つに絞り込みました。
2014/06/10
このページの英語抜粋版 Inconsistent Variable Theory on The Two Envelope Paradox を作りました。
2014/08/31
「二つの封筒問題の原型問題にそぐわない」 という項を大幅に書き直しました。
2015/04/04
全体的に手を入れました。 内容を簡素化した段落や、全体を削除した段落、タイトルを替えた段落、削除した図があります。
選んだ封筒の金額から目をそむけ、二つの封筒の金額ペアの方に目を付けて納得しようとするおまじないは、ネットで高頻度で見かける他、パラドックスに関する通俗的な書籍でもこのおまじないを見かけます。 そして変数の使い方の誤りがパラドックスの原因だという主張と組み合さっているものを 「二封筒問題のおまじないの王様」 と呼ぶべきほど高頻度で見かけます。
そのように命名した後しばらくして、このおまじないを唱える人が二つの封筒問題を論じる人の中では1割にも満たなそうだと気づきました。
しかし、Wikipedia (英語版) の "Two envelopes problem" の記事でも、2005年から10年後の今日まで途切れることなくまともな議論の一つとして扱われ続けるなど、影響力を維持していそうなので、私はこのおまじないを唱える人の心理が気になってしようがありません。
二封筒問題のおまじないの王様の構造
このおまじないは次のような構成になっています。|
選んだ方の封筒の金額を x とする。
もう一つの封筒の金額 Y の期待値は ということは常に封筒を交換した方がよいことになる。 おかしい。 |
| ↓ |
|
このようなおかしな結果になるのは、
という式の左の x は交換して半減するときの値を表し、 右の x は交換して倍増するときの値を表していて、 同じ変数が別の値を表しているから、おかしくなるのである。 次のようにすればよい。 二つの封筒の金額ペアを (a, 2a) とし、 選んだ封筒ともう一方の封筒の金額の確率変数をそれぞれ X, Y とすると、 こうしてパラドックスを避けることができた。 |
このおまじないの奇妙な点
論理的に奇妙である
2014/11/24 にこの項を加えました。このおまじないを唱える人は単一の金額ペアで考える必然性を述べていない
2014/05/24 にこの項を作り、2014/11/24 に位置を変更しました。このおまじないを唱えている論文を読むと、次のように論を展開するものが大部分です。
- x/2 と 2x を含む期待値計算式を提示 – – – (1)
- 金額ペアが一つ (例: A と 2A のペア) であることを強調する – – – (2)
- x/2 と 2x を含む期待値計算式と、A と 2A のペアが合わないことを指摘する
このような論文の例を以下にあげます。
- F. T. B さんが 1996年にある論文誌に発表した論文 (Wikipedia(英語版) の "Two envelopes problem" の記事でこういった説の先駆けとして紹介)
- R. F. さんが 2008年にある論文誌に発表した論文
- F. O. さんが 2010年にネットで発表した論文
変わり種として (1) の前に (2) を提示している論文を A. S. さんが 2007年 にネットで発表していますが、 (1) を考えるときにも (2) の考えを保持しなければならない理由を一言も述べていませんでした。
単一の金額ペアを考えるところから 「変数の誤用説」 にまで進んだ人たちは、論理の飛躍に気付いていない
2014/05/06 にこの項を加え、2014/11/24 に位置と表題を変えました。彼らが唱えるおまじないの文章に論理の飛躍があります。
という式の左の x は交換して半減するときの値を表し、 · · · (1)
右の x は交換して倍増するときの値を表していて、 · · · (2)
同じ変数が別の値を表しているから、 · · · (3)
おかしくなるのである。
(1) と (2) から (3) は導けません。 (3) は単一の金額ペアを期待値の条件としたときに初めて導かれます。
しかし彼らは (1)、(2) から (3) が導かれて当然だと思っています。
心理学的にも奇妙である
「単一金額ペアへの固執」 に捕らわれながらも 「変数の誤用」 がパラドックスの原因であると気づかない人がいる
2014/11/24 にこの項を加え、2015/04/05 にタイトルを変えました。別ページ 「変数誤用説の起源」 で調べたように 「単一金額ペアへの固執」 に捕らわれながらも 「変数の誤用説」 を唱えない人たちがいます。 例えば、二組の金額ペアを考えることがパラドックスの原因だと主張しながら変数の値が項によって異なることに言及しない人も 「変数の誤用説」 を唱える人に比べて少なくありません。 もしも 「変数の誤用説」 がデマでないとしたら、 「単一金額ペアへの固執」 に捕らわれたほぼすべての人が 「変数の誤用」 がパラドックスの原因であると気づきそうなものですから、疑問が起きます。
「変数の誤用」 が実際に人の頭の中で起きる様子を想像しづらい
2014/11/24 にこの項の位置を変えました。「変数の誤用」 が実際に人の頭の中で起きたとすると、次のようなプロセスだろうと思います。
しかし、最後の 「別の金額だったことを忘れる」 というステップが人の頭で発生するとは、私には信じられません。
心理学的に複雑すぎる
封筒を交換した方がよいかどうか、選んだ封筒の金額を思考の中心に置いて考えようとしている人の心理を考えてみます。 そうしながら 「変数の誤用」 と 「確率の錯覚」 を比較すると、「変数の誤用」 の方がはるかに心理学的に複雑な現象であることがわかります。手持ちの金額を表す変数と確率変数をそれぞれ x, X とし、もう一方の金額を表す確率変数を Y とし、確率変数 R の条件付き期待値を E(R|条件) と表記することにして、比較してみます。
確率錯覚説では次のようになります。
g(z) を (z, 2z) という金額ペアが成立する確率とすると、 ← 2014/05/10 に書き直しました。
E(Y|X=x)
= (g(x/2) / (g(x/2)+g(x))) (x/2) + (g(x) / (g(x/2)+g(x))) 2x
= ½ (x/2) + ½ 2x
g(x/2) / (g(x/2)+g(x)) や g(x) / (g(x/2)+g(x)) は不明であるにもかかわらず、どちらも 1/2 だと錯覚することがパラドックスの原因である
変数の誤用説では次のようになります。
Wikipedia(英語版) の "Two envelopes problem" の記事 (01:06, 5 April 2014 の版) の "Common resolution" の "Mathematical details" の項に、選んだ封筒の金額も平均値で考えているものの 変数の誤用 によく似た説が書かれています。 (← 2014/12/21 に訂正)
これを真似て単一金額ペアでの 変数の誤用 を説明すると次のようになりました。
選んだ封筒ともう一方の封筒の金額を表す確率変数をそれぞれ、 X、Y とし、
金額ペアを表す確率変数を P とすると、
E(Y | P=(a, 2a))
= E(Y | X = 2a かつ P=(a,2a) ) + E(Y | X = a かつ P=(a,2a))
= P(X = 2a | P=(a,2a)) × a + P(X = a | P=(a,2a)) × 2a
= ½ × a + ½ × 2a · · · (1)
確率変数 X から変数 a や 2a へ切り替えるべきところを切り替わらず、(1) が½ (X/2) + ½ 2X になってしまったことがパラドックスの原因である。
(この欄を 2014/12/14 に訂正)
確率変数 X から変数 a や 2a へ切り替えるべきところを切り替わらず、(1) が
(この欄を 2014/12/14 に訂正)
このように条件付き期待値の条件部分に確率変数 X が現れていて、 もともとの期待値計算式の形式からかけ離れてしまっています。 選んだ封筒の金額を変数や確率変数で表わしながら、単一の金額ペアに限定して議論することの難しさを示しています。
人間心理として奇妙である
2014/05/06 にこの項を加えました。二つの封筒問題では、多くの場合、次のどちらかの文言があります。
- 選んだ封筒の金額を x とすると · · ·(1)
- 選んだ封筒の金額が例えば幾ら幾らだとすると · · ·(2)
(2) は Wikipedia(英語版) の "Two envelopes problem" の記事 (23:02, 29 April 2014. の版) の "Example" の項に書かれています。
私は、
(1) であれ (2) であれ、このような問題を出された人は、 封筒を交換して今現在手にしている金額の倍になるか、半分になるかと悩むものだ。
と思います。
← 2014/05/18 に枠内を書き換えました。2015/04/06 にも少し書き足しました。
しかし、 「変数の誤用説」 を唱える人は、
このような問題を出された人は、 今現在手にしている封筒は交換したら倍になる方の封筒か半分になる方の封筒かと悩みながら、 期待値を計算するときにだけ間違えたのだ。
と思っているかのようです。
← 2014/05/18 に枠内を書き換えました。
このような 「変数の誤用説」 の考え方は、 今手中にあるものを失うリスクを、 これから得るかも知れないものを得そこなうリスクより強く感じるという人間心理にそぐわないと思います。 そうした人間心理を踏まえれば、二つの封筒問題でも、今現在手にしている金額を中心にして考える傾向が強いだろうからです。 ← 2014/05/18 にこの文を加えました。
数学的に奇妙である
- 金額ペアを a と 2a の組み合わせに限定して、しかも手持ちと他方の金額の期待値を比較する問題にしたらパラドックスが発生する余地がなくなってしまいます。 それらが等しいことを述べるのにいちいち計算式を立てる必要すらありません。
- 「封筒を開けてから交換型」 の場合に意味をなしません。
- そもそも、変数の使い方を間違えることは、色々な生徒を教えている数学の先生でもないかぎり、数学の得意な人には想像もつきません。 (実際、論文等でこのおまじないを唱えている数学者は私が調べた範囲で一人しかいませんでした)
- 二つの封筒問題の原型問題 「ネクタイのパラドックス」 を発表した人が数学者であったことと矛盾します。 彼自身が変数の使い方を誤っていたとしたら、彼の行為は自分自身の恥をさらすことになるからです。 ← 2014/06/07 に追記
← 2015/02/08 に訂正 ( 二つの封筒問題を世に広めた数学者 Nalebuff, Barry. (1988). は 「開けてから交換型」 の二つの封筒問題を論じているので、 「変数の誤用」 とは無縁でした)
問題のすり替えに見える
このおまじないは選んだ封筒の金額を条件とする、もう一方の封筒の金額の条件付き期待値の問題から、 単一の金額ペアの配置の問題にすり替えているように見えます。2015/04/05 にここにあった図を削除しました。
単一の金額ペアで考える人は 「神の視点」 で確率を考えているように見える
E. M. さんの"The Two Envelope Problem" というページの記述は次のような展開でした。まずルールを説明します。
- 1つの封筒に $X を入れ、他方に $2X を入れる。
- あなたは封筒を選んで中身を見る。
- 見た後で交換してもよい。
- 「封筒を開けてから交換型」 であるにも関わらず、選んだ封筒の金額を確率変数とします。
- それでいながら、封筒の金額を $X と $2X に固定します。
- 変数の意味をすり替えるというよりは、条件付き確率の条件の方をすり替えています。 (条件の中に、二つの金額しか登場しないようにしています)
数式で表すと、全く別の問題を考えていることがわかる
2014/05/06 にこの項を加えました。二つの封筒問題の普通の問題設定と、「変数の誤用説」 を唱える人にとっての問題設定を数式で表すと違いが引き立ちます。
記号の説明
選んだ封筒と他方の封筒の金額を表す確率変数をそれぞれ X、Y とし、
金額ペアを表す確率変数を P とします。
金額ペアに含まれる少額の方の金額で金額ペアを特定することができます。
| 普通の問題設定 |
「変数の誤用説」 の 問題設定 |
|
|---|---|---|
|
期待値の 条件 |
選んだ封筒の金額 | 金額ペア |
|
考慮する 金額ペア |
選んだ封筒の金額 x を含む 二組の金額ペア |
期待値の条件とする 金額ペアのみ |
|
開ける前に 交換型 での 比較対象 |
|
|
|
開けた後に 交換型 での 比較対象 |
↓ すべての x を考えると ↓ |
対応不可能 |
| パラドックス |
∴ E(Y) > E(X) |
no paradox |
|
保持する 条件 |
期待値計算式に x/2 の項と 2x の項を 持つこと |
期待値計算式の 各項の確率係数が 1/2 であること |
このように、全く別の問題設定になっているにも関わらず、「変数の誤用説」 を唱える人が二つの封筒問題を解決したつもりになることに、 スマリヤンの錯覚 が関係していると思います。
私が 「単一金額ペアへの固執」 を起こしていても 「変数の誤用説」 が想定する心理現象は起こさない
2014/05/05 にこの項を加えました。私が 「単一金額ペアへの固執」 を起こしていて、なおかつ、金額に着目して考えたら、次のように考えるでしょう。
こっちの封筒の金額を x と置いたときの、もう一方の封筒の金額の期待値は
P(あっちが少額 | こっちがx)(x/2) + P(こっちが少額 | こっちがx)(2x)
だから、 金額ペアを (A, 2A) と置くと、
x = A なら
P(あっちが少額 | こっちがx)(x/2) + P(こっちが少額 | こっちがx)(2x) = 0×(A/2) + 1×2A = 2A 。
x = 2A なら
P(あっちが少額 | こっちがx)(x/2) + P(こっちが少額 | こっちがx)(2x) = 1×(2A/2) + 0×A = A 。
要するに、こっちが A ならあっちは 2A、 こっちが 2A ならあっちは A 。
これのどこがパラドックスなのだろう???
だから、 金額ペアを (A, 2A) と置くと、
x = A なら
x = 2A なら
要するに、こっちが A ならあっちは 2A、 こっちが 2A ならあっちは A 。
これのどこがパラドックスなのだろう???
私が 「単一金額ペアへの固執」 を起こしていて、なおかつ、金額ペアに着目して考えたら、次のように考えるでしょう。
金額ペアを (A, 2A) と置いたときの、こっちの封筒の金額の期待値は
P(こっちが少額)2A + P(あっちが少額)A = その金額ペアの金額の平均 。
あっちの封筒の金額の期待値は
P(こっちが少額)A + P(あっちが少額)2A = その金額ペアの金額の平均 。
これのどこがパラドックスなのだろう???
あっちの封筒の金額の期待値は
これのどこがパラドックスなのだろう???
このように、「変数の誤用説」の大前提である金額ペアを一組に制限するという制約下では、パラドックスを感じること自体、困難です。
「封筒を開ける前に交換型」 と 「封筒を開けてから交換型」 とで別の心理現象が起きるとは信じられない
2014/04/28 にこの項を加えました。「変数の誤用」 が 「封筒を開ける前に交換型」 の二つの封筒問題のパラドックスの原因だとすると、「封筒を開ける前に交換型」 と 「封筒を開けてから交換型」 とで全く別の心理現象がパラドックスを起こすことになります。「封筒を開けてから交換型」 では 「変数の誤用」 が起こり得ないからです。 こんな器用なパラドックスを人間心理が起こすとは信じられません。
このおまじないを唱えない人から見て、パラドックスの解明になっていない
2014/04/26 にこの項を加えました。このおまじないは、
「選んだ封筒の金額を条件とする、封筒を交換したときの利得の期待値 (注1, 注2) が金額によらず正だとしたら、封筒を開けなければどちらの封筒も互角であるのはなぜか」
という、二封筒問題本来のパラドックスの答えになっていません。「本来」 のパラドックスを感じている人から見ると、このおまじないは、一組の金額ペアに視野を制限してパラドックスを見えなくしているだけ、 あるいは二つの封筒が互角であることを確認して振り出しに戻っただけに思えます。
パラドックスとは、ある考え方が導く矛盾のことなのだから、他の考え方が矛盾を導くかどうかは関係ありません。 あくまでも金額ペアではなく金額の方を中心に考えなければ、 あるいは期待値計算式の中の変数記号が式全体で同じ値を意味していると解釈しなければ、 二つの封筒問題の 「本来の」 パラドックスを解消したと主張することはできません。 (← 2014/05/11 に書き足しました)
- 注1:
利得 = 交換した後の金額 - 交換する前の金額 - 注2:
利得の期待値 = 交換した後の金額の期待値 - 交換する前の金額
「変数の誤用説」 よりも 「倍率の平均や加減算の錯覚説」 や 「損得勘定での変数の誤用説」 の方が信憑性が高い
2014/04/20 にこの項を加えました。変数を誤用するためには期待値計算式を明確にする必要がありますが、計算式を明記したら変数の誤用は起き難くなります。
計算式を明記しなくても倍率の平均や加減算の錯覚や損得勘定での変数の誤用なら起こり得るので、こちらの方が信憑性が高いと思います。
( · · · 計算式を明記したら倍率の平均や加減算の錯覚も損得勘定での変数の誤用も起き難くなりますが · · · )
倍率の平均の錯覚
損得勘定での変数の誤用
二つの封筒問題の原型問題にそぐわない
2014/08/31 にこの項を大幅に書き直しました。二つの封筒問題の最初の原型問題 「ネクタイのパズル」 について Wikipedia (英語版) の "Necktie paradox" の記事 (16:27, 18 December 2013 の版) に書かれている問題文を調べると、次のような順序で書かれていました。
二人の男のそれぞれが、妻たちからクリスマスにプレゼントされたネクタイを締めている。
ネクタイの値段を妻たちから聞いて、値段の高い方の男がそのネクタイを相手に譲るという賭けをする。
以下は一人の男の頭の中の記述
自分のネクタイが少額側である確率も高額である確率も 1/2 だ。
自分のネクタイが高額側なら自分のネクタイの値段に等しい損をする。
自分のネクタイが少額側なら自分のネクタイの値段を上回る得をする。
自分の方が有利だ。
ネクタイの値段を妻たちから聞いて、値段の高い方の男がそのネクタイを相手に譲るという賭けをする。
以下は一人の男の頭の中の記述
自分のネクタイが少額側である確率も高額である確率も 1/2 だ。
自分のネクタイが高額側なら自分のネクタイの値段に等しい損をする。
自分のネクタイが少額側なら自分のネクタイの値段を上回る得をする。
自分の方が有利だ。
Martin Gardner が1981年の Aha! Gotcha に載せた 「財布のゲーム」 のパズルは、二つの封筒問題の原型の一つです。
Kent G. Merryfield, Ngo Viet, and Saleem Watson (1997). によると次のような問題だったそうです。
二人の男がそれぞれの財布をテーブルに置く。
自分の財布に最少額の金額が入っていたら相手の財布の金を勝ち取る。
お互いが次のように考えた。
自分は手持ちの金額を失うかもしれないが、それ以上を得るかもしれない。
だからこのゲームは自分に有利だ。
自分の財布に最少額の金額が入っていたら相手の財布の金を勝ち取る。
お互いが次のように考えた。
自分は手持ちの金額を失うかもしれないが、それ以上を得るかもしれない。
だからこのゲームは自分に有利だ。
二人の男が相手の財布の中身を知らないことは明白ですが、自分の財布の中身を知っているかどうかは不明です。
「ネクタイのパズル」 や 「財布のゲーム」 を読んだ人は 「変数の誤用」 を起こしやすいかもしれません。
- 「ネクタイのパズル」 や 「財布のゲーム」 では問題文の中に数式や変数記号が書かれていない。
- 「ネクタイのパズル」 や 「財布のゲーム」 では、 二人のネクタイや財布の中身のたどった経緯や、 それらの価値の差や比が明確でない。 二人が同じ程度のお金持ちだということ以外に手がかりがないので、勝ち負けの確率
1/2 の重要性が高い。 - 問題文の中の 「手持ちの金額を失うかもしれないが、それ以上を得るかもしれない」 という表現は、 「変数の誤用」 の一歩手前の表現である。
負けるときは手持ちの金額を失う。
勝つときは手持ちの金額+α を得る。
手持ちの金額を X とすると損得は
(-X) + (X + α) = +α
だからこのゲームは自分に有利だ。
勝つときは手持ちの金額+α を得る。
手持ちの金額を X とすると損得は
だからこのゲームは自分に有利だ。
しかし、上記の 「ネクタイのパズル」 や 「財布のゲーム」 の問題文と 「二つの封筒問題」 の問題文との間には次のような違いがあるので、そうやすやすとは 「二つの封筒問題」 で 「変数の誤用」 が起こらないでしょう。
「ネクタイのパズル」 や 「財布のゲーム」 では期待値計算式抜きでパラドックスを発生させているが、
二つの封筒問題では期待値計算式を使ってパラドックスを発生させている。
(倍率の平均や加減算の錯覚 や 損得勘定での変数の誤用 を使って期待値計算式抜きでパラドックスを発生させている問題文を私は見たことがありません)
(倍率の平均や加減算の錯覚 や 損得勘定での変数の誤用 を使って期待値計算式抜きでパラドックスを発生させている問題文を私は見たことがありません)
パラドックスの源として書かれている期待値計算式を見てから、そこに書かれている
二つの封筒問題の歴史にもそぐわない
2014/05/11 に Nalebuff, Barry. (1988). から得た情報を元に、修正を加え、2014/11/24 に一部割愛しました。2015/04/05 に内容を整理しました。
Nalebuff, Barry. (1988). に、 彼の元に二つの封筒問題が届くまでの経路が書かれていて、それ以上さかのぼることは出来ないとしています。
Barry Nakebuff ← H. V. さん ← S. Zabell ← S. B. さん
Nalebuff, Barry. (1988). に出てくる 「アリさんに封筒を渡してからババさんに渡す封筒の金額を決める型」 の問題文が 「封筒を開けてから交換型」 であることと、 Zabell, S.L. (2005). の中に書かれている二つの封筒問題が 「封筒を開けてから交換型」 であることから、 Nalebuff さんに伝わった二つの封筒問題を遡った果ての問題が同じように 「封筒を開けてから交換型」 だった可能性があります。 Zabell, S.L. (2005). は Nalebuff さんに二つの封筒問題が伝わった 1988 年ごろから 17年程後の出版なので、参考程度にしかなりませんが · · ·
Zabell, S.L. (2005). の中に書かれている二つの封筒問題は次のような展開になっています。
- 二つの封筒の金額は x と 2x
- A が開けた封筒の金額は 10ドル
- 以下は A の考え
- 確率 50 % で他方の金額は x の方、つまり 5ドル
- 確率 50 % で他方の金額は 2x の方、つまり 20ドル
- 他方の封筒の期待金額は
(1/2) × 5ドル+(1/2) × 20ドル = 12.5 ドル
つまり、二つの封筒問題のパラドックスは、歴史的には、選んだ封筒の金額を含む二組の金額ペアを考慮したときのパラドックスとして出発したことになります。
Wikipedia(英語版)の "Two envelopes problem" の記事 (23:02, 29 April 2014 の版) によると、 1996年に数学者によって書かれた論文が 「変数の誤用説」 の先駆けだそうです。
つまり、歴史的には 「変数の誤用説」 は二つの封筒問題が世に出てから数年後に出て来た新参者ということになります。
スマリヤンが Smullyan, Raymond (1992). で 「スマリヤンの二つの文のパラドックス」 を編み出した時期の方が早そうなので、 「数学者」 スマリヤンが 「変数の誤用説」 を唱える 「哲学者」 たちをからかうために、「スマリヤンの二つの文」 を考えたという私の推測は間違いでしょう。 (← 2015/04/06 に表現を戻しました)
「変数の誤用説」 を唱える人は、自分自身の体験として語ることがない
私の印象にすぎないかもしれませんが、最初に期待値計算式の意味を理解したときの (自分の) 頭の中を思い出しても、
その中に A と 2A という二つの金額のイメージしか、思い出せない。
だから期待値計算式の意味を (自分は) 勘違いしていたのだろう。
といった具合に、 自分自身の体験談として語っている論文を見たことがありません。 (← 2014/05/11 に詳しく書き直しました)
期待値計算式 (1/2) (x/2) + (1/2) 2x を考えるときにも、 (x/2, x), (x, 2x) という二組の金額ペアは計算式の中にしかなく、頭の中には一組の金額ペアしかないはずだ。
といった具合に、 心理学説として語っている人も見かけたことがありません。 (← 2014/04/26 に書き加えました)
「変数の誤用現象」 を誘発するような問題文が作られていない
2014/05/11 にこの項を加えました。「変数の誤用現象」 が実際に起きるものなら、次のような 「変数の誤用現象」 をさらに起きやすくする問題文が考案されそうなものです。
例えば片方が 10 ドルでもう一方が 20 ドルとします。 そうすると確率 1/2 で選んだ方が 10 ドルでもう一方が 2倍の 20 ドルになり、 確率 1/2 で選んだ方が 20 ドルでもう一方が半分の 10 ドルになるので、 選んだ方を X ドルとしたときのもう一方の金額の期待値は (1/2) × 2X + (1/2) × (X/2) = 1.25 X となります。
しかしこのような 「変数誤用説におあつらえ向き」 の問題文を見たことがありません。
Zabell, S.L. (2005). の中に書かれている二つの封筒問題は次のような展開になっていて、「変数誤用説に 多少 おあつらえ向き」 な箇所もあります。
- 二つの封筒の金額は x と 2x
- A が開けた封筒の金額は 10ドル
- 以下は A の考え
- 確率 50 % で他方の金額は x の方、つまり 5ドル
· · · (1) - 確率 50 % で他方の金額は 2x の方、つまり 20ドル
· · · (2) - 他方の封筒の期待金額は
(1/2) × 5ドル+(1/2) × 20ドル = 12.5 ドル
2014/09/28 にこの箇所を書き足しました。
Wikipedia(英語版) でも、 「変数の誤用説」 の扱いに混乱が見られる
2014/05/15 にこの項を加えました。Wikipedia(英語版)の "Two envelopes problem" の記事 (23:02, 29 April 2014. の版) の冒頭部分は次のようになっています。
冒頭で "The problem" という語に続けてゲームのルールを記述。
"Example" の項で金額の具体例を上げるときに、選んだ封筒 20 ドル、交換して半分になったとき 10 ドル、交換して倍増したとき 40 ドル といった風に、 二組の金額ペアの具体例を明記。 · · · (1)
そのすぐ後に続く "Problem" の項で期待値計算式に至る過程を記号のみで、つまり具体的な金額の例なしに説明。
そのすぐ後に続く "Common Resolution" の項で 「変数の誤用説」 を説明。 · · · (2)
"Example" の項で金額の具体例を上げるときに、選んだ封筒 20 ドル、交換して半分になったとき 10 ドル、交換して倍増したとき 40 ドル といった風に、 二組の金額ペアの具体例を明記。 · · · (1)
そのすぐ後に続く "Problem" の項で期待値計算式に至る過程を記号のみで、つまり具体的な金額の例なしに説明。
そのすぐ後に続く "Common Resolution" の項で 「変数の誤用説」 を説明。 · · · (2)
上記の (1) と (2) が矛盾していることに気付いたのは私だけでしょうか?
「変数の誤用説」 の平均値版がある
2014/12/21 にこの項を加えました。Wikipedia(英語版)の "Two envelopes problem" の記事 (21:39, 23 November 2014 の版) の "Simple resolutions " の項に書かれている説の一つは、 選んだ封筒の金額も平均値で考えているものの 「変数の誤用説」 によく似ているので、それをザックリまとめると次のようになります。
- 期待値計算式の中の変数 A は A の平均値のつもりである。
- A が小さい方だったときの平均値と A が大きい方だったときの平均値の違いを忘れた。
このおまじないがデマだと示唆する事情もある
2015/05/10 に 「このおまじないがデマだと言い切れない事情もある」 という章を見直して 「このおまじないがデマだと示唆する事情もある」 という章として書き直しました。このおまじないの元祖とされる数学者はこのおまじないを唱えていない
Wikipedia(英語版)の "Two envelopes problem" の記事 (23:02, 29 April 2014 の版) に「変数の誤用説」 の先駆けとして載っていた論文の執筆者の職業を調べたら数学者でした。この事実は全く予想外で衝撃的だったため、このおまじないがデマだと自信を持って言えなくなりました。
長い間ネットで調べても彼の論文を読むことができなかったのですが、2015年になってやっと読むことができました。2015年の4月1日にこの論文のコピーをやっと手にいれることができました。 → 「変数の誤用説」 を唱えた数学者は二つの封筒問題を勘違いしていた?
彼も 「確率の錯覚」 を起こしていたであろう痕跡を論文の中に見つけることはできませんでしたが、 彼が自分の体験として語っている箇所も見当たりませんでした。
特筆すべきことは二組の金額ペアを考えることが原因で誤った期待値計算式が出来上がったと主張していることです。 (← 2015/09/23 訂正)
「変数の誤用」 の方は期待値計算式の誤りを説明するために副次的に取り上げられていました。
「変数の誤用説」を唱える多くの論文にこの論文が 「変数の誤用説」 の元祖として引用されているのは、誤解に基づいていたのです。
このおまじないを唱える心理学者は自分の仕事を忘れている
モンティ・ホール問題の確率の錯覚の研究で有名なある心理学者が二つの封筒問題について論文( (Google によると 2004/04/06 時点で引用件数 2))を書いていたので読んでみると、驚いたことに「二つの封筒問題のおまじないの王様」を力説していました。そんな論文を読んでしまったために、二つの封筒問題のパラドックスは確率の錯覚が原因だという説に対する自信が揺らいでしまいました。 「変数の誤用」 という心理現象を起こす人たちも実際に存在していて、この論文を書いた心理学者本人もその一人かも知れないと思ったのです。
その論文の内容
- 同じ変数記号が同じ値を表すと
A/2, A, 2A という三つの金額があることになるが封筒は二つなので、それはできない。 - A と 2A という二つの金額だけで計算するとパラドックスが解消する。
この心理学者は自分の仕事を忘れたらしい
彼女は二組の金額ペアを考えること自体がパラドックスの原因だと思い込んでしまったので、確率の錯覚現象の方にまったく目が行かなくなったのでしょう。
結局、おまじないとデマの合体したものではなくて、単なるデマなのかも知れない
2014/05/15 にこの項を加え、2014/11/24 に項のレベルを一つ上に上げ、2014/12/21 に表題を変えました。2015/04/05 内容を一部修正しタイトルも変えました。
このおまじないは次の二つの主張に分解することができます。
- 期待値計算式の中の変数記号が項によって異なる値を意味しているのは、変数の使い方の誤りである。
· · · (1) - 項によって変数が異なる値を意味していることに気付けば、二つの封筒の金額の期待値が二つの封筒の金額の平均に一致するので、二つの封筒が互角であることが確認できる。
· · · (2)
(2) の方は、(1) を説明するための補足ではなくて二つの封筒が互角であることを確認したい気持ちの表れ、すなわち 「おまじない」 ではなくて、 (1) がデマでないことを示すためにわざわざ (2) を示しているのかも知れません。
しかし、このおまじないがどんなに奇妙でも間違いを論証できない
2014/05/18 にこの項を設けて、「私が期待する心理学実験」 の項にあった記述をここに移動しました。このおまじないは上で見たように非常に奇妙ですが、 残念ながら現状では次のような理由から間違いを論証できません。
- 実際に「変数の誤用現象」 を来す人たちがいる可能性が心理学的に否定されていない。
- 選んだ封筒の金額を特定して論じる問題設定と、二つの封筒の金額のペアの方を特定して論じる問題設定は別箇の問題であるので、一方の結果をもってして他方の誤りを証明することはできない。
- 「選んだ封筒の中の金額を確率計算の条件とせよ」 と二つの封筒問題の問題文に書かれることはめったにない。
注:
2015/6/20 まで私は次のようなことも理由に含めていました。
½ × (x/2) + ½ × 2x という式の中の x が確率変数だとすると二つの項が同一の事象に関するものだということになってしまい、二つの項のそれぞれが、選んだ封筒が高額側である事象や少額側である事象に対応しているという共通理解に反してしまうので、確率変数を持ち出すこと自体が勘違いだということがわかります。 確率変数を持ち出す人たちは、½ × (x/2) + ½ × 2x の各項の変数記号 x が異なる確率変数に対応しているからおかしくなるのだという説を読んで、変数記号 x 自体が確率変数だと勘違いしたのでしょう。
(← 2015/08/29 に修正)
(参考: 「変数の誤用説」 を唱えた数学者は二つの封筒問題を勘違いしていた?)
2015/06/20 に私が Wikpedia で調べた範囲では、期待値計算式の中に確率変数が書かれている公式を見つけることはできませんでした。 そんなことからも 「期待値計算式の項が確率変数を表しているという説に一理あるかもしれない」 と思っていた私に知識不足の面があったことがわかります。
- 「開ける前に交換型」 の二つの封筒問題の場合、選んだ封筒の金額を表す 「記号」 の解釈にふた通りある。
一つは期待値計算式の 「中」 では通常の 「変数」 だとする解釈で、 もう一つは期待値計算式の 「中」 の 「確率変数」 だとする解釈である。
(参考: 「変数の誤用説」 を唱えた数学者は二つの封筒問題を勘違いしていた?)
2015/06/20 に私が Wikpedia で調べた範囲では、期待値計算式の中に確率変数が書かれている公式を見つけることはできませんでした。 そんなことからも 「期待値計算式の項が確率変数を表しているという説に一理あるかもしれない」 と思っていた私に知識不足の面があったことがわかります。
「おまじないの王様」 を唱える人の心理プロセスに関する仮説
2014/05/04 にこの項の書き方を修正して読みやすくしました。このおまじないを、ネット上記事で読んだり、論文で読んだりしているうちに、このおまじないを唱える人の共通点が浮かび上がってきました。
- 期待値計算式の中の変数記号が 「確率変数」 だと思っている人も、思っていない人も、同じ変数が項によって異なる値を表していると思っている。 「確率変数」 だと思っている人は、そのことがわかりやすくなるように式を書き換えたがるし、「確率変数」 だと思っていない人は、期待値計算式が根本的に間違っていると思っている。
- 論文などでは 「標準的期待値計算式」 という言葉を使いたがる人も見かける。
- (x/2, x) と (x, 2x) という二種類の金額ペアを同時に考えることを避けようとする。
- (a, 2a) という単一の金額ペアだけで済ますことに、何のてらいもない。 (x/2, x) と (x, 2x) という二種類の金額ペアを考えることは間違いだと主張する人すらいる。
- 金額ペアの確率分布に基づく数学的分析を理解できない。
- 「開けてから交換型」 より先に、「開ける前に交換型」 の二封筒問題を知ったらしい。
- 「変数の誤用」 を自分の体験として語っていない。
- 奇妙なほど自分の説に自信を持っている。 ( ← 2014/11/06 に加筆)
ある論文では、封筒が二つしかないから金額も二つしかないと述べていました。
もう一つの論文では、冒頭から二つの金額だけを変数で明記して議論を初めていました。
まだ私が知っている事例が少ないのですが、無視できません。 ← 2014/05/18 にこの文を加えました。
上記をふまえて、このおまじない (変数誤用説) を唱える人の心理プロセスについて仮説を考えてみました。
2015/04/05 に全体的に以下の記述を簡素化しました。
仮説 1-改々 【神の視点説+パラドックスを感じる人の心理に対するデマ説】 封筒の中の二つの金額を見ている神の視点に立ってしまい、そこから逃れることができない人たちがパラドックスを感じることができる人の心理を説明するために 「変数の誤用説」 を思いついた
2015/01/02 に 「仮説 1 【パラドックスを感じる人の心理に対するデマ説】」 「仮説 1-改 【神の視点説】 」 を合体させたものがこの項です。このおまじないを唱える人は 「単一金額ペアへの固執」 が強いのかも知れません。
そうなる理由としては、封筒のどちらかを選ぶ前の封筒の中身のイメージ、すなわち 「神の視点」 から逃れられないためかも知れません。
そして、封筒が二つだから金額の数も二つでなければならないという理論を思いついて、 数学が得意な人なら思いもよらない別種のパラドックスに行き着いたのかも知れません。
- 彼らは最初に二つの封筒の中の金額を A と 2A の二通りだと解釈する。
- その二つの金額を見ている 「神の視点」 から逃れることができない。
- 期待値 1.25 x を導く期待値計算式の間違い探しをする過程で、期待値計算式が
x/2, x, 2x という 3つの金額をが前提にしていることに気づく。 - A と 2A だけを使って期待値を計算しなおすと封筒を交換してもしなくても同等になるので、そうした考えが正しく、3つの金額を考える考え方は間違っていると勘違いする。
- そうした人たちの中でパラドックスの元になる期待値計算式が導かれた経緯を考えた人が、「変数の誤用説」 を思いつく。
- 「神の視点」 から逃れることができない人は、二組の金額ペアによる数学的な説明を読んでも理解できない。
彼らが単一の金額ペアのイメージに合わせて期待値の計算式を解釈するためには、彼らに次のような条件が必要でしょう。
- 最初に読んだ問題文が 「封筒を開ける前に交換型」 だった
- メンタルモデルの切り替えが困難 (頭が固い)
仮説 2 【自己欺瞞説】 彼ら自身も 「確率の錯覚」 を起こしていたことを忘れた
彼らも 「確率の錯覚」 を起こしていたのに、期待値の計算式のどこが間違っているか考えているうちに忘れてしまったのかも知れません。「確率の錯覚」 が特に強烈なため、期待値計算式の確率部分には全く目が行かなくて、苦し紛れに、変数の方に目を付けたのでしょう
彼らが 「確率の錯覚」 を忘れてしまうためには、彼らに次のような条件が必要でしょう。
- 最初に読んだ問題文が 「封筒を開ける前に交換型」 だった
- 確率の錯覚が特に強烈で、確率部分に全く目が行かない。 (← 2014/05/10 にこの行を追加しました)
- 期待値を考える前や考えた後は (A, 2A) という単一金額ペアのイメージしか頭になく、期待値を考えている間だけ (x/2, x) と (x, 2x) という二組の金額ペアを考えていた。 (← 2014/05/05 にこの行を追加しました)
仮説 2-改 【暗示に掛かった説】 「変数の誤用説」 を知って納得したために彼ら自身が 「確率の錯覚」 を起こしていたことを忘れた
2015/02/15 にこの項を加えました。仮説 2 【自己欺瞞説】で述べたような特性の人たちが 「変数の誤用説」 を読むと納得して暗示に掛かってしまうのかも知れません。 そして自分たちが変数の誤用を起こしていたと思い込んだのかも知れません。
仮説 2-改々 【二組の金額ペアを原因と勘違い説】 一度は期待値計算式を理解したものの金額 x/2 と 2x で期待値計算式を考えることがパラドックスの原因だと勘違いした
2015/03/29 にこの項を加え、2015/05/17 に表題を変えました。一度は期待値計算式を理解してパラドックスの存在を理解した人が、金額 A と 2A だけで期待値計算式を組み立てるとパラドックスが回避できることに気づいたために、金額 x/2 と 2x で期待値計算式を考えること、つまり二組の金額ペアを考えることがパラドックスの原因だと勘違いしたのかも知れません。
そして、一度は二組の金額ペアを考えていたこととの矛盾を解消するために、自分たちが変数の誤用を起こしていたと思い込もうとしているのかも知れません。
仮説 3 【変数の誤用実体験説】 数学が苦手なため変数の使い方が混乱し、別種のパラドックスを作りだした
2014/11/06 にこの項を加えました。彼らは数学が苦手で、特に変数に慣れておらず、期待値の概念もよく理解していないために混乱を来したのかもしれません。そして数学が得意な人なら思いもよらない別種のパラドックスに行き着いたのかも知れません。
- 彼らは変数が苦手なため、期待値計算式の二つの項を同時に理解することができない。
- そうして期待値計算式の項を一つ一つ理解しようとしたときに、変数に慣れていないため、同じ計算式の中の同じ変数記号に別の値を割り当ててしまう。
- 期待値に慣れていないので、同じ変数記号に別の値を割り当てたことが間違いであることに気が付かない。 「確率変数」 だから項によって異なる値でもおかしくないと思ったりする。
- そうして出来上がった期待値計算式が導いた期待値 1.25 x がパラドックスの元だと聞いて、何かが間違っていたと気づいても、 「単一金額ペアへの固執」 が強いため、確率 1/2 を疑うことも、二組の金額ペアを考えることもできない。
- 同じ変数記号に別の値を割り当てたことがパラドックスの原因だと解釈して安心する。 数学の得意な人なら最初から同じ変数記号に別の値を割り当てないことに気づかないし、彼らが解決したとするパラドックスが、数学の得意な人が感じるパラドックスとは別物であることにも気づかない。
- 「変数の誤用」 を誰もがすることだと思いこんだので、自分の体験談として語る必要を感じない。
仮説 4 【変数記号解釈原因説】 金額を表す変数が選んだ封筒が少額側か高額側かで異なる値をとりうるという解釈に誘導するような問題文だったため、別種のパラドックスに行き着いた
2015/01/01 にこの項を加えました。彼らが読んだ問題文に、選んだ封筒の金額と他方の封筒の金額を変数記号で表した式があって、それが 「方程式」 あるいは 「関係式」 に見えるような書き方だったのかも知れません。そして通常の問題文なら思いもよらない別種のパラドックスに行き着いたのかも知れません。
- 彼らが読んだ問題文に次のような記述があった。
「選らんだ封筒の金額を A で表し、他方の金額の封筒を B で表すと、確率 1/2 で B = A/2 、 確率 1/2 で B = 2A である。」 · · ·(1) - 彼らにはこれらの式が 「方程式」 あるいは 「関係式」 に見えてしまい、それぞれで A の値が異なると考えた。
- そのような解釈のため、期待値計算式
(1/2)A/2 + (1/2)2A の変数記号の使い方が誤っていると考えた。
Wikipedia(英語版)の "Two envelopes problem" の記事(21:39, 23 November 2014 の版)の "Introduction to further developments in connection with Bayesian probability theory" の項に書かれていた記述をヒントに、この仮説を思いつきました。
仮説 5 【E=(1/2)a + (1/2)2a が正解だと勘違い説】 単一金額ペア (a, 2a) で書いた期待値計算式がパラドックスを起こさないことに気づいて勘違い
2015/08/29 にこの項を加えました。
彼らは期待値計算式の意味をよく理解していないために、
E = (1/2)(x/2) + (1/2)2x から自らの体験としてパラドックスを感じることができない。 (期待値計算式に慣れていないか、変数の意味を理解できないか、あるいは他の原因で)- なんらかの理由で
E = (1/2)a + (1/2)2a という式ならパラドックスにならないことを知った。 E = (1/2)(x/2) + (1/2)2x はE = (1/2)a + (1/2)2a の書き間違いだと勘違いした。- 「スマリヤンの錯覚」 のために、これらの式がまったく別の問題に対する回答であることに気づかない。
- 自分の考えを正当化するために人によって次のような異なる道に進んだ。
- ある人たちは 「二組の金額ペア妄想説」 を唱える。
- ある人たちは 「変数の誤用説」 を唱える。
私が期待する心理学実験
上で見たように、「変数の誤用説」 を唱える心理について、いくつかの仮説が成り立ちます。 どの仮説が正しいのか、実験で検証する心理学者が現れることを望んでいます。実験で用いる問題文は次のような観点で変化をつけるとよいと思います。
- 「封筒を開ける前に交換型」 か 「封筒を開けてから交換型」 か
- 変数記号だけで期待値の計算を説明すか、具体的な金額を使って説明するか ( ← 2015/04/25 に加筆)
- 金額ペアの確率分布にばらつきがあることを明示しているか否か
- 期待値計算式を出す前に、しつこく単一金額ペアでの議論をするか、あっさりとすませるか
- 期待値計算式の意味を丁寧に説明するか、あっさりとすませるか
- パラドックスが存在することの説明を理解できるか否か?
- パラドックスの原因に関する説明のうち、どれに同意するか?
- 確率の勘違いが原因だとする説明
- 二組の金額ペアを考えたことが原因だとする説明
- 変数の誤用説
- その他
被験者を一旦、 「変数の誤用説」 に誘導しておいてから、その説では「封筒を開けてから交換型」の問題を解決できないことを示したときの被験者の反応も調べていただきたいと思います。 ← 2014/05/06 にこの文を追加しました。
被験者に 「交換して倍になったときと半分になったときの金額の比はどのくらいか」 という、スマリヤン的な質問をぶつけるのも良いと思います。
4 対 1 という回答が大勢を占めたら、 「変数の誤用説」 は常識的には誤り ということになりますが、
このおまじないを唱える人自身が確率の錯覚をしていたことが心理学実験で証明されれば、このおまじないは誤りであると結論できるでしょう。
「封筒を開ける前に交換型」 の二つの封筒問題でも、期待値計算式の中の記号が特定の値を表していると解釈する人の方が多いことが、心理学実験で証明されれば、このおまじないは 「常識的には」 誤りであると結論できるでしょう。 ← 2014/04/16 にこの文を書き換えました。
現時点での私の結論 · · · とりあえずの
この項を 2014/05/10、2014/11/06、2014/11/12、2015/02/15、2015/03/29、2015/05/17、2015/08/29 に書き直しました。「変数の誤用説」 を唱える人たちの心理を心理学者が実験で解明するまで、はっきりしたことを言えませんが、上記の私の仮説の中では次の仮説を最も有望視しています。
仮説 5 【E=(1/2)a + (1/2)2a が正解だと勘違い説】 単一金額ペア (a, 2a) で書いた期待値計算式がパラドックスを起こさないことに気づいて勘違い
この仮説が正しければ、この「二封筒問題のおまじないの王様」 は、それをを唱える本人を含めてだれも感じたことのない実在しない架空のパラドックスを解決しているのです。
まとめ
この 「二つの封筒問題のおまじないの王様」 を唱えることは、「選んだ封筒の金額に着目するところから二つの封筒問題が始まっていることを忘れる」 という非常に不思議な心理現象なので、ぜひそのメカニズムを解明したいものです。付録
このおまじないを唱える哲学論文の代表例
Clark, Michael. & Shackel, Nicholas. (2000). の中にパラドキシカル分布 に関して、次のような記述があります。この論文 (Clark, Michael. & Shackel, Nicholas. (2000).) では、一方の封筒の金額を条件とした期待利得を考えることには正当性を認めず、両方の封筒の金額ペアを条件とした期待利得を考えることだけに正当性を認めているようです。そして、「対称性」 や 「ゼロに等しい」 という理由以上の根拠が書かれていないようなので、この有名な論文も、私には 「二封筒問題のおまじないの王様」 に見えます。
余談
私が 二封筒問題のパラドックスたち で述べた 「神様視点のパラドックス」 に執筆者が罹っていることを思わせる記述もこの論文の中にあります。
「変数の誤用説」 を唱えた数学者は二つの封筒問題を勘違いしていた?
2015/04/26変数誤用説を最初に唱えたとされる数学者に論文を書かせるきっかけとなった別の論文を 2015/04/19 に読むこともできました。
その結果その数学者が二つの封筒問題を誤解している可能性に気づいたので表題を書き換えました。
同時に「二組の金額ペアを考えることが誤りの元だ」 という意見がこの論文の主たる主張であることに気づいたので内容の一部修正も行いました。
2015/9/5
その結果その数学者が二つの封筒問題を誤解している可能性に気づいたので表題を書き換えました。
同時に「二組の金額ペアを考えることが誤りの元だ」 という意見がこの論文の主たる主張であることに気づいたので内容の一部修正も行いました。
この数学者がどんな勘違いをしたか、ひらめきました。
Wikipedia(英語版) の "Two envelopes problem" の記事 (23:02, 29 April 2014 の版) に 「変数の誤用説」 の先駆けだと書かれている論文 (1996年) の執筆者が 「哲学者」 ではなくて 「数学者」 であることに 2014/05/04 に気付いて以来、関心を持っていました。
2015/04/01 にその論文のコピーを得ることができたので、さっそく読んでみました。 その内容を一言で言うと次のようになります。
【内容の1】主たる主張
期待値は二つの封筒から一つを選んだ時点で計算しなければならない。
期待値計算式に(1/2)(S/2) という項と (1/2)2S という項があるということは、片方の封筒にお金 S を入れて、残りの封筒に S/2 と 2S のどちらを入れようか決めようとしている時点の計算をしていることになる。 ← 2015/09/05 と 09/23に訂正
↑ 2015/04/19 にこれがこの論文の主たる主張であることに気づいきました。
期待値計算式に(1/2)(S/2) という項と (1/2)2S という項があるということは、片方の封筒にお金 S を入れて、残りの封筒に S/2 と 2S のどちらを入れようか決めようとしている時点の計算をしていることになる。 ← 2015/09/05 と 09/23に訂正
【内容の2】主たる主張の解説
できあがった期待値計算式について二つの封筒から一つを選んだ時点で考えると次のようにおかしなことになる。
← 2015/09/05 に訂正
もう一つの封筒の金額が確率 0.5 で S/2 だというとき、 Sは二つの金額の大きい方だ。(状況1)
もう一つの封筒の金額が確率 0.5 で 2S だというとき、Sは二つの金額の小さい方だ。(状況2)
したがって、期待値計算式にこの二つの状況のSが同時に書かれていることになってしまう。つまり、Sに対応する確率変数が項によって異なることになってしまう。 (← 2015/08/25 訂正)
もう一つの封筒の金額が確率 0.5 で S/2 だというとき、 Sは二つの金額の大きい方だ。(状況1)
もう一つの封筒の金額が確率 0.5 で 2S だというとき、Sは二つの金額の小さい方だ。(状況2)
したがって、期待値計算式にこの二つの状況のSが同時に書かれていることになってしまう。つまり、Sに対応する確率変数が項によって異なることになってしまう。 (← 2015/08/25 訂正)
【内容の3】reference point という独特の用語
2015/09/23 にこの項を加えました。
この論文では "reference point" という独特の用語が2か所で使われています。お金を封筒に入れる段階では最初の金額Sに対して次の金額がS/2でも2Sでもあり得ることを "reference point" という用語が示していると私は誤解して「視点の誤り」だの「着目した時点の誤り」だのと訳しましたが、どうやら間違いのようです。
次のような言い回しがあるので、同じ記号Sが変数の意味と確率変数の意味の両方を持っていることを指しているようにも思えますが、よくわかりません。
S の意味が reference point としての役割を持ちながら、同時に確率変数でもあることがこの錯誤のエッセンンスである。
この数学者は 「変数の誤用説」 を唱えていなかった。
上記の「主たる主張の解説」 の部分だけ読むと、この論文の著者が 「変数の誤用説」 を唱えているように思う人が多いでしょう。
しかしこの著者自身は「変数の誤用」がパラドックスの直接の原因だと思っていないことが、論文を読んでわかりました。
「二組の金額ペア」 によってできあがった期待値計算式に 「単一の金額ペア」 を当てはめて解釈すると 「変数の誤用」 が見いだせるのであって、「変数の誤用」 が間違った期待値計算式を作ったわけではなかったのです。
この数学者の勘違い
2015/9/5 にやっと、この数学者がどんな勘違いしたかひらめきました。
- この数学者が参考にした数学論文(著者S)の中で封筒にお金を入れる手順が次のように書かれていた。
- 一つの封筒に金額 S を入れる。
- 確率 1/2 で S/2 、確率 1/2 で 2S をもう一方の封筒に入れる。
- パラドックスを導く計算式
(1/2)S/2 + (1/2)2S の中の確率 1/2 が、お金を封筒に入れる手続きに現れた確率 1/2 をひきづっていると勘違いした。
Wikipdia(英語版)のデマ
Wikipedia(英語版) の "Two envelopes problem" の記事 (23:02, 29 April 2014 の版) の "Common resolution" の項に書かれている次の文は 「デマ」 なのだと、私は思っています。
「(変数誤用説による) 上記の解決法を最初に指摘したのはなにがし (この数学者) の1996 年の論文である。」
参考文献
-
Clark, Michael. & Shackel, Nicholas. (2000).
The Two Envelope Paradox, Mind Magazine (Vol 109.435.July 2000)
-
Kent G. Merryfield, Ngo Viet, and Saleem Watson (1997).
The Wallet Paradox
American Mathematical Monthly,104,1997,647–649.
-
Nalebuff, Barry. (1988).
Puzzles: Cider in Your Ear, Continuing Dilemma, The Last Shall be First, More.
Journal of Economic Perspectives, 2(2): 149–156.
-
Smullyan, Raymond (1992).
Satan, Cantor, and infinity and other mind-boggling puzzles.
Alfred A. Knopf. pp. 189–192. ISBN 0-679-40688-3.
日本語訳「スマリヤンの無限の論理パズル : ゲーデルとカントールをめぐる難問奇問」
レイモンド・スマリヤン著 ; 長尾確訳. 白揚社
-
Zabell, S.L. (2005).
Symmetry and Its Discontents
Cambridge University Press.
用語解説
-
パラドキシカル分布
選んだ封筒の金額を条件とする条件付き期待交換利得が常にゼロより大であるような金額分布を言います。
このような場合、封筒を開ける前の二つの封筒が互角であることと矛盾しないのか? と不思議になります。
-
スマリヤンの錯覚
私の造語です。
封筒を交換したらどうなるかを考えるときに、選んだ封筒の金額を条件として考えるやり方と、二つの封筒の金額の組み合わせを条件として考えるやり方が、同じ問題を考えているという錯覚です。
この錯覚に罹った人は、「二封筒問題のおまじないの王様」 を唱えたり、スマリヤンの二つの文のパラドックスに罹ったりします。
-
倍率の平均や加減算の錯覚
私の造語です。
倍率の分母の数値が同一でなければ倍率の和や差に意味がないことを忘れる心理です。
二つの封筒問題の期待値計算式を倍率の平均の計算式と解釈することもできるので、 二つの封筒問題のパラドックスが 「倍率の平均の錯覚」 に基づいている可能性もあります。
「財布のゲーム」 では、 負けたときと勝ったときの利得の差に着目していますが、 利得を倍率で表すこともできるので、 「財布のゲーム」 のパラドックスが 「倍率の加減算の錯覚」 に基づいている可能性もあります。
-
損得勘定での変数の誤用
私の造語です。
確率がイーブンのときに期待値を計算するときは、確率を考慮しないで損得勘定をすることが多いと思います。
このような場合には、得をするときの元になる金額と、損をするときの元になる金額が異なることを忘れてしまい、勝つときの利得 を X 、負けるときの損を X/2 で表して、ついつい、X + X/2 のように足し加えてしまうことが多いと思います。
二つの封筒問題の期待値計算式から確率を消して見ると損得勘定の計算式と解釈することもできるので、 二つの封筒問題のパラドックスが 「損得勘定での変数の誤用」 に基づいている可能性もあります。
「財布のゲーム」 では、 負けたときと勝ったときの利得の差に着目しているので、 「財布のゲーム」 のパラドックスが 「損得勘定での変数の誤用」 に基づいている可能性は高いです。· · · 確率の錯覚に基づいている可能性も低くはありませんが· · ·
-
変数の誤用
二つの封筒問題で封筒を交換した後の金額の期待値を計算するときに起こす、次のような錯覚現象です。
金額ペア(A, 2A) の A が確率1/2 で自分の封筒に入っていて、交換すると倍になる。2A も確率1/2 で自分の封筒に入っていて交換すると半分になる。 倍になったり半分になったりする前の金額をXとすると、交換した後の期待値は(1/2) 2X + (1/2) (X/2) だ。
このように、A や2A が無意識に一つの変数 X に混ざり合ってしまう現象です。
こういう現象が実際に人の頭の中で起きているのだ、という説が 二封筒問題のおまじないの王様 – 変数誤用説 – の中核をなしています。
-
二組の金額ペア妄想説
「二組の金額ペア (x/2, x) (x, 2x) を考えたから、誤った期待値計算式E = (1/2)(x/2) + (1/2)2x を思いついてしまっただ。そもそも単一の金額ペア (a, 2a) で考えないからいけないのだ。」 という説です。
「変数の誤用説」 と並んで、E = (1/2)a + (1/2)2a が正しい期待値計算式だとする説の双璧をなしています。
英語でネット検索すると、「変数の誤用説」 よりもこの 「二組の金額ペア妄想説」 信奉者の方が数が多そうです。 (2015/8/29現在)
-
確率の錯覚
二つの封筒問題で封筒を交換した後の金額の期待値を計算するときに起こす、次のような錯覚現象です。
金額ペア(A, 2A) の A が確率1/2 で自分の封筒に入っている。2A も確率1/2 で自分の封筒に入っている。 だから自分の封筒の金額を X とすると、 もう一つの封筒にX/2 が入っている確率も、2X が入っている確率も、 どちらも1/2 だ。
このように、(X/2, X) と (X, 2X) という二組の金額ペアを考えるときに、一組の金額ペア(A, 2A) を考えていたときの確率をそのまま当てはめてしまう現象です。
-
単一金額ペアへの固執
私の造語です。
封筒にお金が入れられた後では、封筒の中身の金額ペアが一種類に決まっているというイメージに囚われて、期待値を計算するときにも、一種類の金額ペアしか考えられない心理現象です。
この心理現象が起きると、手持ちの封筒の金額を x円に対して、(x円/2, x円) と(x円, 2x円) の二組の金額ペアを考えられなくなります。
トップページに戻る