トップページに戻る
モンティ・ホール問題の不思議さを拭い去るおまじないがちまたにあふれている。
これらの大事な共通点は数学的に無意味だということである。
数学的に無意味であるからこそ、おまじないとしての効き目が期待できるのである。実際、それらに数学的な意味があったとしたら 「頭で理解できても心で納得できない」 状態から抜け出すことはできないだろう。
このおまじないには、他のおまじないのような胡散臭さが無いので、おまじないに過ぎないことに気付くのは容易でない。
また、Wikipedia(英語版など各種言語)にも次のような図解で載っていたりするので、「おまじない」だと言うのも勇気がいる。
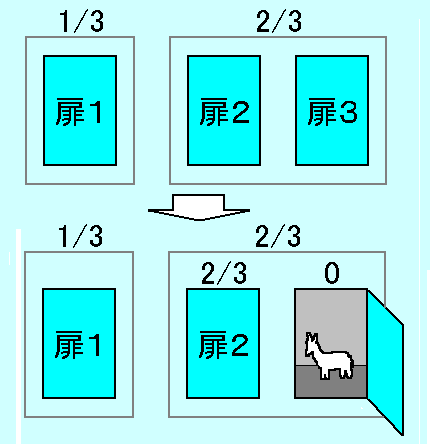
挑戦者が扉1 でなく扉2 を選んだ場合に対して同様な図を描くとこうなる。
この図がオリジナルの図よりやや分かりにくくなっていることも、もともと数学的に筋の通った説明でないことの表れだろう。
このおまじないを 「確率継承説」 と命名して、確率継承説の間違いで詳しく論じています。
補足
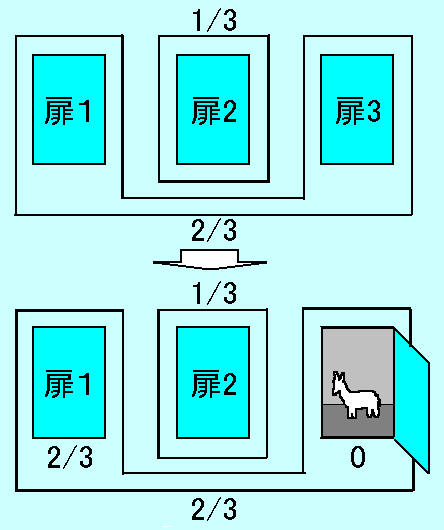
このおまじないには次のような親戚がある。
挑戦者が扉1を選んだ時点
扉1当たりの確率 = 1/3
扉2当りの確率 + 扉3当たりの確率 = 2/3
挑戦者が扉3を開けた時点
扉2当りの確率 + 扉3当たりの確率 は変わらない
扉3当たりの確率 = 0 と確定したので
扉2当たりの確率 = 2/3 - 0 = 2/3
図を使わず数式だけなので、これを読んで「確率継承説」だと気付くのに時間がかかる。
説明する人によって100万枚や100枚になる。
1990年の Marilyn vos Savant による説明が、そうした例の一つであり、その説明を要約すると次のようになる。
百万枚の扉があって、あなたが扉1を選んだと仮定してください。当たりの扉を絶対開けないホストが777,777番目の扉を残して全部開けたなら、あなたは777,777番目の扉に速攻で切り替えるでしょう?
扉の枚数が3枚であろうが百万枚であろうが数学的には全く違いが無いにも関わらず、扉の枚数が桁違いに多くなると switch が有利だという正解に納得する人が多くなることから、扉3枚と扉百万枚とでは認知心理学的に大きな違いがあることがわかる。
このおまじないを次のように言い換える人もいる。
百枚の扉があって、あなたが扉を1枚選んだと仮定してください。当たりの扉を絶対開けないホストが残りのうち98枚を開けてそれらがハズレであることを示したとき、最初に百枚の中から選んだ1枚が当たりの確率と、ホストが99枚の中から98枚を開けて残った1枚の当たりの確率はどちらが大きいでしょうか?
このような表現にすると 「確率継承説」 のおまじないも組み合わさっているのかも知れない。 残りの99枚をグループ化するイメージが強いからである。
このおまじないを唱える回答者をインターネットのQAサイトで見かけることがよくある。
このおまじないには、次のような変形がある。
2013/09/29 11:20:21
モンティ・ホール問題のおまじない
このページは 2013/03/07 に構成を大きく書き換えました。モンティ・ホール問題の不思議さを拭い去るおまじないがちまたにあふれている。
これらの大事な共通点は数学的に無意味だということである。
数学的に無意味であるからこそ、おまじないとしての効き目が期待できるのである。実際、それらに数学的な意味があったとしたら 「頭で理解できても心で納得できない」 状態から抜け出すことはできないだろう。
モンティ・ホール問題の答えに納得するためのおまじない
「ホストが開ける扉が挑戦者が選ばなかった範囲に限定されているので確率が継承される」と解釈するおまじない
私もこの解釈を長い間、信奉していたので、このおまじないリストに載せるのが遅れました。このおまじないには、他のおまじないのような胡散臭さが無いので、おまじないに過ぎないことに気付くのは容易でない。
また、Wikipedia(英語版など各種言語)にも次のような図解で載っていたりするので、「おまじない」だと言うのも勇気がいる。
挑戦者が扉1 でなく扉2 を選んだ場合に対して同様な図を描くとこうなる。
この図がオリジナルの図よりやや分かりにくくなっていることも、もともと数学的に筋の通った説明でないことの表れだろう。
このおまじないを 「確率継承説」 と命名して、確率継承説の間違いで詳しく論じています。
補足
このおまじないには次のような親戚がある。
挑戦者が扉1を選んだ時点
扉1当たりの確率 = 1/3
扉2当りの確率 + 扉3当たりの確率 = 2/3
挑戦者が扉3を開けた時点
扉2当りの確率 + 扉3当たりの確率 は変わらない
扉3当たりの確率 = 0 と確定したので
扉2当たりの確率 = 2/3 - 0 = 2/3
図を使わず数式だけなので、これを読んで「確率継承説」だと気付くのに時間がかかる。
「扉の数を100万枚に増やした場合」を想像するおまじない
扉の枚数を増やした場合を想像させて、扉を switch した方が有利であることを納得させようとする人たちをインターネットでよく見かける。このおまじないでご利益があった人、つまり不思議さが解消された人も多いらしい。説明する人によって100万枚や100枚になる。
1990年の Marilyn vos Savant による説明が、そうした例の一つであり、その説明を要約すると次のようになる。
百万枚の扉があって、あなたが扉1を選んだと仮定してください。当たりの扉を絶対開けないホストが777,777番目の扉を残して全部開けたなら、あなたは777,777番目の扉に速攻で切り替えるでしょう?
扉の枚数が3枚であろうが百万枚であろうが数学的には全く違いが無いにも関わらず、扉の枚数が桁違いに多くなると switch が有利だという正解に納得する人が多くなることから、扉3枚と扉百万枚とでは認知心理学的に大きな違いがあることがわかる。
私の仮説(1)
最初に選んだ扉1が当たりである確率が余りにも小さいので扉1が当たりである可能性は事実上ゼロに等しいと考え、その後で何が起きても扉1が当たりであることは考慮しないというヒューリスティクに基づいた判断かも知れない。もしそうだとすると宝くじを買うような人たちは扉百万枚の説明に納得しない人が多いかも知れない。私の仮説(2)
扉が3枚だけのときは、扉2が当たりだからホストが扉3を開けたということがそれほど強くイメージされないが、扉が百万枚のときは、扉777,777が当たりだから、それをうっかり開けないように注意しつつ残りの999,998枚を開けたという情景が強くイメージされるのかも知れない。つまり、多くの中から意図的に1つが選ばれたときには、あてずっぽう以外の要因を考えるというヒューリスティクがあるのかも知れない。このおまじないを次のように言い換える人もいる。
百枚の扉があって、あなたが扉を1枚選んだと仮定してください。当たりの扉を絶対開けないホストが残りのうち98枚を開けてそれらがハズレであることを示したとき、最初に百枚の中から選んだ1枚が当たりの確率と、ホストが99枚の中から98枚を開けて残った1枚の当たりの確率はどちらが大きいでしょうか?
このような表現にすると 「確率継承説」 のおまじないも組み合わさっているのかも知れない。 残りの99枚をグループ化するイメージが強いからである。
「どの扉が当たりか知っているホストがヒントを出してくれた」と解釈するおまじない
ホストがハズレ扉を開けたことはとりもなおさず、開け残した扉の当り易さに関するヒントになっていると解釈して安心しようとするのである。このおまじないを唱える回答者をインターネットのQAサイトで見かけることがよくある。
このおまじないには、次のような変形がある。
情報が与えられたことにより確率が変わる。
知識が増えたことによって確率が変わる。
「情報」に着目するおまじないは、vos Savant, Marilyn (1991).に見ることができて、 この中で Marilyn vos Savant は次のように考えることを提案している。
ホストがハズレの扉を開けた段階で、UFOが着陸して緑色の宇宙人(女)が出てきた。
ホストは残りの二つの扉のどちらかを指し示すよう宇宙人に頼んだ。
そして、「宇宙人が当りを指す確率が 1 / 2 であるのは、挑戦者と異なってホストがどちらの扉を開けたか知らないからだ」と述べている。
これらの呪文が数学的に無意味であることは、「ホストがヒントを出した」、「情報が与えられた」、「知識が増えた」などの言葉が「確率が変わった」と同義であることからわかる。
百歩ゆずって何がしかの情報がホストから与えられたとしても次のような情報である。
- ホストが扉を開けなかったり、当り扉を開けてしまったり、挑戦者が選んだ扉を開けてしまうようなことをしなかった。
- ホストが開けたのはこれこれの方であり、もう一つの方ではなかった。
Wikipedia(日本語版)の「モンティ・ホール問題」の最近の記事(22011年10月2日 (日) 09:17の版)の「2.3 最初にハズレのドアを選ぶ方法」の項にも、
「わざとハズレのドアを選べば、『モンティが、もう一つのハズレのドアがどれかを教えてくれる』」
という言い回しで、このおまじないが登場している。
「ホストが開け残した扉はホストに開けられるかも知れない試練を潜り抜けて来た」と唱えるおまじない
挑戦者が選んだ扉はホストによる試練を受けていないので当りやすさが小さいと言いたいのだ。このおまじないは 「確率継承説」 と似た面もあれば、 「ホストがヒントを出してくれた」 と唱えるおまじないと似た面もある。
「当たりでなくハズレを選んだつもりになる」おまじない
「最初にわざとハズレを選らぶ」という考え方をとると、switch する方が有利なことが理解しやすくなるという人を 2011年頃から見かけるようになった。(Wikipedia(日本語版)の「モンティ・ホール問題」の記事の「2.3 最初にハズレのドアを選ぶ方法」の項の影響かも知れない)最初に当たりを選んだつもりであろうとハズレを選んだつもりであろうと確率に何の影響もない。 このことは、Wikipedia(日本語版)の記事自体も 2011年6月15日 04:01 の版で認めている。
しかし、気持ちの上では大きな違いがあるのかも知れない。私がおまじないに分類する所以である。
これに似たやり方に「 switch すると最初から心に決める」方法がある。大同小異かも知れないが、私にはこちらの方がなじめる。
【余談】
最初の当たり扉の配置が均等ではなくて、かつ挑戦者がその確率を予想できるような状況であれば、最初に最もハズレそうな扉を選ぶのが最も有利な戦略になる。
決定木を使う方法にはおまじないの側面があるやも
この部分を 2013/08/16 に加えました。決定木を使ってモンティ・ホール問題を説明する方法がある。
①残った扉の当たり易さでなく、扉を替えたときの結果に着目していることと、②確率でなく賞品の価値を金額に置き換えた期待値を計算していることが特徴である。 これらの特徴には、扉を替えるか否かという戦略に着目すれば、ホストが扉を開けた後の確率に惑わされなくてすむという意味があるのかも知れない。
賞品の価値を例えば1リンカーンとか、1ベンツのように 1 と置いたら、期待値と確率は同じことになる。
決定木を持ち出すことには、確率概念から目をそらしてモンティ・ホール問題の不思議さから逃れるおまじないの側面もありそうである。
確率が 1 / 2 だと錯覚させた無意識の確率判断能力への信頼を取り戻すためのおまじない
問題の設定を変えたり、確率判断する人の視点を変えたりすると switch して賞品を得る確率が 2 / 3 ではなく 1 / 2 になることを論じることを好む人が多い。1 や 0 、あるいはその他の半端な確率は好まれないので、無意識の確率判断が直感的に導き出した 1 / 2 という数値と一致することに意味があるらしい。
「ゲームの途中に来た宇宙人にとっては確率が 1 / 2 になる」と唱えるおまじない
「『どの扉が当たりか知っているホストがヒントを出してくれた』と解釈するおまじない」 の項で述べたUFOから降り立った宇宙人のおまじないには 「確率が 1 / 2 だと錯覚させた無意識の確率判断能力への信頼を取り戻すためのおまじない」 としての側面もある。マリリン・ヴォス・サヴァント著 「気がつかなかった数学の罠 論理思考トレーニング法」 東方雅美訳 中央経済社刊 (2002) を読むと、彼女に反論する人たちをなだめるためにこの説明を出したらしいことがわかる。
番組の途中でUFOから降り立った宇宙人にとっては通常と同じように残った扉の当る確率が等しくなって安心するのである。
しかし、数学の確率概念に従って冷静に考えれば、決して通常と同じようにして確率が等しくなったのではない。
次のように
【
当り扉、挑戦者の選択、ホストが開ける扉で構成される 3次元の標本空間
【宇宙人の出現後の標本空間
(ゲーム開始時点から継続する標本空間)
緑色の宇宙人(女)が現れたことによって、当り扉、挑戦者の選択、ホストが開ける扉に宇宙人が選んだ扉が加わった 4次元の標本空間
【宇宙人の出現後の標本空間
(宇宙人出現時点から始まる標本空間)
当り扉と宇宙人の選択という 2次元の標本空間
ひとたび宇宙人がくれば通常の 1 / 2 と 1 / 2 の組合せに戻るという考え方は数学の確率概念と根本的に異なっている。
直感が導いた確率と一致するような条件を論じるおまじない
モンティ・ホール問題や3囚人問題の問題文の曖昧さを議論することを 「ワーディングの議論」 とよぶ。純粋な気持ちでワーディングを論じるのであれば、
「モンティ・ホール問題や 3囚人問題の問題文は "Well Defined"でないから答えは無い」 としたり、
「0 から 1 までの任意の実数 p について、求める事後確率 = p となるように素事象の確率を設定することができる」 としたりするはずである。
しかし実際には 標準仮定 の一部を取り上げて論じることが多く、中でも switch して賞品を得る確率が 1/ 2 になる条件を論じる人が多い。
このような議論には、確率 1 / 2 をはじき出した無意識の確率判断能力への信頼感を取り戻す効果があるのかも知れない。
Marilyn vos Savant に多くの数学博士たちが反論した原因を問題文の曖昧さのせいにするおまじない
「開け残された二つの扉が当りである確率はどちらも 1/ 2 だと多くの数学博士たちが勘違いしたのは問題文の曖昧さのせいだ」 という人がいる。 Craig F. Whitaker さんが Marilyn vos Savant に出題した問題文を 「ホストがハズレの扉を開ける可能性がある」 という風に解釈したら数学博士たちの答えで正しいということを根拠にしている。こういった説がデマであることは、 ドナルド・グランバーグ著 「モンティ・ホール・ジレンマ ‐変えるべきか 変えざるべきか‐」 を読めばすぐに分かる。
マリリン・ヴォス・サヴァント著 「気がつかなかった数学の罠 論理思考トレーニング法」 東方雅美訳 中央経済社刊 (2002) の巻末に付録として載っていて、日本語で読みやすい。
それはともかくとしてここでは、このような説を唱える人の心理に着目したい。 モンティ・ホール問題を間違えた人が自分の判断力に自信を取り戻すためにこういった説にすがっているのかも知れない。
モンティ・ホール問題は 「ひっかけ問題」 だと唱えるおまじない
これは、 「挑戦者が選んだ扉がハズレの確率が switch して当たる確率だ」 という説明をモンティ・ホール問題の全貌だと勘違いしたり、 上記の 「確率継承説」 に納得した人がモンティ・ホール問題は 「簡単な確率の問題」 だと勘違いして流すデマにすぎないのかも知れない。モンティ・ホール問題の簡単そうな説明を聞いて理解したつもりになった人が、日常の確率概念と数学の確率概念の隔たりに悩むという体験をしなかったとすれば、そういう人がこういうデマを流してもおかしくない。
しかし、このデマにはおまじないとしての効用もあるのではないかと、私は思う。
日常の確率概念と数学の確率概念の隔たりに悩んでいないふりをするために、こういうデマを流しているのかも知れないからである。
このおまじないには 「モンティ・ホール問題は簡単な確率の問題だ」 と唱える変形版もある。
日常的確率概念から数学的確率概念に乗り換える心理的抵抗を薄めるおまじない
日常的確率概念では扉自体に確率が割り当てられると考えるが、数学の確率概念では、標本空間の上の事象に確率が割り当てられていると考える。言い換えると、日常的確率概念では三つの扉で構成される一次元のメンタルモデルを考えていて、数学の確率概念では、当り扉の次元とホストが開ける扉の次元で構成される二次元のメンタルモデルを考える。
注:ここでは挑戦者が選ぶ扉を固定して考えています。
日常的確率概念のメンタルモデルから数学の確率概念のメンタルモデルに頭を切り替えればモンティ・ホール問題の答えを理解できるようになるはずであるが、そこには大きな心理的抵抗があるらしい。
この心理的抵抗を薄めるためのおまじないとして、次のようなものがある。
「ホストが当りの扉を知っていることに気付くことがモンティ・ホール問題を解く鍵だ」と唱えるおまじない
インターネットで見かけるモンティ・ホール問題の説明で、 このおまじないを唱えていることがよくある。このおまじないをとなえると、日常的確率概念のメンタルモデルの上にホストの行動という次元を掛け合わせて、数学的なメンタルモデルを構成することができるのだろう。
このおまじないによく似た例を数学者エルデーシュののエピソードに見ることができる。
ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月) にエルデーシュがモンティ・ホール問題で悩んだエピソードが書かれているので、要約すると次のようになる。
・ヴァージョニがモンティ・ホール 問題を話題にしたところ、エルデーシュはswitchする方が有利であるという結論に反対した。
・ヴァージョニが決定木を使って説明しても納得しなかった。
・ヴァージョニがパソコンを使ってモンテカルロ法でシミュレーションしたらエルデーシュは自分の間違いを認めたが、数学的な説明としては満足しなかった。
・ヴァージョニとのやりとりの後、グラハムがエルデーシュに次のように説明したところようやく納得した。
「司会者がかならず別のドアに変えるチャンスをくれるということをあらかじめ知っていることが鍵になるんだ。
それが問題を解くときに考慮に入れておかなければならないゲームのルールのひとつだ」
---ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月)
それが問題を解くときに考慮に入れておかなければならないゲームのルールのひとつだ」
---ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月)
※私の注 : ヴァージョニ(Andrew Vázsonyi)やグラハム(Ronald Graham)はエルデーシュの友人の数学者
このエピソードから数学的な説明では満足できないエルデーシュが、数学とは次元の異なる 「おまじない」 を求めていたことがわかる。 「考慮に入れておかなければならないゲームのルール」 という言葉の力で、 日常的確率概念のメンタルモデルから数学的な確率概念のメンタルモデルへの乗り換えの抵抗が薄れるのだろう。
上記のグラハムの説明の中で 「変えるチャンスをくれるということをあらかじめ知っていることが鍵になる」 とも述べているので、次に述べる 「主観確率」 を持ち出すおまじないの原型としての面もある。
数学の確率論では、モンティ・ホール問題を解く者が理解しているルールに従ってホストが行動すればよいのであって、挑戦者がルールを事前に知っているかどうかを問わないからである。
モンティ・ホール問題が挑戦者がルールを事前に知っているかどうかを意識するような問題だとしたら、 挑戦者から見た確率を問う問題になってしまう。 そして挑戦者がルールが知らない場合に ホストのルールをどのように予測するだろうかという、数学というよりは行動経済学の問題になってしまうか、 あるいはその予測に応じてどのような戦略を選択するかという、ゲーム理論の問題になってしまう。
ヴァージョニの著述によると、彼の決定木の説明が非条件付確率の問題設定 によるものであることから、モンテカルロ法による説明もそうであるに違いない。
扉3 が開けられた後にどの扉が開けられたか忘れなさいと言われても普通はできないから、いくら天才エルデーシュでも 非条件付確率の問題設定 を理解できなくて不思議はない。
グラハムの説明はおまじないとしての力と共に、 条件付確率の問題設定 に引き戻す力も持っていたのかも知れない。
こうした不思議さや気味悪さを振り払うおまじないを見つけたのでご紹介する。
「主観確率」 (subjectivist probability) とか 「客観確率」 (objective probability) といった確率解釈論 (probability interpletations) 用語を持ち出して、モンティ・ホール問題の確率は 「主観確率」 の方であり、「客観確率」でないから不思議なのだと唱える人がいる。
あるいはモンティ・ホール問題に限らず、一般の「事後確率」に関して、「事後確率」は「主観確率」だから、不思議なのだと唱える人がいる。
しかし、「主観確率」 の対立概念の 「客観確率」 の数学的な定義を私は見たことがない。
「事後確率」 を 「主観確率」 と呼びなおす定義なら見たことがあるが、そうしたところで何も得られない。「事後確率」 が未来から過去を予測する一風変わった確率であることは 「事後確率」という言葉の中に最初から含まれているからである。
それゆえ、「モンティ・ホール問題の確率は 客観確率でなく主観確率だ」 とか 「事後確率は主観確率だ」 と唱えることもおまじないの一種である可能性がある。
これらのおまじないは、モンティ・ホール問題や3囚人問題を数学的に解明しても一向に不思議さが消えないもどかしさを、哲学の力で払拭しようとしているのだろう。
モンティ・ホール問題を論じるときに 「主観確率」 を持ち出す人が多い理由について、「主観確率を論じたくなるわけ」 で仮説を述べてみました。
しかし、 モンティ・ホール問題を解くときには 「事後確率」 でなく 「尤度」 などの別の概念を用いるべきだと、統計数学に詳しい人が説明しているのを見たことがある。
「尤度」 は本来、 仮説事象を条件とする証拠事象の条件付き確率を表す用語なので、 このような説明をする人は 「尤度」 の意味を勘違いしている可能性がある。
ともあれ、「事後確率は確率に似ているが確率ではない」 と唱えれば、未来から過去を予測する 「事後確率」 が気味悪くなくなるのだろう。
「事後確率は確率にあらず」 と唱えることもおまじないの一種に違いない。
モンティ・ホール問題の問題文の曖昧さ(ワーディング)に目をつけて、標準仮定以外の可能性も考慮しなければならないと主張する人もいる。
そういう人たちがワーディングを論じる動機はさまざまである。
無意識の仮定 という心理現象の方を重視することで、 確率の錯覚 という心理現象の存在を忘れることができるのだろう。
「頻度確率」 という言葉を使う人は 条件付確率の問題設定 での解を 「ベイズ確率」 と呼んでいることも多い。
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). を皮切りに、モンティ・ホール問題を研究する統計数学者の間で長年使われている 「非条件付確率」 という用語を知らなかったり、 「頻度確率」 が 「ベイズ確率」 と対比的に使われる言葉であることに影響されたために、「頻度確率」 という用語を使い始めたのかも知れないが、 非条件付確率の問題設定での解と、条件付確率の問題設定 での解が並存する気味悪さを払おうとしているのかも知れない。
トップページに戻る
このエピソードから数学的な説明では満足できないエルデーシュが、数学とは次元の異なる 「おまじない」 を求めていたことがわかる。 「考慮に入れておかなければならないゲームのルール」 という言葉の力で、 日常的確率概念のメンタルモデルから数学的な確率概念のメンタルモデルへの乗り換えの抵抗が薄れるのだろう。
上記のグラハムの説明の中で 「変えるチャンスをくれるということをあらかじめ知っていることが鍵になる」 とも述べているので、次に述べる 「主観確率」 を持ち出すおまじないの原型としての面もある。
補足 1
上記の 「司会者がかならず別のドアに変えるチャンスをくれるということをあらかじめ知っていること」 という表現の主語が問題を解く者でなく、ゲームの挑戦者であったとしたら、また別種のおまじないになる。数学の確率論では、モンティ・ホール問題を解く者が理解しているルールに従ってホストが行動すればよいのであって、挑戦者がルールを事前に知っているかどうかを問わないからである。
モンティ・ホール問題が挑戦者がルールを事前に知っているかどうかを意識するような問題だとしたら、 挑戦者から見た確率を問う問題になってしまう。 そして挑戦者がルールが知らない場合に ホストのルールをどのように予測するだろうかという、数学というよりは行動経済学の問題になってしまうか、 あるいはその予測に応じてどのような戦略を選択するかという、ゲーム理論の問題になってしまう。
補足 2
上記のエルデーシュの行動の説明として、彼がおまじないを求めていたという説の他に、彼が 非条件付確率の問題設定 を理解できなかったという説も考えられる。ヴァージョニの著述によると、彼の決定木の説明が非条件付確率の問題設定 によるものであることから、モンテカルロ法による説明もそうであるに違いない。
扉3 が開けられた後にどの扉が開けられたか忘れなさいと言われても普通はできないから、いくら天才エルデーシュでも 非条件付確率の問題設定 を理解できなくて不思議はない。
グラハムの説明はおまじないとしての力と共に、 条件付確率の問題設定 に引き戻す力も持っていたのかも知れない。
モンティ・ホール問題の不思議さや、事後確率一般の気味悪さを振り払うためのおまじない
モンティ・ホール問題の不思議さが時がたつにつれて薄れていった後でも、扉が並んでいる情景を思い浮かべながら確率について考えていると不思議さが蘇ってくることは、私自身の体験から間違いない。こうした不思議さや気味悪さを振り払うおまじないを見つけたのでご紹介する。
「主観確率」 を持ち出すおまじない
注:私は
モンティ・ホール問題に絡めて「主観確率」 「客観確率」 を論じている人の「心理」に注目しているのであって、
それらの概念自体に異を唱えているのではないことにご注意されたい。
「主観確率」 (subjectivist probability) とか 「客観確率」 (objective probability) といった確率解釈論 (probability interpletations) 用語を持ち出して、モンティ・ホール問題の確率は 「主観確率」 の方であり、「客観確率」でないから不思議なのだと唱える人がいる。
あるいはモンティ・ホール問題に限らず、一般の「事後確率」に関して、「事後確率」は「主観確率」だから、不思議なのだと唱える人がいる。
しかし、「主観確率」 の対立概念の 「客観確率」 の数学的な定義を私は見たことがない。
「事後確率」 を 「主観確率」 と呼びなおす定義なら見たことがあるが、そうしたところで何も得られない。「事後確率」 が未来から過去を予測する一風変わった確率であることは 「事後確率」という言葉の中に最初から含まれているからである。
それゆえ、「モンティ・ホール問題の確率は 客観確率でなく主観確率だ」 とか 「事後確率は主観確率だ」 と唱えることもおまじないの一種である可能性がある。
これらのおまじないは、モンティ・ホール問題や3囚人問題を数学的に解明しても一向に不思議さが消えないもどかしさを、哲学の力で払拭しようとしているのだろう。
モンティ・ホール問題を論じるときに 「主観確率」 を持ち出す人が多い理由について、「主観確率を論じたくなるわけ」 で仮説を述べてみました。
「事後確率は確率ではない」と唱えるおまじない
確率論の立場から 「事後確率」 を考えると、確率論の公理を満たしているので立派な確率である。しかし、 モンティ・ホール問題を解くときには 「事後確率」 でなく 「尤度」 などの別の概念を用いるべきだと、統計数学に詳しい人が説明しているのを見たことがある。
「尤度」 は本来、 仮説事象を条件とする証拠事象の条件付き確率を表す用語なので、 このような説明をする人は 「尤度」 の意味を勘違いしている可能性がある。
ともあれ、「事後確率は確率に似ているが確率ではない」 と唱えれば、未来から過去を予測する 「事後確率」 が気味悪くなくなるのだろう。
「事後確率は確率にあらず」 と唱えることもおまじないの一種に違いない。
ワーディングを論じるおまじない
2013/09/29 にこの項を追加しました。モンティ・ホール問題の問題文の曖昧さ(ワーディング)に目をつけて、標準仮定以外の可能性も考慮しなければならないと主張する人もいる。
そういう人たちがワーディングを論じる動機はさまざまである。
- 数学の問題文として明確化したい。 (几帳面な人)
- 条件付確率の問題設定の場合、条件の違いが大きく効いてくることを確認したい。 (数学好きな人)
- 問題文の曖昧さが確率の錯覚に影響するのかしないのか、心理学実験したい。 (認知心理学者や教育心理学者)
- 人間には明記されていない条件を無意識に仮定する傾向があるので、確率が関係する事件に際して注意したい。 (行動経済学者や弁護士)
- など
無意識の仮定 という心理現象の方を重視することで、 確率の錯覚 という心理現象の存在を忘れることができるのだろう。
新手のおまじない候補
2012年ごろから、モンティ・ホール問題の非条件付確率の問題設定での解を、 「頻度確率」 ("frequentist probability") と呼ぶ人をインターネット上で見かけるようになった。「頻度確率」 という言葉を使う人は 条件付確率の問題設定 での解を 「ベイズ確率」 と呼んでいることも多い。
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). を皮切りに、モンティ・ホール問題を研究する統計数学者の間で長年使われている 「非条件付確率」 という用語を知らなかったり、 「頻度確率」 が 「ベイズ確率」 と対比的に使われる言葉であることに影響されたために、「頻度確率」 という用語を使い始めたのかも知れないが、 非条件付確率の問題設定での解と、条件付確率の問題設定 での解が並存する気味悪さを払おうとしているのかも知れない。
用語解説
-
標準仮定
モンティ・ホール問題や3囚人問題を数学的に解くためには問題文に明示的に書かれていない条件を仮定する必要がある。
標準仮定はそうした仮定の一つであり、モンティ・ホール問題の場合、次のような内容となっている。
①当たり扉はランダムかつ等確率に設定される
②ホストは挑戦者の選んだ扉を開けない
③ホストは必ず残りの扉を一枚開ける
④ホストはハズレの扉しか開けない
⑤ホストは挑戦者の選んだ扉が当たりのとき、ハズレ扉をランダムかつ等確率に選んで開ける
⑥ホストは扉を開けた後に必ずswitchの機会を挑戦者に与える
1975年に モンティ・ホール問題を発案した Steve Selvin も、
1990~1991年に PARADE誌のコラム"Ask Marilyn"で論争した人々の多くも、
標準仮定のもとに議論していた。
「標準仮定」(the standard assumptions)とは Wikipedia(英語版)の "Monty Hall problem"の記事で導入された言葉である。
-
条件付確率の問題設定
ホストが「これこれ」のハズレ扉を開けたということを証拠事象として、
「それぞれ」の扉が当たりである条件付き確率を計算する問題設定である。
-
非条件付確率の問題設定
ホストが「いずれか」のハズレ扉を開けることは最初から分っていることとして
(相場用語なら「織り込み済み」だとして)
「挑戦者が選んだ」扉、あるいは「残りの」扉が当たりである確率を計算する問題設定である。
参考文献
-
ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月)
原タイトル:The man who loved only numbers。
2000年4月の単行本の文庫版。
-
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991).
"Let's Make A Deal: The player's dilemma,"
American Statistician 45: 284-287.
-
vos Savant, Marilyn (1990).
"Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
-
vos Savant, Marilyn (1991).
"Ask Marilyn" column, Parade Magazine p. 12 (17 February 1991).
トップページに戻る