トップページに戻る
2008年ごろに、ある本でモンティ・ホール問題 (モンティホールジレンマ) を知り、
自分なりの解法を編み出しても不思議さが一向になくならないので、モンティ・ホール問題にはまってしまいました。
それ以来、モンティ・ホール問題や3囚人問題について調べて来た成果として、
条件付確率や事後確率の話題、
確率の錯覚に関する認知心理学の話題、
モンティ・ホール問題の歴史、 等々
をご披露します。
改訂の記録
2011/11/03にこのページを作って以来、ちょくちょく書き直しています。主要な改訂内容については、「モンティ・ホール問題と3囚人問題」改訂の記録 をごらんください。
2018/10/16 6:16:50
初版 2011/11/12 23:38:20
モンティ・ホール問題と3囚人問題
ご注意: このページはパソコンでの閲覧を前提として書いています。
はじめに
モンティ・ホール問題や3囚人問題は、確率に関する数学パズルである。
(「3囚人問題」は、「囚人のディレンマ」というゲーム理論の問題とは別物)
モンティ・ホール問題と3囚人問題は数学的構造が同一なため、数学や心理学の世界では同一視されることが多い。
条件付確率や事後確率の知識が無ければ、ほぼ確実に解けない問題でありながら、ほとんどの人が答えは自明だと錯覚し、直感的に間違った答えを出し、正解を教わって頭で理解しても心では信じられないという特徴を持っている。
確率計算の対象である「事象」のとらえ方によっては、等確率の場合の数を数える素朴な解き方で解けるので、そうした解き方を工夫する楽しみも人気のもとになっている。
数学の世界では、ちまたでの人気の割りに条件付確率や事後確率の例題としてさほど重視されていない。
心理学の世界では、確率判断の認知心理学、あるいは確率の錯覚の研究材料として盛んに利用されている。
Wikipedia(英語版)の"Monty Hall problem" の記事を見ても、2015年になっても相変わらず頻繁に更新されているので、人気の根強さ がわかる。(「はまっている人が多い」と言い換えることもできる)
これらの問題の骨格だけ述べると次のようになる。
(「3囚人問題」は、「囚人のディレンマ」というゲーム理論の問題とは別物)
モンティ・ホール問題と3囚人問題は数学的構造が同一なため、数学や心理学の世界では同一視されることが多い。
条件付確率や事後確率の知識が無ければ、ほぼ確実に解けない問題でありながら、ほとんどの人が答えは自明だと錯覚し、直感的に間違った答えを出し、正解を教わって頭で理解しても心では信じられないという特徴を持っている。
確率計算の対象である「事象」のとらえ方によっては、等確率の場合の数を数える素朴な解き方で解けるので、そうした解き方を工夫する楽しみも人気のもとになっている。
数学の世界では、ちまたでの人気の割りに条件付確率や事後確率の例題としてさほど重視されていない。
心理学の世界では、確率判断の認知心理学、あるいは確率の錯覚の研究材料として盛んに利用されている。
Wikipedia(英語版)の"Monty Hall problem" の記事を見ても、2015年になっても相変わらず頻繁に更新されているので、人気の根強さ がわかる。(「はまっている人が多い」と言い換えることもできる)
これらの問題の骨格だけ述べると次のようになる。
モンティ・ホール問題
|
3つの扉の1つに賞品が隠されていて、挑戦者が扉を1つ選ぶと、ホストが残りの扉のうちハズレである扉の1つを開け、
挑戦者に扉を選び直す機会が与えられるゲームがある。
ホストが扉を開けた段階で、選択を変更しない場合とした場合とで、賞品を獲得する確率はそれぞれどうなるか?
(答えは 1/3 と 2/3) |
3囚人問題
|
3人の囚人の誰か一人が恩赦になると囚人たちは知っている。一人の囚人が自分以外の処刑される囚人の名を一人だけ教えてくれと看守に頼んだら、
看守がだれそれが処刑されると答えた。質問した囚人と、看守が名を上げなかった残りの囚人の恩赦になる確率はそれぞれどうなるか?
|
モンティ・ホール問題と3囚人問題の概要
確率を錯覚する理由の手っ取り早い説明
「残った扉が当たりである確率や残った囚人が恩赦である確率は等しい」と多くの人が錯覚する。
驚くべきことに、「有名な数学の問題だ」と事前に言われても錯覚する人が多い。
このような錯覚心理を説明する主要な心理学理論は次の二つである。
驚くべきことに、「有名な数学の問題だ」と事前に言われても錯覚する人が多い。
このような錯覚心理を説明する主要な心理学理論は次の二つである。
- 問題構造の把握失敗 (不適切なメンタルモデル形成) 説
- 比率保存のヒューリスティク説
問題構造の把握失敗 (不適切なメンタルモデル形成) 説
確率を考えるとき、本来、標本空間の上の事象の持つ量としてとらえなければならない。
分かりやすく言うと、場合分けをして、それぞれの場合に確からしさを付与してから、問題を考えなければならない。
そして、モンティ・ホール問題や 3囚人問題を考えるときは、次のように場合分けをした上で確率を考えなければならない。
モンティ・ホール問題の場合は、どの扉が当りか、挑戦者はどの扉を選んだか、ホストはどの扉を開けたか、という観点を組み合わせて場合分けしなければならない。
3囚人問題の場合は、どの囚人が恩赦か、どの囚人が質問したか、看守はどの処刑囚人の名を上げたか、という観点を組合せて場合分けをしなければならない。
ところが、モンティ・ホール問題や3囚人問題の確率を錯覚する人たちは、このような多次元の空間で確率を考えないで、単に扉の配列や囚人の配列のような一次元の空間の上で確率を考えてしまう。
そのために確率を錯覚するのだ、というのが 「問題構造の把握失敗説」である。
Johnson-Laird, P. N., Legrenzi, P., Girotto, V., Legrenzi, M. S., & Caverni, J.-P. (1999). 、 Tubau, E. & Alonson, D. (2003). などが代表的な研究者である。
2014/10 に下記のように 「事象」 と 「現象」 の区別について補筆しました。
私は 「事象」 と 「現象」 の区別がついていないことがこのような 「問題構造の把握失敗」 の背景にあると思っている。
標本空間を素事象に分割し、確からしさを素事象に配分し、素事象を分類し、それぞれの分類に含まれる素事象の確からしさの総計を比較したものが確率であるという確率論の基本を教わる人は、理科系の学生でも少なそうである。 (2014年現在)
そのため、中学や高校で 「場合分け」 してから 「場合の数」 で確率を計算する方法を教わっただけの人たちは、 「場合分け」 が 「確率」 を計算する 手段だと誤解してしまうのだろう。
実際は 「場合分け」 の方が 「確率」 より先で、場合分けがあって初めて確率が存在できるのである。
(「場合分けがあって初めて確率が存在できる」 というより 「場合分けができるような標本空間があって初めて確率が存在できる」 という方が正確である)
(場合分けをする前に考えている確率は数学の確率論の確率ではなく、日常の確率論の確率である)
モンティ・ホール問題や 3囚人問題の場合には、「事象」 と 「現象」 の区別が付いている場合と付いていない場合で次のような違いがおきる。
モンティ・ホール問題の場合なら、このようなメンタルモデルの違いにより次のような結果になる。
分かりやすく言うと、場合分けをして、それぞれの場合に確からしさを付与してから、問題を考えなければならない。
そして、モンティ・ホール問題や 3囚人問題を考えるときは、次のように場合分けをした上で確率を考えなければならない。
モンティ・ホール問題の場合は、どの扉が当りか、挑戦者はどの扉を選んだか、ホストはどの扉を開けたか、という観点を組み合わせて場合分けしなければならない。
3囚人問題の場合は、どの囚人が恩赦か、どの囚人が質問したか、看守はどの処刑囚人の名を上げたか、という観点を組合せて場合分けをしなければならない。
ところが、モンティ・ホール問題や3囚人問題の確率を錯覚する人たちは、このような多次元の空間で確率を考えないで、単に扉の配列や囚人の配列のような一次元の空間の上で確率を考えてしまう。
そのために確率を錯覚するのだ、というのが 「問題構造の把握失敗説」である。
Johnson-Laird, P. N., Legrenzi, P., Girotto, V., Legrenzi, M. S., & Caverni, J.-P. (1999). 、 Tubau, E. & Alonson, D. (2003). などが代表的な研究者である。
2014/10 に下記のように 「事象」 と 「現象」 の区別について補筆しました。
私は 「事象」 と 「現象」 の区別がついていないことがこのような 「問題構造の把握失敗」 の背景にあると思っている。
標本空間を素事象に分割し、確からしさを素事象に配分し、素事象を分類し、それぞれの分類に含まれる素事象の確からしさの総計を比較したものが確率であるという確率論の基本を教わる人は、理科系の学生でも少なそうである。 (2014年現在)
そのため、中学や高校で 「場合分け」 してから 「場合の数」 で確率を計算する方法を教わっただけの人たちは、 「場合分け」 が 「確率」 を計算する 手段だと誤解してしまうのだろう。
実際は 「場合分け」 の方が 「確率」 より先で、場合分けがあって初めて確率が存在できるのである。
(「場合分けがあって初めて確率が存在できる」 というより 「場合分けができるような標本空間があって初めて確率が存在できる」 という方が正確である)
(場合分けをする前に考えている確率は数学の確率論の確率ではなく、日常の確率論の確率である)
モンティ・ホール問題や 3囚人問題の場合には、「事象」 と 「現象」 の区別が付いている場合と付いていない場合で次のような違いがおきる。
| 現象 |
「事象」 と 「現象」 の 区別が付いている場合 |
「事象」 と 「現象」 の 区別が付いていない場合 |
|---|---|---|
|
現象1 賞品配置や処刑囚人が決まる |
賞品配置や処刑囚人によって場合分けする | 賞品配置や処刑囚人によって場合分けする |
| 確からしさを配分する |
確率を配分する |
|
| 配分された確率が 「事象」 ではなく賞品配置や処刑囚人といった 「現象」 に属すると勘違いする | ||
|
現象2 最初の扉や質問する囚人が決まる |
現象1と現象2を組み合わせて場合分けを細分化する | 現象2は現象1の確率に影響しないと考える |
|
それに合わせて確からしさを配分する |
||
|
現象3 選ばなかったハズレの扉が一つ開けられたり質問した囚人以外の処刑囚人の一人の名が明かされたりする |
上で細分化した場合分けに現象3 組み合わせてさらに細分化する | 現象3 が現象1の確率に直接影響すると勘違いする |
| それに合わせて確からしさを配分する |
問題構造の把握失敗 (不適切なメンタルモデル形成) |
|
|
確からしさを集計して確率を計算する |
不適切なメンタルモデルの上での確率計算 |
モンティ・ホール問題の場合なら、このようなメンタルモデルの違いにより次のような結果になる。
- 「事象」 と 「現象」 の区別が付いている人は、 「選んだ扉1 が当たりのときにハズレ扉3 が開けられた」 という 「事象」 の確からしさと、 「扉1 がハズレのときにハズレ扉3 が開けらた」 という 「事象」 の確からしさを比較する。 結果として確率の錯覚が起きにくい。
- 「事象」 と 「現象」 の区別が付いていない人、あるいはそもそも 「事象」 の概念の無い人は、 「ハズレ扉3 が開けれられた」 という 「現象」 が、 「選んだ扉1 が当たりかハズレか」 という 「現象」 の確率にどう影響するかを考える。 結果として確率の錯覚が生じやすい。
比率保存のヒューリスティク説
モンティ・ホール問題や3囚人問題の確率の錯覚の結果、どのような確率値が導かれるかというと、もともとの確からしさの比を保存するような値が導かれることが分っている。
例えば、モンティ・ホール問題の扉1、扉2、扉3が当りである確率がそれぞれ 0.2, 0.3, 0.5 の場合、ホストが扉3を開けた後の扉1と扉2が当りである確率の比がもともとの 0.2 : 0.3 の比を保持した値、つまり0.4 と 0.6 という確率が錯覚によって導かれる。
このような現象を無意識の思考、すなわちヒューリスティクによって説明するのが 「比率保存のヒューリスティク」 説である。
市川 伸一, 下條 信輔. (2010).が代表的な研究者であり、彼らはこのヒューリスティクを 「等比率の定理」 と呼んでいる。
類似の説に、扉の数や囚人の数を場合の数と考えて確率を計算するという 「場合の数ヒューリステlク」 (市川 伸一, 下條 信輔. (2010).は 「場合の数の定理」 と呼んでいる) というものもあるが、もともとの確からしさが均等でない場合の錯覚を説明できないので、あまり信憑性は高くない。
子供に比べて成人の方がモンティホール問題や3囚人問題に対して誤った解答をする人が多いことから、成長にともなって確率判断のヒューリスティクが形成されることがわかっている。
例えば、モンティ・ホール問題の扉1、扉2、扉3が当りである確率がそれぞれ 0.2, 0.3, 0.5 の場合、ホストが扉3を開けた後の扉1と扉2が当りである確率の比がもともとの 0.2 : 0.3 の比を保持した値、つまり0.4 と 0.6 という確率が錯覚によって導かれる。
このような現象を無意識の思考、すなわちヒューリスティクによって説明するのが 「比率保存のヒューリスティク」 説である。
市川 伸一, 下條 信輔. (2010).が代表的な研究者であり、彼らはこのヒューリスティクを 「等比率の定理」 と呼んでいる。
| 比率保存のヒューリスティク説 | |||||||||||||||||||||||||||||||||
ホストが扉を開ける前
ホストが扉3 を開けた後
|
看守が囚人の名を上げる前
看守が囚人B の名を上げた後
|
||||||||||||||||||||||||||||||||
類似の説に、扉の数や囚人の数を場合の数と考えて確率を計算するという 「場合の数ヒューリステlク」 (市川 伸一, 下條 信輔. (2010).は 「場合の数の定理」 と呼んでいる) というものもあるが、もともとの確からしさが均等でない場合の錯覚を説明できないので、あまり信憑性は高くない。
子供に比べて成人の方がモンティホール問題や3囚人問題に対して誤った解答をする人が多いことから、成長にともなって確率判断のヒューリスティクが形成されることがわかっている。
問題構造把握失敗の原因に関連する心理学研究
因果関係の把握の難しさに原因を求める説
Glymour, C.N. (2001). で、 モンティ・ホール問題ではホストが開ける扉という単1の結果に対して、互いに無関係な 2 つの原因、つまり当りの扉と挑戦者が選んだ扉の2 つの原因が関係しているというコライダー構造があるためにその2 つの原因の間の条件付依存関係 ( conditional dependence ) を把握するのが困難だと論じているらしい。
服部雅史, 西田豊, 他. (2009年ごろ). での、服部雅史先生の発表によると、
「モンティ・ホール問題が難しい理由は司会者がCのドアを開けたのは何故かという因果的な推論を大部分の解答者が行わないためではないか」
という説を確かめるために、
「司会者がCのドアを開けたのは、Bのドアのうしろに新車があるからではないか」という因果推定がなされやすいように変更したモンティ・ホール問題の問題文
で実験した結果、予測どおり正答率が上がったらしい。
寺尾敦・伊藤朋子 (2010). の結論部分で、3囚人問題で正しい問題表象を構成することは困難であり、特に難しいのは尤度の理解だろうと書いている。
【参考】尤度とは、仮説事象(確率を計算したい事象)を条件とする証拠事象(確率を計算する手がかりになる事象)の条件付き確率のことで、3囚人問題の場合で言えば、「囚人Aが恩赦のときに看守が囚人Bの名を上げる確率」などが尤度に当たる。
服部雅史, 西田豊, 他. (2009年ごろ). での、服部雅史先生の発表によると、
「モンティ・ホール問題が難しい理由は司会者がCのドアを開けたのは何故かという因果的な推論を大部分の解答者が行わないためではないか」
という説を確かめるために、
「司会者がCのドアを開けたのは、Bのドアのうしろに新車があるからではないか」という因果推定がなされやすいように変更したモンティ・ホール問題の問題文
で実験した結果、予測どおり正答率が上がったらしい。
寺尾敦・伊藤朋子 (2010). の結論部分で、3囚人問題で正しい問題表象を構成することは困難であり、特に難しいのは尤度の理解だろうと書いている。
【参考】尤度とは、仮説事象(確率を計算したい事象)を条件とする証拠事象(確率を計算する手がかりになる事象)の条件付き確率のことで、3囚人問題の場合で言えば、「囚人Aが恩赦のときに看守が囚人Bの名を上げる確率」などが尤度に当たる。
仮説事象と証拠事象の現象の類似性に原因を求める説
市川 伸一, 下條 信輔. (2010). に、 「3囚人問題ではデータ事象(Bが処刑されると看守が言ったこと)が原事象(Bが処刑されること)に直接関係しているので、「等比率の定理」などの主観的定理(ヒューリスティク)を適用した処理に誘導されやすい」という説が書かれている。
標本空間を分割した後は分割数を増やせない説
Fox, C.R. & Levav, J. (2004). で、人間が条件付き確率を計算するとき、 "Partition → Edit → Count"という手順を無意識にとるという説が提唱されている。Partition は 場合分けを行うことであり、Edit は起きなかった場合を刈り込むことであり、Count は条件付き確率を計算することである。
この仮説をモンティ・ホール問題に当てはめると、ひとたび当たり扉の場合分けを行った後ではホストが開ける扉も考慮した場合分けができなくなって「尤度の無視」 が起きるのだ、という風に確率の錯覚現象を説明できる。
モンティ・ホール問題の確率錯覚現象によく似た錯覚現象に二封筒問題の錯覚現象があり、二つの封筒を開ける前の二つの封筒の金額の大小関係の確率を、封筒を開けた後の中身の金額の大小関係の確率として考えてしまう現象であるが、モンティ・ホール問題とは次のような違いがある。
この仮説をモンティ・ホール問題に当てはめると、ひとたび当たり扉の場合分けを行った後ではホストが開ける扉も考慮した場合分けができなくなって「尤度の無視」 が起きるのだ、という風に確率の錯覚現象を説明できる。
モンティ・ホール問題の確率錯覚現象によく似た錯覚現象に二封筒問題の錯覚現象があり、二つの封筒を開ける前の二つの封筒の金額の大小関係の確率を、封筒を開けた後の中身の金額の大小関係の確率として考えてしまう現象であるが、モンティ・ホール問題とは次のような違いがある。
- モンティ・ホール問題の確率錯覚現象では扉に着目した確率が事後の扉に引き継がれる。
- 二封筒問題の確率錯覚現象では封筒に着目した確率が事後の「お金」に引き継がれる。
問題構造把握失敗の原因に関する私の説
私は、「問題構造の把握失敗」 の本質的な原因として
「客観確率幻想説」 というものを考えている。
これは、人間が確率を考えるとき、あたかもエネルギーや質量のように 保存される量として確率が宿ると考えている、 という説である。
さらにその結果としての 「課題空間取り違え説」 なるものを私は考えている。
扉という実体に確率が宿っていると考えているために、「標本空間」 の上で確率を考えずに、 扉が構成する 「扉空間」 の上で確率を考えてしまうという説である。
「扉空間」 の上で確率を考える人が、扉が一つ開かれたという知識をもとに扉の数を 3 から 2 に減らして、 その上で確率を考え続けようとする現象を 説明する原理として、「因果関逆転説」 というものも考えている。
「事後確率の問題を解くときに、通常の確率と同様に、証拠事象から仮説事象に向かう因果関係を探して、 それらしきものが見つかると、それにとびついて、単純な構造で確率を計算してしまうのだ」 という説である。
例えば、モンティ・ホール問題の場合、ホストが扉3 を開けたという証拠事象が、扉1が当たりである事象や、扉2 が当たりである 事象に与える因果関係を探し始めてしまい、そうしているうちに扉の数が 3 から 2 に減ったという現象を発見して、 それにすがって、2枚の扉で構成される空間の上で確率を考えてしまうのだろう。
そしてその結果として心理学者による 「問題構造の把握失敗説」 が述べるような錯覚した問題構造ができあがるのだろう。
私の 「因果関逆転説」 と、 心理学者による 「標本空間を分割した後は分割数を増やせない説」 は同じことを言っているのかも知れない。
以上をまとめると、次のような図式になる。 (黄緑の部分は私の説で、水色の部分は心理学者たちの説)
この図式をモンティ・ホール問題を例に図解すると次のようになる。
(この図では、モンティ・ホール問題で、挑戦者が選んだ扉を扉1 に限定した場合を例としています)
これは、人間が確率を考えるとき、あたかもエネルギーや質量のように 保存される量として確率が宿ると考えている、 という説である。
さらにその結果としての 「課題空間取り違え説」 なるものを私は考えている。
扉という実体に確率が宿っていると考えているために、「標本空間」 の上で確率を考えずに、 扉が構成する 「扉空間」 の上で確率を考えてしまうという説である。
「扉空間」 の上で確率を考える人が、扉が一つ開かれたという知識をもとに扉の数を 3 から 2 に減らして、 その上で確率を考え続けようとする現象を 説明する原理として、「因果関逆転説」 というものも考えている。
「事後確率の問題を解くときに、通常の確率と同様に、証拠事象から仮説事象に向かう因果関係を探して、 それらしきものが見つかると、それにとびついて、単純な構造で確率を計算してしまうのだ」 という説である。
例えば、モンティ・ホール問題の場合、ホストが扉3 を開けたという証拠事象が、扉1が当たりである事象や、扉2 が当たりである 事象に与える因果関係を探し始めてしまい、そうしているうちに扉の数が 3 から 2 に減ったという現象を発見して、 それにすがって、2枚の扉で構成される空間の上で確率を考えてしまうのだろう。
そしてその結果として心理学者による 「問題構造の把握失敗説」 が述べるような錯覚した問題構造ができあがるのだろう。
私の 「因果関逆転説」 と、 心理学者による 「標本空間を分割した後は分割数を増やせない説」 は同じことを言っているのかも知れない。
以上をまとめると、次のような図式になる。 (黄緑の部分は私の説で、水色の部分は心理学者たちの説)
|
客観確率幻想
(扉自体に確率が宿ると考える) |
| ↓ |
|
(扉によって構成される空間の上で確率を考えてしまう) |
|
↓
どの扉が開けられたか知らされる ↓ |
|
(ホストが扉を開けたことが当たり扉に与える影響を探し始める) |
| あるいは |
|
(証拠事象に反する仮説事象を刈り込む) |
| ↓ |
|
|
| あるいは |
|
|
| ↓ |
|
当り扉の空間から 扉を減らしただけの 一次元の空間の上で確率を考えてしまう |
| ↓ |
|
|
| ↓ |
|
|
この図式をモンティ・ホール問題を例に図解すると次のようになる。
(この図では、モンティ・ホール問題で、挑戦者が選んだ扉を扉1 に限定した場合を例としています)
|
最初の扉空間 (扉自体の空間)
ホストがどの扉を開けたかの情報
ホストが開けた扉の情報が 扉空間に 作用すると考える ↓ ホストが扉を開けた 後の扉空間 (扉3 欠如)
確率の比率を保存しながら 事後の確率を計算する
|
標本空間で考える人の頭の中
どの扉が当りかの事象の空間
ホストがどの扉を開けたかの事象の空間
標本空間の分割 (場合分け) を行う ↓ 標本空間からホストが扉3 を 開けた後の部分を切り出す
確率の比率を保存しながら 事後の確率を計算する
|
確率を錯覚する理由について、「第ニ部 モンティ・ホール問題と3囚人問題の認知心理学的検討」や、「第三部 心理学者によるモンティ・ホール問題と3囚人問題の研究 」でさらに詳しく調べています。
解くことが難しい理由の手っ取り早い説明
モンティ・ホール問題や3囚人問題が数学者も間違える有名な問題ならば自分で解いてやろうと挑戦してもそう簡単には解けない。その理由を、私は次のように考える。
正解の方こそ間違っているという疑いを晴らすのは容易でない
日常の確率概念では 「確率を錯覚する理由の手っ取り早い説明」 で述べたような 「客観確率幻想」 に基づいて確率を計算して、
数学の確率概念では、 「標本空間」 に基づいて確率を計算している。
ところがその違いがはっきりするような経験が乏しいために、日常の確率概念と数学の確率が概念で確率が異なることがあることを知っている人は稀である。
このような下地の上に、「自分は数学が得意である」という自負を持っている人が数学が得意でなさそうな人にモンティ・ホール問題や 3囚人問題の正解を示されても、自分が出した答えが錯覚である可能性に気付かず、 詳細な場合分けを行って確かめようという気が起きないのだろう。
数学の確率概念では、 「標本空間」 に基づいて確率を計算している。
ところがその違いがはっきりするような経験が乏しいために、日常の確率概念と数学の確率が概念で確率が異なることがあることを知っている人は稀である。
このような下地の上に、「自分は数学が得意である」という自負を持っている人が数学が得意でなさそうな人にモンティ・ホール問題や 3囚人問題の正解を示されても、自分が出した答えが錯覚である可能性に気付かず、 詳細な場合分けを行って確かめようという気が起きないのだろう。
「条件付確率」 の概念を知らない
モンティ・ホール問題の場合、ホストが これこれの 扉を開けた時点の確率を求める問題ととらえることが多い。
3囚人問題の場合、看守が処刑される だれそれの 囚人の名を上げた時点での確率を求める問題ととらえることが多い。
このような問題のとらえ方をした場合には、これこれの扉が開けられたという条件や、 これこれの囚人の名が上がったという条件の下での「条件付確率」 を計算しなければならないが、「条件付き確率」 の概念さえあれば、 手間と時間が掛かって苦労するかも知れないが、正解を出すのは難しくない。
ところが、3囚人問題はともかく、モンティ・ホール問題は一般の人にも知られる有名な問題であるため、「条件付き確率」の概念になじみの薄い人まで関心を持ってしまって、立ち往生するのだろう。
3囚人問題の場合、看守が処刑される だれそれの 囚人の名を上げた時点での確率を求める問題ととらえることが多い。
このような問題のとらえ方をした場合には、これこれの扉が開けられたという条件や、 これこれの囚人の名が上がったという条件の下での「条件付確率」 を計算しなければならないが、「条件付き確率」 の概念さえあれば、 手間と時間が掛かって苦労するかも知れないが、正解を出すのは難しくない。
ところが、3囚人問題はともかく、モンティ・ホール問題は一般の人にも知られる有名な問題であるため、「条件付き確率」の概念になじみの薄い人まで関心を持ってしまって、立ち往生するのだろう。
「事後確率」 や 「原因の確率」 、すなわち 「因果関係の逆転した条件付確率」 の教育を受けていない
ホストが開けた扉を特定したり、看守が名を上げた囚人を特定した問題のとらえ方をした場合には、確率を計算する対象の事象 (仮説事象) から、確率を計算するヒントになる事象 (証拠事象) に向けた因果関係が成立する。
確率論ではこのような因果関係がある場合、 証拠事象の下での仮説事象の確率を単に 「条件付き確率」 と呼ぶ代わりに 「事後確率」 あるいは 「原因の確率」 と呼んでいる。
ところが、 「事後確率」 や 「原因の確率」 の計算方法を学校で習うことは稀なので、私のようにせいぜい 「条件付確率」 の知識しかない人は苦労することになる。現に私も、モンティ・ホール問題を解こうという気が起きたその日のうちに正解にたどり着くことができなかった。
インターネットでのQAを読むと、2010年代になっても、高校で教えていないらしいことがわかる。
| 問題 |
確率を計算する対象の事象 (仮説事象) |
因果 関係 |
確率を計算する ヒントになる事象 (証拠事象) |
|---|---|---|---|
| モンティ・ホール問題 | 挑戦者が選んだ扉とホストが開け残した扉の当たりハズレ | → | ホストがこれこれの扉を開けた |
| 3囚人問題 | 質問した囚人と看守が名を上げなかった囚人の恩赦か否か | → | 看守がこれこれの囚人の名を上げた |
確率論ではこのような因果関係がある場合、 証拠事象の下での仮説事象の確率を単に 「条件付き確率」 と呼ぶ代わりに 「事後確率」 あるいは 「原因の確率」 と呼んでいる。
ところが、 「事後確率」 や 「原因の確率」 の計算方法を学校で習うことは稀なので、私のようにせいぜい 「条件付確率」 の知識しかない人は苦労することになる。現に私も、モンティ・ホール問題を解こうという気が起きたその日のうちに正解にたどり着くことができなかった。
インターネットでのQAを読むと、2010年代になっても、高校で教えていないらしいことがわかる。
尤度が問題文に書かれておらず、解く者が自力で導かねばならない
確率を計算する者が尤度を自力で導かなければならないところが、モンティ・ホール問題や3囚人問題と、マンモグラフィー検査など他の確率錯覚現象との大きな違いの一つである。
※ 尤度 とは仮説事象が成立した場合に証拠事象が成立する確率であり、次のようになっている。
( この表では、モンティ・ホール問題では挑戦者が扉1 を選びホストが扉3 を開けた場合に限定し、 3囚人問題では囚人A が質問して、看守が囚人B が処刑さと答えた場合に限定 )
※ 尤度 とは仮説事象が成立した場合に証拠事象が成立する確率であり、次のようになっている。
( この表では、モンティ・ホール問題では挑戦者が扉1 を選びホストが扉3 を開けた場合に限定し、 3囚人問題では囚人A が質問して、看守が囚人B が処刑さと答えた場合に限定 )
| 問題 | 仮説事象 | 証拠事象 | 尤度の明示 |
|---|---|---|---|
| モンティ・ホール問題 | 扉1が当り | ホストが扉3を開けた | なし |
| 扉2が当り | なし | ||
| 3囚人問題 | 囚人Aが恩赦 | 看守が囚人Bが処刑されると答えた | なし |
|
|
なし | ||
| マンモグラフィー検査 | 乳癌がある | マンモグラフィー検査で陽性 | あり |
| 乳癌がない | あり |
ホストや看守の行動が「織り込み済み」であることに気付くことは容易でない
モンティ・ホール問題や3囚人問題を素人向けに説明する場合、「ホストがいずれかのハズレ扉を開けることや、看守がいずれかの処刑囚人の名を上げることが最初から決まっているのだから確率は変わらない」と説明することがある。
そうした説明は,、後述する不特定事象による条件付確率あるいは事後確率の問題設定 をとった場合には全く正しいが、私を含む普通の人には思いつきにくい。
例えば、モンティ・ホール問題であれば、「ホストがハズレ扉の中から扉3を選んで開けた」という文を、「ホストがいずれかのハズレ扉を開けた」と読み変えなければならない。しかし、「扉3が開いている」という情景を思い浮かべながら、「扉2と扉3のいずれかが開いている」と読み替えることは困難である。
私も、こうした読み替えが理解できなかったために苦労した一人である。
そうした説明は,、後述する不特定事象による条件付確率あるいは事後確率の問題設定 をとった場合には全く正しいが、私を含む普通の人には思いつきにくい。
例えば、モンティ・ホール問題であれば、「ホストがハズレ扉の中から扉3を選んで開けた」という文を、「ホストがいずれかのハズレ扉を開けた」と読み変えなければならない。しかし、「扉3が開いている」という情景を思い浮かべながら、「扉2と扉3のいずれかが開いている」と読み替えることは困難である。
私も、こうした読み替えが理解できなかったために苦労した一人である。
解き方の手っ取り早い説明
モンティ・ホール問題を例に説明する。(3囚人問題の場合も同様に説明することができる)
挑戦者が選んだ扉とホストが開けた扉を特定して「条件付確率」あるいは「事後確率」を計算する場合
(2016/08/21に説明文を訂正しました。)
挑戦者がどれか特定の扉を選び、ホストが残りの扉のうちハズレの扉のどれか特定の扉を開けた時点について考える。
挑戦者が選んだ扉が当たりである場合、ホストが開けなかった方の扉についても、開ける可能性があった。
挑戦者がハズレを選んだ場合、ホストが開けた扉以外にホストは開けることができなかった。
従って、ホストがどれか特定のの扉を開けたとき次のようになる。
挑戦者が選んだ扉が当たりであるという事象の余事象、つまり挑戦者が選んだ扉がハズレであるという事象を考慮すると、次のようなもっと簡単な計算ができる。
ホストが扉を開ける前には、「挑戦者が選んだ扉が当たりである」 可能性と 「挑戦者が選んだ扉がハズレである」 可能性は 1対2 であった。
ホストがどれか特定のの扉を開けたとき次のようになる。
挑戦者がどれか特定の扉を選び、ホストが残りの扉のうちハズレの扉のどれか特定の扉を開けた時点について考える。
挑戦者が選んだ扉が当たりである場合、ホストが開けなかった方の扉についても、開ける可能性があった。
挑戦者がハズレを選んだ場合、ホストが開けた扉以外にホストは開けることができなかった。
従って、ホストがどれか特定のの扉を開けたとき次のようになる。
「挑戦者が選んだ特定の扉が当たりである」 可能性は半分になった。
「挑戦者が選ばなかった中からホストが開け残した特定の扉が当たりである」 可能性は半分にならなかった。
従って、挑戦者が選んだ特定の扉と、ホストが開け残した特定の扉に賞品がある可能性の比が 1対2 となり、確率はそれぞれ 1/3 と 2/3 になる。
「挑戦者が選ばなかった中からホストが開け残した特定の扉が当たりである」 可能性は半分にならなかった。
挑戦者が選んだ扉が当たりであるという事象の余事象、つまり挑戦者が選んだ扉がハズレであるという事象を考慮すると、次のようなもっと簡単な計算ができる。
ホストが扉を開ける前には、「挑戦者が選んだ扉が当たりである」 可能性と 「挑戦者が選んだ扉がハズレである」 可能性は 1対2 であった。
ホストがどれか特定のの扉を開けたとき次のようになる。
「挑戦者が選んだ扉が当たりである」 可能性が半分になった。(ホストが別の扉を開ける可能性がなくなったため)
「挑戦者が選んだ扉がハズレである」 可能性も半分になった。(開けられた扉の分が消えたため)
従って、「挑戦者が選んだ扉が当たりである」 可能性と 「挑戦者が選んだ扉がハズレである」 可能性の比が 1対2 のままで変化せず、確率はそれぞれ 1/3 と 2/3 になる。
「挑戦者が選んだ扉がハズレである」 可能性も半分になった。(開けられた扉の分が消えたため)
挑戦者が扉1を選び、ホストが扉3を開けた場合の説明図
ホストがどの扉を開けたか特定しないで、「条件付確率」あるいは「事後確率」を計算する場合
(2016/08/21に説明文を訂正しました。)
簡単のため、挑戦者が扉1を選んだ場合を考える。
挑戦者が選んだ扉1が当たりの場合、選ばなかった扉2が当たりの場合、そして扉3が当たりの場合すべてに平等に、「ホストが挑戦者が選ばなかったハズレ扉の一つを開ける」という結果がもたらされる。
従って、ホストが挑戦者が選ばなかったハズレ扉の一つを開けた後、それぞれの扉が当たりである可能性は等しいままである。
従って、挑戦者が選んだ特定の扉 (一つの扉) と、挑戦者が選ばなかった中からホストが開け残した不特定の扉 (二つの扉) に賞品がある可能性の比が 1対2 となり、確率はそれぞれ 1/3 と 2/3 になる。
ここで注意しなければならないのは、ここで求めた 2/3 はホストが開け残した扉を特定して計算した確率ではなく、あくまでも、ホストが開け残した扉がどれであるかを区別しないで計算した確率だということである。
簡単のため、挑戦者が扉1を選んだ場合を考える。
挑戦者が選んだ扉1が当たりの場合、選ばなかった扉2が当たりの場合、そして扉3が当たりの場合すべてに平等に、「ホストが挑戦者が選ばなかったハズレ扉の一つを開ける」という結果がもたらされる。
従って、ホストが挑戦者が選ばなかったハズレ扉の一つを開けた後、それぞれの扉が当たりである可能性は等しいままである。
従って、挑戦者が選んだ特定の扉 (一つの扉) と、挑戦者が選ばなかった中からホストが開け残した不特定の扉 (二つの扉) に賞品がある可能性の比が 1対2 となり、確率はそれぞれ 1/3 と 2/3 になる。
ここで注意しなければならないのは、ここで求めた 2/3 はホストが開け残した扉を特定して計算した確率ではなく、あくまでも、ホストが開け残した扉がどれであるかを区別しないで計算した確率だということである。
挑戦者が扉1を選んだ場合の説明図
ホストが挑戦者が選ばなかった残りの中のハズレの扉を開けることは最初から分っているとして「非条件付確率」を計算する場合
挑戦者が選んだ扉が当たりであれば、選ばなかった扉のうちホストが開け残した扉はハズレであり、逆も真である。
挑戦者が選んだ扉がハズレであれば、選ばなかった扉のうちホストが開け残した扉は当たりであり、逆も真である。
挑戦者が選んだ扉が当たりである確率とハズレである確率がそれぞれ 1/3 と 2/3 であるので、挑戦者が選んだ扉と、選ばなかった扉のうちホストが開け残した扉に賞品がある確率は、それぞれ 1/3 と 2/3 となる。
挑戦者が選んだ扉がハズレであれば、選ばなかった扉のうちホストが開け残した扉は当たりであり、逆も真である。
挑戦者が選んだ扉が当たりである確率とハズレである確率がそれぞれ 1/3 と 2/3 であるので、挑戦者が選んだ扉と、選ばなかった扉のうちホストが開け残した扉に賞品がある確率は、それぞれ 1/3 と 2/3 となる。
挑戦者が扉1を選んだ場合の説明図
数学者の目で見ると、上記のそれぞれの計算方法は確率を付与する事象のとらえ方という本質的な部分が異なるので、まったく別の問題を解いていることになる。 そのことは統計データを処理するときの集計方法が異なることからわかる。
| 計算方法 | 統計データの集計方法の違い |
|---|---|
| 挑戦者が選んだ扉とホストが開けた扉を特定して「条件付確率」あるいは「事後確率」を計算する場合 | 統計データを集計するとき、ホストが開けた扉ごとに別々に集計する。 |
| ホストがどの扉を開けたか特定しないで、「条件付確率」あるいは「事後確率」を計算する場合 |
統計データを集計するとき、ホストが開けた扉を区別しないで集計する。 ホストが扉を開けないことがありうるような条件でも、計算ができる。 |
| ホストが挑戦者が選ばなかった残りの中のハズレの扉を開けることは最初から分っているとして「非条件付確率」を計算する場合 |
統計データを集計するとき、ホストが開けた扉を区別しないで集計する。 ホストが扉を開けないことがありうるような条件では、計算が成り立たない。 |
このような違いがあっても計算結果が等しくなるのは、モンティ・ホール問題で言えば、当たり扉の選定とホストが開ける扉の選定の両面で3つの扉の間に対称性があることに起因し、3囚人問題で言えば、恩赦になる囚人の選定と看守が名を上げる囚人の選定の両面で3人の囚人の間に対称性があることに起因している。
モンティ・ホール問題に詳しいと自認している人たちでも、これら3つのとらえ方があることを理解している人は非常に少なくて、Wikipedia(英語版)の"Monty Hall problem"の記事(2012年3月19日20:49版)の"Criticism of the simple solutions"の項でも、とらえ方①とその他を区別しているが、とらえ方②と③は区別していない。(ホストが必ず扉を開けてくれるなら、とらえ方の②と③は区別しても意味が無いので、気付いていて省略しているのかも知れない)
補足
上の「挑戦者が選んだ扉とホストが開けた扉を特定して「条件付確率」あるいは「事後確率」を計算する場合」の説明では、挑戦者が選んだ扉1が当たりのときにホストが開ける扉に「くせ」や「偏り」がないことを前提にしている。 しかし、「くせも偏りもない人はいない」と考える人もいるので、そういう人のための説明図も用意した。この図が示すように、挑戦者が選んだ扉1が当たりのときにホストが開ける扉に「くせ」」がある場合には、ホストが扉3を開けて開け残した扉2に賞品がある確率は 1と 1/2 の間の数値になる。
モンティ・ホール問題の問題文に曖昧さがあるので、扉を変えて賞品を得る確率が 2/3 だとする標準的な解答だけでは不完全だとする議論を「ワーディングの議論」と呼ぶ。そしてそのような議論を好む人たちが、ここで上げたようなホストの行動パターンを論じることがよくある。
正統的な問題の捉え方はどれかの手っ取り早い説明
モンティ・ホール問題の元祖を基準とした場合
American Statiscian の1975年2月号に載った問題文 (Selvin, Steve (1975a).) がモンティ・ホール問題の元祖であり、著者の Steve Selvin は「非条件付確率の問題設定(挑戦者が選ぶ扉を限定しない方法)」による答えを添えていた。
このことから、次のような考え方があり得る。
このことから、次のような考え方があり得る。
「非条件付確率」を計算する」 解き方がモンティ・ホール問題の問題文の元祖に付随していたのであるから、これが正統的な解き方である。
自然な解き方を基準とした場合
3囚人問題では看守から情報が与えられることにより状況が変化し、モンティ・ホール問題で扉が一つ開けられることにより、状況が変化している。このような場合、状況の変化を踏まえて確率を再計算するのが人間の常であるから、これらが難問だと知った上で、あるいは 「確率1/2 は間違いらしい」 と知った上で解き始める場合、きちんと場合分けを行うことにより 「条件付確率」 を計算しようとするものである。
現に私がモンティ・ホール問題に初めて接したときには次のような手順で手間暇かけて解いたものである。
現に私がモンティ・ホール問題に初めて接したときには次のような手順で手間暇かけて解いたものである。
- 「賞品を隠す」、「挑戦者が扉を選ぶ」、「モンティ・ホールが扉を開ける」という現象の順番にそって場合を分けて行く。
- それぞれの段階で確率を割り振っておいて、それを分割することにより次の段階の確率を求める。
人間の習性から考えて、「挑戦者が選んだ扉とホストが開けた扉を特定して条件付確率を計算する」 解き方が自然であるから、これが正統的な解き方である。
問題の捉え方によって答えが違ってもおかしくないことの手っ取り早い説明
モンティ・ホール問題を例に説明する。(3囚人問題の場合も同様に説明することができる)
モンティ・ホール問題のホストの行動に癖があると、
「挑戦者が選んだ扉とホストが開けた扉を特定して計算する場合」と
「ホストがどの扉を開けたか特定せず計算する場合」とで
答えが一致しない場合が生じる。
例えば、挑戦者が当たりを選んだときにホストが開ける扉に好みがあると、
「挑戦者が選んだ扉とホストが開けた扉を特定して計算する場合」は、switchして賞品を得る確率が 2/3 にならないが、
「ホストがどの扉を開けたか特定せず計算する場合」には、普通と変わらずに、2/3 である。
この事態に矛盾を感じる人もいるようである。例えば次のような例がある。
モンティ・ホール問題のホストの行動に癖があると、
「挑戦者が選んだ扉とホストが開けた扉を特定して計算する場合」と
「ホストがどの扉を開けたか特定せず計算する場合」とで
答えが一致しない場合が生じる。
例えば、挑戦者が当たりを選んだときにホストが開ける扉に好みがあると、
「挑戦者が選んだ扉とホストが開けた扉を特定して計算する場合」は、switchして賞品を得る確率が 2/3 にならないが、
「ホストがどの扉を開けたか特定せず計算する場合」には、普通と変わらずに、2/3 である。
この事態に矛盾を感じる人もいるようである。例えば次のような例がある。
Yahoo!知恵袋の例 モンティ・ホール問題でベイズの定理を使うと矛盾が起こる気がするのですが・・・.
この疑問に対して、次のような2段階の説明で答えることができる。
第1段:統計データから確率を計算することを想像すると、確率が食い違う理由がよくわかる。
「挑戦者が選んだ扉とホストが開けた扉を特定して計算する場合」、例えば挑戦者が扉1を選び、ホストが扉3を開けたというケースについて確率を計算する場合には、ホストが扉3を開けたというデータを使うが、ホストが扉2を開けたというデータは使わずに確率を計算することになる。
他方、「ホストがどの扉を開けたか特定せず計算する場合」、例えば、挑戦者が扉1を選び、ホストが残りのどちらかを開けたというケースについて計算する場合には、ホストが扉3を開けたデータと、扉2を開けたデータの両方を使って計算することになる。
このような違いがあるため、挑戦者が当たりを選んだときにホストが開ける扉に癖があると、計算結果が食い違ってくる。
他方、「ホストがどの扉を開けたか特定せず計算する場合」、例えば、挑戦者が扉1を選び、ホストが残りのどちらかを開けたというケースについて計算する場合には、ホストが扉3を開けたデータと、扉2を開けたデータの両方を使って計算することになる。
このような違いがあるため、挑戦者が当たりを選んだときにホストが開ける扉に癖があると、計算結果が食い違ってくる。
第2段:確率の本質が 「予想」 あるいは 「頻度」 であることに気付けば、異なる確率値が並存することが不思議でなくなる。
そもそも確率論とは、数学のできるギャンブラー:カルダーノと、ギャンブルのできる数学者:パスカルが創りだした理論であって、出発点は博打の理論である。そして二人とも「標本空間」の分析に力点を置いていた。このことから「確率」の本質が「標本空間」の認識に基づく 「予想」 あるいは 「頻度」 であることがわかる。
注:ある特定のゲームについて考える確率が「予想」で、何回かゲームを行った場合のトータルで考える確率が「頻度」である。
この考えに基づけば、モンティ・ホール問題で確率の食い違いが発生しても不思議でなくなる。
ホストの癖を知っている予想屋は 「挑戦者が選んだ扉とホストが開けた扉を区別できるような標本空間で【頻度】を計算して【予想】する」 だろうし、そうでない予想屋は 「ホストがどの扉を開けたかを区別できないような標本空間で【頻度】を計算して【予想】する」 だろうから、計算結果の確率が異なって当然である。
ホストの癖を知っている予想屋は 「挑戦者が選んだ扉とホストが開けた扉を区別できるような標本空間で【頻度】を計算して【予想】する」 だろうし、そうでない予想屋は 「ホストがどの扉を開けたかを区別できないような標本空間で【頻度】を計算して【予想】する」 だろうから、計算結果の確率が異なって当然である。
不思議さの手っ取り早い説明
モンティ・ホール問題で switch して賞品を得る確率が 2 / 3 だったり、質問しなかった方の囚人が恩赦になる確率が 2 / 3 になる理由を教わって頭で理解しても心で納得できる人はいない。(世界に何人かいるかも知れないが私は聞いたことがない)
そして、心で納得するために分りやすい説明を探しあぐねてモンティ・ホール問題にはまる人が多い。私もその一人だ。
心理学者たちはこのような心の働きの原因を、無意識の確率思考方法、すなわち確率判断のヒューリスティクに求めている。
これに対して、私は、「確率を錯覚する理由の手っ取り早い説明」 の項で述べたような「客観確率幻想」と、それに由来する「課題空間の取り違え」が不思議さの原因だろうと、考えている。
「事象」 が持つ 「確からしさ」 が 「全事象」 の確からしさの総計の中に占める 「率」 が 「確率」 であるという意識が徹底していないために、「扉」や「囚人」という具体的な 「現象」 や 「事物」 が持つエネルギーか何かのような 「量」 が 「確率」 だと勘違いしているのである。(客観確率幻想)
モンティ・ホール問題であれば、「扉1が当たりで挑戦者が扉1を選びホストが扉3を選ぶ事象の確からしさ」 と 「扉2が当たりで挑戦者が扉1を選びホストが扉3を選ぶ事象の確からしさ」 を比較するのでなく、ホストが扉3を開けた後に 「扉1が持つ確率」 と 「扉2が持つ確率」 をホストが扉3を開ける前の確率から直接に計算してしまうのである。
3囚人問題であれば、「囚人Aが恩赦で囚人Aが質問し看守が囚人Bの名を上げる事象の確からしさ」 と 「囚人Cが恩赦で囚人Aが質問し看守が囚人Bの名を上げる事象の確からしさ」 を比較するのでなく、看守が囚人Bの名を上げた後に 「囚人Aが持つ確率」 と 「囚人Cが持つ確率」 を看守が囚人Bの名を上げる前の確率から直接に計算してしまうのである。
このような客観確率幻想に陥って課題空間を取り違えている人の頭の中では、下の図のように不思議さを感じているのだろうと、私自身の体験から考えている。
そして、心で納得するために分りやすい説明を探しあぐねてモンティ・ホール問題にはまる人が多い。私もその一人だ。
心理学者たちはこのような心の働きの原因を、無意識の確率思考方法、すなわち確率判断のヒューリスティクに求めている。
これに対して、私は、「確率を錯覚する理由の手っ取り早い説明」 の項で述べたような「客観確率幻想」と、それに由来する「課題空間の取り違え」が不思議さの原因だろうと、考えている。
「事象」 が持つ 「確からしさ」 が 「全事象」 の確からしさの総計の中に占める 「率」 が 「確率」 であるという意識が徹底していないために、「扉」や「囚人」という具体的な 「現象」 や 「事物」 が持つエネルギーか何かのような 「量」 が 「確率」 だと勘違いしているのである。(客観確率幻想)
モンティ・ホール問題であれば、「扉1が当たりで挑戦者が扉1を選びホストが扉3を選ぶ事象の確からしさ」 と 「扉2が当たりで挑戦者が扉1を選びホストが扉3を選ぶ事象の確からしさ」 を比較するのでなく、ホストが扉3を開けた後に 「扉1が持つ確率」 と 「扉2が持つ確率」 をホストが扉3を開ける前の確率から直接に計算してしまうのである。
3囚人問題であれば、「囚人Aが恩赦で囚人Aが質問し看守が囚人Bの名を上げる事象の確からしさ」 と 「囚人Cが恩赦で囚人Aが質問し看守が囚人Bの名を上げる事象の確からしさ」 を比較するのでなく、看守が囚人Bの名を上げた後に 「囚人Aが持つ確率」 と 「囚人Cが持つ確率」 を看守が囚人Bの名を上げる前の確率から直接に計算してしまうのである。
このような客観確率幻想に陥って課題空間を取り違えている人の頭の中では、下の図のように不思議さを感じているのだろうと、私自身の体験から考えている。
最初の扉空間
ホストが開ける扉空間
客観確率幻想 ↓ ホストが扉3を開けた 後の扉空間
|
最初の囚人空間
看守が名を上げる囚人空間
客観確率幻想 ↓ 看守が囚人Bの名を 上げた後の囚人空間
|
不思議さを払拭するには時間を掛けるしか方法が無い
モンティ・ホール問題や3囚人問題の不思議さは無意識の錯覚心理によるものなので、自分なりに説明を考えたり、色々な説明を読んだりしても不思議さはなくならない。
不思議さを払拭するには、これらと長くつきあって、無意識のヒューリスティクや直感的な確率概念の働きを徐々に弱めるしかない。
このことは私の実体験に基づいているので、間違いない。
不思議さを払拭するには、これらと長くつきあって、無意識のヒューリスティクや直感的な確率概念の働きを徐々に弱めるしかない。
このことは私の実体験に基づいているので、間違いない。
不思議さが薄まっても気味の悪さが残るわけ
私の体験では、モンティ・ホール問題と長年付き合った結果不思議さが薄れた代わりに気味の悪さを強く感じ始め、数年間そうしたことが続いた。
こうしたことから私は確率の認知メカニズムの中に 「日常的確率論」 より原始的な 「本能的確率論」 のレベルがあるという説を思いついた。
「3囚人問題やモンティ・ホール問題の答えを理解して日常的確率論の働きが止まって不思議さが薄まっても、本能的確率論の働きが止まらないために気味の悪さを感じるのだ」 と説明できそうである。
こうしたことから私は確率の認知メカニズムの中に 「日常的確率論」 より原始的な 「本能的確率論」 のレベルがあるという説を思いついた。
| 確率論のレベル | 特徴 |
|---|---|
| 数学的確率論 | 状況の変化が起きた場合、最初に行った場合分けに状況の変化を組み合わせて細分化する。 |
| 日常的確率論 | 最初に行った場合分けで計算した確率をエネルギーか何かのように錯覚しているため、状況の変化を組み合わせて場合分けを細分化することができない。 |
| 本能的確率論 |
確率の対象になる現象がこれから発生する現象のように錯覚する。 (3囚人問題であれば看守が一人の処刑囚人の名を上げた後に恩赦囚人が決まるように錯覚し、モンティ・ホール問題であれば、扉が開けられた後に賞品の扉が決まるように錯覚する) |
「3囚人問題やモンティ・ホール問題の答えを理解して日常的確率論の働きが止まって不思議さが薄まっても、本能的確率論の働きが止まらないために気味の悪さを感じるのだ」 と説明できそうである。
数学の問題としてのとらえ方
確率の問題としてモンティ・ホール問題や3囚人問題をとらえるとらえ方は何を確率変数ととらえ、 標本空間の範囲をどうとらえ、 何を仮説事象ととらえ、 何を証拠事象ととらえるかで分類できる。
これらの分類のそれぞれについて、挑戦者が選ぶ扉がどれか、あるいは看守に質問したのは誰か、などの中間事象を限定して考えるか、限定せずに考えるかで、さらに細分化することができる。
さらに中間事象を限定する場合の解法を次の2種類に分類できる。
これらの分類のそれぞれについて、挑戦者が選ぶ扉がどれか、あるいは看守に質問したのは誰か、などの中間事象を限定して考えるか、限定せずに考えるかで、さらに細分化することができる。
さらに中間事象を限定する場合の解法を次の2種類に分類できる。
※ 後述の 「問題の解法の変わり種」 で述べるように、 中間事象 を限定する代わりに当り扉や恩赦囚人などの 初期事象 を限定する方法もあるが、煩雑になるので割愛する。
以下、数学の問題としてのとらえ方を分類するに当って、確率変数のとらえ方は次のような標準的なとらえ方に限定することとする。
以下、数学の問題としてのとらえ方を分類するに当って、確率変数のとらえ方は次のような標準的なとらえ方に限定することとする。
- ◇賞品の配置や恩赦になる囚人に関する確率変数の値域は
{ 扉1, 扉2, 扉3 } や、{ 囚人 A, 囚B, 囚人C } とする。 - ◇挑戦者が選んだ扉や看守に質問した囚人を表す確率変数の値域は、それぞれ
{ 扉1, 扉2, 扉3 } もしくは、{ 囚人A, 囚人B, 囚人C } とする。 - ◇ホストが開けた扉や看守が名を上げた囚人を表す確率変数の値域は、それぞれ
{ 扉1, 扉2, 扉3, 何も開けない } もしくは、{ 囚人A, 囚人B, 囚人C, 誰の名も上げない } とする。
ホストが扉を開けなかったり、看守が答えなかったりするケースも含む場合の確率変数の立て方には次の2種類がある。
- ①ホストが扉を開けるか否かを表したり、看守が答えてくれるか否かを表す別個の確率変数を立てる方法
- ②ホストがあけた扉や看守が名を上げた囚人を表す確率変数の値域に、ホストが開けないケースや看守が答えないケースも含める方法
参考 2 :
賞品や恩赦の配置に関する確率変数については、ハズレ賞品である2頭のヤギを区別したり、 恩赦にならない囚人の処刑方法を区別するやり方もあるが、 煩雑になるので割愛する。
結果として、数学の問題としてのとらえ方は、下のように分類することができる。
凡例: [M]:モンティ・ホール問題 [3]:3囚人問題
| 問題設定のニックネーム | 標本空間の範囲 | 仮説事象 | 中間事象の限定 | 解法の分類 | 証拠事象 | 代表的な論者または文献 |
|---|---|---|---|---|---|---|
| 特定事象による条件付確率あるいは事後確率の問題設定 |
[M] ホストが扉を開けないケースやホストが挑戦者が選んだ扉を開けてしまうケースも範囲に含む。 [3] 看守が答えないケースや看守が質問した囚人の運命を告げるケースも範囲に含む |
[M] 扉1があたり、扉2が当たり、および扉3が当たりのそれぞれの事象 [3] 囚人Aが恩赦、囚人Bが恩赦、および囚人Cが恩赦のそれぞれの事象 |
中間事象の限定なし | 中間事象を証拠事象の一部として計算する解法 |
[M] 挑戦者が扉A を選び、ホストがハズレ扉B (A以外) を開けた [3] 囚人X が看守に質問し、看守が囚人Y (X以外) が処刑されると明かした |
Wikipedia(英語版)の"Monty Hall Probrem"の記事の"Baye's Theorem"の項 (2011年09月05日版) |
|
[M] 挑戦者が選んだ扉を特定 [3] 看守に質問した囚人を特定 |
中間事象を証拠事象の一部として計算する解法 |
[M] 挑戦者がこれこれの扉を選び、ホストがこれこれのハズレ扉 (挑戦者が選んだ扉以外) を開けた [3] 囚人だれそれが看守に質問し、看守がだれそれ (質問した囚人以外) が処刑されると明かした |
Selvin, Steve (1975b). | |||
| 中間事象で切り取られた範囲に標本空間を限定して計算する解法 |
[M] ホストがこれこれのハズレ扉 (挑戦者が選んだ扉以外) を開けた [3] 質問した囚人に看守がだれそれ (質問した囚人以外) が処刑されると明かした |
①Wikipedia(日本語版)の「ベイズ推定」の記事 (2010年10月15日現在) ②Wikipedia(英語版)の"Baye's theorem"の記事の"Example 3: The Monty Hall problem"の項 (2010年10月8日版) |
||||
| 不特定事象による条件付確率あるいは事後確率の問題設定 |
[M] 扉1があたり、扉2が当たり、および扉3が当たりのそれぞれの事象 [3] 囚人Aが恩赦、囚人Bが恩赦、および囚人Cが恩赦のそれぞれの事象 |
中間事象の限定なし | 中間事象を証拠事象の一部として計算する解法 |
[M] 挑戦者が扉A を選び、ホストがいずれかのハズレ扉 (A以外) を開けた [3] 囚人X が看守に質問し、看守がいずれかの囚人 (X以外) が処刑されると明かした |
見当たらず | |
|
[M]挑戦者が選んだ扉を特定 [3]看守に質問した囚人を特定 |
中間事象を証拠事象の一部として計算する解法 |
[M] 挑戦者がこれこれの扉を選び、ホストがいずれかのハズレ扉 (挑戦者が選んだ扉以外) を開けた [3] だれそれが看守に質問し、看守がいずれかの囚人 (質問した囚人以外) が処刑されると明かした |
見当たらず | |||
| 中間事象で切り取られた範囲に標本空間を限定して計算する解法 |
[M] ホストがいずれかのハズレ扉 (挑戦者が選んだ扉以外) を開けた [3] 看守がいずれかの囚人 (質問した囚人以外) が処刑されると明かした |
Wikipedia(英語版)の"Monty Hall Probrem"の記事の"Baye's Theorem"の項 (2011年07月23日から09月05日までの版) |
||||
| 非条件付確率の問題設定 |
[M] ホストが扉を開けないケースやホストが挑戦者が選んだ扉を開けてしまうケースを範囲に含めない。あるいは含めたとしても、これらのケースの確率を 0 に限定する。 [3] 看守が答えないケースや看守が質問した囚人の運命を告げるケースを範囲に含めない。あるいは含めたとしても、これらのケースの確率を 0 に限定する。 |
[M] switch すると賞品を得ること [3] 質問した囚人以外の囚人が恩赦であること |
中間事象の限定なし | 中間事象を証拠事象の一部として計算する解法 |
[M] 標本空間の全体 [3] 標本空間の全体 |
①Selvin, Steve (1975a). ②vos Savant, Marilyn (1991). |
|
[M] 挑戦者が選んだ扉を特定 [3] 看守に質問した囚人を特定 |
中間事象で切り取られた範囲に標本空間を限定して計算する解法 |
[M] 標本空間の挑戦者が選んだ扉を特定した範囲 [3] 標本空間の質問した囚人を特定した範囲 |
vos Savant, Marilyn (1990b). |
①特定事象による条件付確率あるいは事後確率の問題設定
ホストが「どれそれ」のハズレ扉を開けたとか、看守が「だれそれ」が処刑されると明かしたとかを、証拠事象として計算する問題設定である。
標本空間の時系列的階層分割やベイズ推定の公式などを使えば機械的に計算できるが、苦労を厭わなければ条件付確率の基礎公式だけで解くこともできる。
中間事象を限定しない場合、つまり挑戦者が選んだ扉や看守に質問した囚人を限定しない場合、樹形図などで標本空間を時系列的階層分割するのも、ベイズ推定の公式を使うのも、かなり面倒になる。ベイズ推定の公式を使った例として、Wikipedia(英語版)の"Monty Hall Probrem"の記事の"Baye's Theorem"の項(2011年09月05日版)がある。
挑戦者が選んだ扉を限定したり、看守に質問した囚人を限定した場合、すなわち中間事象の限定ありの場合には、楽に計算することができる。
特定事象による条件付確率あるいは事後確率の問題設定は、日本語版を含む Wikipedia の各種言語のモンティ・ホール問題の記事において、主要な問題設定とされていて、英語版の"Monty Hall problem"の記事jでは conditional probability solution と呼んでいる。(2010年8月8日現在)
しかしこの問題設定が意味のあるものか、最近(2012年1月)になって私には疑問に思えて来た。下記のような理由からである。
扉2 と扉3 を区別するような問題設定や、看守が名を上げた囚人の名を区別するような問題設定が成り立つためには、そのような観点で分析できるような統計データを集めることができなければならない。しかし、モンティ・ホール問題のゲームで、そのようなデータが揃うか可能性はなさそうである。例えば、Monty Hall による現実のゲームでモンティ・ホール問題のゲームによく似たゲームが行われたことがあったとしても、1回かそこらに過ぎないらしいことが、実際のTV放送の映像を見るとわかる。
標本空間の時系列的階層分割やベイズ推定の公式などを使えば機械的に計算できるが、苦労を厭わなければ条件付確率の基礎公式だけで解くこともできる。
中間事象を限定しない場合、つまり挑戦者が選んだ扉や看守に質問した囚人を限定しない場合、樹形図などで標本空間を時系列的階層分割するのも、ベイズ推定の公式を使うのも、かなり面倒になる。ベイズ推定の公式を使った例として、Wikipedia(英語版)の"Monty Hall Probrem"の記事の"Baye's Theorem"の項(2011年09月05日版)がある。
挑戦者が選んだ扉を限定したり、看守に質問した囚人を限定した場合、すなわち中間事象の限定ありの場合には、楽に計算することができる。
特定事象による条件付確率あるいは事後確率の問題設定は、日本語版を含む Wikipedia の各種言語のモンティ・ホール問題の記事において、主要な問題設定とされていて、英語版の"Monty Hall problem"の記事jでは conditional probability solution と呼んでいる。(2010年8月8日現在)
しかしこの問題設定が意味のあるものか、最近(2012年1月)になって私には疑問に思えて来た。下記のような理由からである。
扉2 と扉3 を区別するような問題設定や、看守が名を上げた囚人の名を区別するような問題設定が成り立つためには、そのような観点で分析できるような統計データを集めることができなければならない。しかし、モンティ・ホール問題のゲームで、そのようなデータが揃うか可能性はなさそうである。例えば、Monty Hall による現実のゲームでモンティ・ホール問題のゲームによく似たゲームが行われたことがあったとしても、1回かそこらに過ぎないらしいことが、実際のTV放送の映像を見るとわかる。
②不特定事象による条件付確率あるいは事後確率の問題設定
ホストが「いずれか」のハズレ扉を開けたことを証拠事象としたり、看守が「いずれか」の処刑される囚人の名を明かしたことを証拠事象として、条件付確率あるいは事後確率を計算する問題設定である。
後述する標準仮定の下では、証拠事象が必ず生起するため、後述の 非条件付確率の問題設定と本質的に違いがなく、数学の確率論を使わなくても「必ず生起する事象は計算に入れなくてよい」というヒューリスティクで解けてしまう。
ただし、当たり扉の配置や恩赦の決め方が等確率でないことがわかっていたり、ホストがハズレ扉を開けるときや、看守が処刑される囚人の名を上げるときのくせがわかっていたりしている場合には、こうした問題設定で確率を計算すると精度が落ちるので、注意が必要である。
このような問題設定を数学的に論ずる人は少ないと考えていたが、Wikipedia(英語版)のMonty Hall Probremの記事の"Baye's Theorem"の項で、 04:03, 23 July 2011の版から約1月間だけ論じられていたので、びっくりした。
後述する標準仮定の下では、証拠事象が必ず生起するため、後述の 非条件付確率の問題設定と本質的に違いがなく、数学の確率論を使わなくても「必ず生起する事象は計算に入れなくてよい」というヒューリスティクで解けてしまう。
ただし、当たり扉の配置や恩赦の決め方が等確率でないことがわかっていたり、ホストがハズレ扉を開けるときや、看守が処刑される囚人の名を上げるときのくせがわかっていたりしている場合には、こうした問題設定で確率を計算すると精度が落ちるので、注意が必要である。
このような問題設定を数学的に論ずる人は少ないと考えていたが、Wikipedia(英語版)のMonty Hall Probremの記事の"Baye's Theorem"の項で、 04:03, 23 July 2011の版から約1月間だけ論じられていたので、びっくりした。
③非条件付確率の問題設定
ホストが「いずれか」のハズレ扉を開けるとか、看守が「いずれか」の処刑される囚人の名を明かすことは、最初から分っていることとして(相場用語なら「折り込み済み」だとして)、確率を計算する問題設定である。
ホストが扉を開かないケースを最初から標本空間に含めないか、含めたとしてもそれらのケースの確率を 0 に限定する点と、 証拠事象によって標本空間の絞込みを行わない点が、「不特定事象による条件付確率あるいは事後確率の問題設定」との大きな違いである。
後述する標準仮定の下では、ホストがどの扉を開くか、あるいは看守が誰の名を明かすかなどは確率に全く影響せず、switch するしないの最終選択と当たり扉の組合せや、質問した囚人と恩赦になる囚人の組み合わせを分類するだけで確率が計算できてしまうので、確率論の知識を必要としない。
ただし、ホストがハズレ扉を開けなかったり、看守が質問に答えてくれない可能性がある場合には、このような問題設定をとることはできない。
当たり扉の配置や恩赦の決め方が等確率でないことがわかっていたり、ホストがハズレ扉を開けるときや、看守が処刑される囚人の名を上げるときのくせがわかっていたりしている場合には、こうした問題設定で確率を計算すると精度が落ちるので、注意が必要である。
Wikipedia(英語版)の"Monty Hall problem"の記事では"unconditional probability solution"や"simple solution"と呼んでいる。(2010年8月8日現在)
ホストが扉を開かないケースを最初から標本空間に含めないか、含めたとしてもそれらのケースの確率を 0 に限定する点と、 証拠事象によって標本空間の絞込みを行わない点が、「不特定事象による条件付確率あるいは事後確率の問題設定」との大きな違いである。
後述する標準仮定の下では、ホストがどの扉を開くか、あるいは看守が誰の名を明かすかなどは確率に全く影響せず、switch するしないの最終選択と当たり扉の組合せや、質問した囚人と恩赦になる囚人の組み合わせを分類するだけで確率が計算できてしまうので、確率論の知識を必要としない。
ただし、ホストがハズレ扉を開けなかったり、看守が質問に答えてくれない可能性がある場合には、このような問題設定をとることはできない。
当たり扉の配置や恩赦の決め方が等確率でないことがわかっていたり、ホストがハズレ扉を開けるときや、看守が処刑される囚人の名を上げるときのくせがわかっていたりしている場合には、こうした問題設定で確率を計算すると精度が落ちるので、注意が必要である。
Wikipedia(英語版)の"Monty Hall problem"の記事では"unconditional probability solution"や"simple solution"と呼んでいる。(2010年8月8日現在)
このようにモンティ・ホール問題や3囚人問題に関する数学的問題設定は何種類もある。後述する「標準仮定」が成立する場合には、当たり扉の設定や、挑戦者の選択、およびホストの行動に対称性があるため、いずれの問題設定でも答えが同一の数値になる。
これらの問題設定ごとに全く別個の問題となっていることを理解するには、統計データを集計して確率を計算する場合に異なった集計方法になることに気付けばよく、集計方法の違いが本質的な違いであることを理解するには、下記のような変形パズルを検討すればよい。
| 変形パズル | 問題設定ごとの解答の食い違い |
|---|---|
| 挑戦者が過去のゲームのデータから、今回の当たり扉を予想することができるという設定の変形パズル | 中間事象を限定する問題設定と、しない問題設定とで、答えが違ってくる。 |
| 挑戦者が当たりを選んだときだけホストが別の扉を開けたり、質問した囚人が恩赦になるときだけ看守が質問に答えたりする変形パズル |
「非条件付確率の問題設定」は考えることができなくなるが、他の問題設定は考えることができる。 |
| ホストが開ける扉や、看守が名を上げる処刑囚に、好みや偏りがあるような変形パズル | 「特定事象による条件付確率あるいは事後確率の問題設定」と、その他の問題設定で答えが一致しないことがある。 |
| 当たり扉の設定や、恩赦になる囚人の選定に偏りがある変形パズル | 挑戦者の選択を特定しない問題設定と特定する問題設定とで答えが一致しないことがある。 |
立場によって数学の問題としてのとらえ方が異なることの説明
モンテイ・ホール問題を例に説明する。(3囚人問題でも同様な説明ができる)
毎回、同一人のホストが同一のゲームを行うゲーム番組を統計マニアが見る場合
その統計マニアはホストの「くせ」を調べようとしてデータを集め、「挑戦者が扉1を選んでホストが扉3を開けた」場合の確率と、「挑戦者が扉1を選んでホストが扉2を開けた」場合の確率を比較しようとするだろう。
これは「特定事象による条件付確率あるいは事後確率の問題設定」に他ならない。
これは「特定事象による条件付確率あるいは事後確率の問題設定」に他ならない。
毎回、同一のゲームを行うが、ホストはちょくちょく交代するゲーム番組を統計マニアでない人が見る場合
switchして当った頻度とハズレた頻度を記憶の中ので比較しようとして、それ以上詳細な分析はしないだろう。
これは「不特定事象による条件付確率あるいは事後確率の問題設定 」に他ならない。
これは「不特定事象による条件付確率あるいは事後確率の問題設定 」に他ならない。
ゲームのルールを聞いて素直に計算する人の場合
「最初にハズレを選ぶとswitchして当る」という法則以外に確率を計算する手がかりは不要である。
これは「非条件付確率の問題設定」に他ならない。
これは「非条件付確率の問題設定」に他ならない。
モンティ・ホール問題のゲームによく似たゲームを初めて見た人の場合
ホストの行動の予想はその人の経験によって変わってくる。
もはや「モンティ・ホール問題」ではない。
もはや「モンティ・ホール問題」ではない。
数学の問題としてのとらえ方の変り種
戦略に着目した問題設定
3囚人問題ではとることのできないモンティ・ホール問題特有の問題設定である。
Let's Make A Deal の入場券を持っているが都合が悪くなって兄弟に代わりに参加してもらうときに、「もしも挑戦者に選ばれたら必ずswitchする」ことを託すときの確率である。
この問題設定は、「ホストが switch させてくれなかったが、もともと当たりの扉を選択していたので賞品を得た」 というケースも計算に含めたり、「ホストが当たり扉を開けてしまってゲームが流れた」 といったケースも計算に含めたりする点が他の問題設定と異なっている。
"Ask Marilyn" の問題文など、モンティ・ホール問題の典型的な問題文を読んで、このような問題設定を当てはめる人は少ない。 しかし、世界で私だけではないかも知れない。 というのはvos Savant, Marilyn (1991).の中で Marilyn vos Savant が提案して、全米の小学校、高校、大学で行われた実験は、switch する戦略と、switch しない戦略のそれぞれで200回ずつ行う実験だから、 もしかしたら、Marilyn vos Savant は非条件付確率の問題設定ではなく、戦略に着目した問題設定をとっているのかも知れない。
「挑戦者が当たりを選んだときだけホストが別の扉を開けたり、質問した囚人が恩赦になるときだけ看守が質問に答えたりする変形パズル」では、他の問題設定と確率の計算結果が食い違うことがある。
後述する標準仮定の下では、「非条件付確率の問題設定」と一致する。
Let's Make A Deal の入場券を持っているが都合が悪くなって兄弟に代わりに参加してもらうときに、「もしも挑戦者に選ばれたら必ずswitchする」ことを託すときの確率である。
| 問題設定のニックネーム | 標本空間の範囲 | 仮説事象 | 中間事象の限定 | 解法の分類 | 証拠事象 | 代表的な論者または文献 |
|---|---|---|---|---|---|---|
| 戦略に着目した問題設定 | ホストが扉を開けないケースやホストが挑戦者が選んだ扉を開けてしまうケースも範囲に含む。 |
switchの機会が与えられたら必ずswitchしようという戦略で賞品を得ること |
中間事象の限定あり/なし | 解法の分類なし | 標本空間の全体 | 見当たらず |
この問題設定は、「ホストが switch させてくれなかったが、もともと当たりの扉を選択していたので賞品を得た」 というケースも計算に含めたり、「ホストが当たり扉を開けてしまってゲームが流れた」 といったケースも計算に含めたりする点が他の問題設定と異なっている。
"Ask Marilyn" の問題文など、モンティ・ホール問題の典型的な問題文を読んで、このような問題設定を当てはめる人は少ない。 しかし、世界で私だけではないかも知れない。 というのはvos Savant, Marilyn (1991).の中で Marilyn vos Savant が提案して、全米の小学校、高校、大学で行われた実験は、switch する戦略と、switch しない戦略のそれぞれで200回ずつ行う実験だから、 もしかしたら、Marilyn vos Savant は非条件付確率の問題設定ではなく、戦略に着目した問題設定をとっているのかも知れない。
「挑戦者が当たりを選んだときだけホストが別の扉を開けたり、質問した囚人が恩赦になるときだけ看守が質問に答えたりする変形パズル」では、他の問題設定と確率の計算結果が食い違うことがある。
後述する標準仮定の下では、「非条件付確率の問題設定」と一致する。
問題の解法の変り種
2013/07/30 この箇所を修正しました。
Wikipedia(ロシア語版)の "Парадокс Монти Холла"(モンティ・ホール パラドックス)の記事の 16:22, 27 февраля 2010 の版から使われている図は、そういった珍しい例の一つである。
扉の選び方や switch するかしないかによる結果の違いを表している。
Wikipedia(ロシア語版)の "Парадокс Монти Холла"(モンティ・ホール パラドックス)の記事の 16:22, 27 февраля 2010 の版から使われている図は、そういった珍しい例の一つである。
扉の選び方や switch するかしないかによる結果の違いを表している。
OU Math Club というサイトの "What are the odds, part II" という記事の場合
こちらの方は、switch する場合に限定して確率を計算しているので、Wikipedia(ロシア語版)の場合より簡素な図となっている。
別種の確率変数を採用した問題設定・・・というより新種のモンティ・ホール問題や新種の3囚人問題
モンティ・ホール問題でハズレの賞品がある場合には、扉の中のハズレ賞品に番号を着けることができる。
3囚人問題で処刑される囚人の処刑方法が異なっていたり、処刑が同時ではなく順番に行われたりする場合には、処刑内容を区別することができる。
こうした場合、通常とは異なる確率変数で問題を考えることができる。
ただし、モンティ・ホール問題の場合、ハズレ賞品があるとは限らないし、3囚人問題の場合も処刑内容が区別できるとは限らないので、問題の構造は同一であるが、まったく別の新種の問題を解いていることになる。
変り種の確率変数では扉の区別や、囚人の区別が確率に影響するような変形パズルに対する分析力無くなってしまっている。
標本空間のレベルでは、ハズレの賞品や処刑内容を区別しているため標準的な標本空間より大きくなってしまっている。
しかし、通常の確率変数ではハズレや処刑内容の区別がなく、変り種の確率変数では扉や囚人の区別がないので、事象の集合のレベルでは標準的な方法と同レベルのサイズになる。
こうした変り種の問題設定を、 Wikipedia(英語版)の "Monty Hall problem" の記事の 2007/03/24 02:16 の版から 2008/05/11 20:15 の版に掛けてと、 2012/ 1/ 19 16:45 の版から最新版 (2012年11月24日現在)に掛けての版で見ることができる。
2012/11/22 17:34 の版の 「2.5 'The Economist'」 の項の場合、 人の顔と手のイラストが描き込まれた説明図をよく見ると、 "Goat A"、"Goat B" のようにヤギを区別している。
Wikipedia(日本語版)の「モンティ・ホール問題」の記事(2011年4月28日 (木) 2334の版)の、「ハズレに色を付ける方法」の項でも同様な説明を見ることができる。
これらでは、ハズレを示す賞品としての2頭のヤギが存在し、2頭のヤギが区別できるものとして次のように議論されている。
扉に対する賞品の配置を意識しながら2頭のヤギを区別したら、賞品の配置という確率変数の値域が2倍に拡大してしまうが、 日本語版の説明文も、 英語版の説明図も、 そうしたことを免れている。
3囚人問題で処刑される囚人の処刑方法が異なっていたり、処刑が同時ではなく順番に行われたりする場合には、処刑内容を区別することができる。
こうした場合、通常とは異なる確率変数で問題を考えることができる。
ただし、モンティ・ホール問題の場合、ハズレ賞品があるとは限らないし、3囚人問題の場合も処刑内容が区別できるとは限らないので、問題の構造は同一であるが、まったく別の新種の問題を解いていることになる。
|
モンティ・ホール問題 |
3囚人問題 |
|
|---|---|---|
|
|
|
|
|
通常の 確率変数 |
|
|
|
変り種の 確率変数 |
|
|
変り種の確率変数では扉の区別や、囚人の区別が確率に影響するような変形パズルに対する分析力無くなってしまっている。
標本空間のレベルでは、ハズレの賞品や処刑内容を区別しているため標準的な標本空間より大きくなってしまっている。
しかし、通常の確率変数ではハズレや処刑内容の区別がなく、変り種の確率変数では扉や囚人の区別がないので、事象の集合のレベルでは標準的な方法と同レベルのサイズになる。
こうした変り種の問題設定を、 Wikipedia(英語版)の "Monty Hall problem" の記事の 2007/03/24 02:16 の版から 2008/05/11 20:15 の版に掛けてと、 2012/ 1/ 19 16:45 の版から最新版 (2012年11月24日現在)に掛けての版で見ることができる。
Wikipedia(日本語版)の「モンティ・ホール問題」の記事(2011年4月28日 (木) 2334の版)の、「ハズレに色を付ける方法」の項でも同様な説明を見ることができる。
これらでは、ハズレを示す賞品としての2頭のヤギが存在し、2頭のヤギが区別できるものとして次のように議論されている。
| 自動車 | ヤギ1 | ヤギ2 | switch の結果 | |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
扉に対する賞品の配置を意識しながら2頭のヤギを区別したら、賞品の配置という確率変数の値域が2倍に拡大してしまうが、 日本語版の説明文も、 英語版の説明図も、 そうしたことを免れている。
そもそも数学の問題たりえないとするとらえ方
Whitaker, Craig F. (1990). が"Ask Marilyn"に投稿した問題文や、市川 伸一, 下條 信輔. (2010).が紹介した3囚人問題の問題文など、主要な問題文において、確率計算に必要な条件の既述が不足している。
たとえば、「挑戦者がどの扉を選んでもホストは挑戦者が選ばなかったハズレの扉を必ず開ける」とは明記されていないし、「どの囚人が看守に質問しても看守は質問した囚人以外の処刑される囚人の名を必ず答える」とも明記されていない。
つまり、これらの問題文では数学の問題として"well defined"でない。
このことを重視してモンティ・ホール問題や3囚人問題は数学の問題たりえないとするとらえ方もある。
たとえば、「挑戦者がどの扉を選んでもホストは挑戦者が選ばなかったハズレの扉を必ず開ける」とは明記されていないし、「どの囚人が看守に質問しても看守は質問した囚人以外の処刑される囚人の名を必ず答える」とも明記されていない。
つまり、これらの問題文では数学の問題として"well defined"でない。
このことを重視してモンティ・ホール問題や3囚人問題は数学の問題たりえないとするとらえ方もある。
数学の問題としてのとらえ方の違いを、単なる解法の違いだと解釈する人もいる
2013/05/31 にこの項の記述を大幅に訂正しました。
2016/08/21 にもかなり大きく修正しました。
Wikipedia(英語版)の "Monty Hall problem" の記事 (20:04, 18 December 2012.の版) を読むと、
モンティ・ホール問題を条件付確率の問題としてとらえるとらえ方と、 非条件付確率の問題としてとらえるとらえ方の違いを、
単なる解法の違いと解釈しているのか、 別個の問題設定としてとらえているのか、あいまいに見える。
記事全体を通して見ると 「単なる解法の違い」 という立場のように (私には) 見えたのであるが、 "Criticism of the simple solutions" の項は別のトーンで書かれているように見える。
この項では、「非条件付き確率の問題として解いたのでは正解にならない」 という説や、「非条件付き確率の問題の解き方と条件付き確率の問題の解き方で答えが異なる場合がある」 という説を紹介している。
Bell, William (1992). が標準仮定の下ではどちらのとらえ方でも答えが一致すると述べていることも紹介しているが、 最後の方で、「ホストが必ずハズレの扉を開けるから挑戦者の扉が当たりの確率は変わらない」 という考え方の誤りにも触れている。
そして、"Criticism of the simple solutions" の項の最後の最後を次のように締めくくっている。
このことから、Wikipedia(英語版)の "Monty Hall problem" の記事 (20:04, 18 December 2012.の版) の"Criticism of the simple solutions" の項では次のような主張が優勢であるようだ。
2016/08/21 にもかなり大きく修正しました。
Wikipedia(英語版)の "Monty Hall problem" の記事 (20:04, 18 December 2012.の版) を読むと、
モンティ・ホール問題を条件付確率の問題としてとらえるとらえ方と、 非条件付確率の問題としてとらえるとらえ方の違いを、
単なる解法の違いと解釈しているのか、 別個の問題設定としてとらえているのか、あいまいに見える。
記事全体を通して見ると 「単なる解法の違い」 という立場のように (私には) 見えたのであるが、 "Criticism of the simple solutions" の項は別のトーンで書かれているように見える。
この項では、「非条件付き確率の問題として解いたのでは正解にならない」 という説や、「非条件付き確率の問題の解き方と条件付き確率の問題の解き方で答えが異なる場合がある」 という説を紹介している。
Bell, William (1992). が標準仮定の下ではどちらのとらえ方でも答えが一致すると述べていることも紹介しているが、 最後の方で、「ホストが必ずハズレの扉を開けるから挑戦者の扉が当たりの確率は変わらない」 という考え方の誤りにも触れている。
そして、"Criticism of the simple solutions" の項の最後の最後を次のように締めくくっている。
我々や問題文中のプレーヤーにとって、ホストが開ける扉をどうやって選ぶかまったくわからないので、対称性の原理から半々の確率を与えるしかない。 対称性の原理から扉の番号を特定することにも意味がない。
(意訳というより私の理解した内容に書き直しています)
(意訳というより私の理解した内容に書き直しています)
このことから、Wikipedia(英語版)の "Monty Hall problem" の記事 (20:04, 18 December 2012.の版) の"Criticism of the simple solutions" の項では次のような主張が優勢であるようだ。
- 解法の違いは解こうとしている問題自体が異なることに対応する。
- 開けた扉を特定しない問題のとらえ方にも正当性がある。
心理学の問題としてのとらえ方
モンティ・ホール問題や3囚人問題は、確率論の訓練を受けていなければ、ほとんどの人が解けない問題である。
このような心の働きが認知心理学の研究テーマとなっていて、次のような観点で研究されている。
・確率の錯覚をもたらすヒューリスティクに関する研究
- ※条件付確率や事後確率の知識の無い一般の人の正答率の低さが、数多くの心理学実験で明らかになっている。
- ※一般の人でも、麻雀やコントラクト・ブリッジ、あるいは株や通貨の相場に強い人は容易に解くことができるかも知れない。
このような心の働きが認知心理学の研究テーマとなっていて、次のような観点で研究されている。
・確率の錯覚をもたらすヒューリスティクに関する研究
・課題の与え方と正答率の関係など、ヒューリスティクの特徴に関する研究
・年齢による正答率の変化など、ヒューリスティクの発達心理学的研究
・年齢による正答率の変化など、ヒューリスティクの発達心理学的研究
成長の過程で身に付けた無意識の判断プロセス、すなわち「ヒューリスティク」が自動的に答えを出すので、自分にも解ける問題だと錯覚したり、正解を説明されても納得できないのだという説がある。
・知能レベルと正答率の関係に関する研究 ( 関係ないという報告も、あるという報告もある )
・反復による学習効果の実験 ( ハトと大学生を競争させた実験が有名 )
・反復による学習効果の実験 ( ハトと大学生を競争させた実験が有名 )
その他のとらえ方
素人解法もしくは素人説明のコレクションとしてのとらえ方
素朴で日常的な確率概念の範囲で理解できるような解き方が色々と考案されている。「非条件付確率の問題設定」など条件付確率や事後確率の知識を必要としない問題設定でなければそのような解きかたは不可能であり、実際、そのような問題設定が多い。
しかし中には「特定事象による条件付確率あるいは事後確率の問題設定」で解答しているつもりになっているが、「不特定事象による条件付確率あるいは事後確率の問題設定 」で解いているのか何なのか、とんちんかんな解答になってしまったものもある。
このような素人解法もしくは素人説明をコレクションすることも、モンティ・ホール問題や3囚人問題のマニアの楽しみである。
しかし中には「特定事象による条件付確率あるいは事後確率の問題設定」で解答しているつもりになっているが、「不特定事象による条件付確率あるいは事後確率の問題設定 」で解いているのか何なのか、とんちんかんな解答になってしまったものもある。
このような素人解法もしくは素人説明をコレクションすることも、モンティ・ホール問題や3囚人問題のマニアの楽しみである。
歴史的事件としてのとらえ方
モンティ・ホール問題が有名になった背景には、PARADEという日曜ニュース雑誌に掲載されている"Ask Marillyn"というコラムで大激論が行われ、コラムのオーナーである Marilyyn vos Savant が出した答えは間違いだと大勢の数学博士が勘違いした事件が関係している。
この事件に関する経緯や、エピソードを調べると興味が尽きない。
(Tierney, John (1991).に詳しく書かれている)
自己流問題文のコレクションとしてのとらえ方
モンティ・ホール問題を理解したつもりの人が他の人に出題するとき、自己流の問題文を作ることが多い。そのような場合、標準仮定のあやしい問題文や、標準仮定が成立しない問題文になることがある。
こういった似非モンティ・ホール問題を収集することも、マニアの楽しみである。
こういった似非モンティ・ホール問題を収集することも、マニアの楽しみである。
デマのコレクションとしてのとらえ方
インターネットで見かけるモンティ・ホール問題の解説には、デマがあふれている。そのようなデマをコレクションすることは、マニアにとって楽しくはないが、避けては通れない。
確率解釈論の題材としてのとらえ方
モンティ・ホール問題や3囚人問題では、統計調査の困難な確率が重要な働きをしている。
当たり扉や恩赦囚人の決め方、挑戦者が選ぶ扉や看守に質問する囚人の決まり方、ホストがハズレ扉を開けたり看守が質問に答えたりするか否か、ホストが開ける扉や看守が名を上げる囚人の決め方、等々
しかし、Let's Make A Deal でモンティ・ホール問題によく似たゲームが行われた回数は多くない。(もしかしたら Steve Selvin が見た1回ぽっきりかも知れない) 3囚人問題について言うならば、例えば何度も囚人が3人ずつ処刑されることになって、何度も一人だけ恩赦になって、何度も一人の囚人が看守に質問するという状況が現実に起きるとは考えられない。 そうすると、モンティ・ホール問題や3囚人問題を解くときの材料として使っている確率は何なのか気になってくる。
また別の悩みもある。
特定事象による条件付確率あるいは事後確率の問題設定 で得られる条件付き確率が 「結果を予想する確率」 でなく、 「原因を予想する確率」 であるため、 「主観確率」 と呼んで特別扱いするべきだと論じる人もいる。 しかし数学の確率論の上ではこうした条件付き確率を通常の条件付き確率と区別する理由が無い。
こういった悩みを考える分野が「確率解釈論」 (probability interpletations) で、モンティ・ホール問題や3囚人問題にハマッた人が迷いこむ迷路の一つである。
当たり扉や恩赦囚人の決め方、挑戦者が選ぶ扉や看守に質問する囚人の決まり方、ホストがハズレ扉を開けたり看守が質問に答えたりするか否か、ホストが開ける扉や看守が名を上げる囚人の決め方、等々
しかし、Let's Make A Deal でモンティ・ホール問題によく似たゲームが行われた回数は多くない。(もしかしたら Steve Selvin が見た1回ぽっきりかも知れない) 3囚人問題について言うならば、例えば何度も囚人が3人ずつ処刑されることになって、何度も一人だけ恩赦になって、何度も一人の囚人が看守に質問するという状況が現実に起きるとは考えられない。 そうすると、モンティ・ホール問題や3囚人問題を解くときの材料として使っている確率は何なのか気になってくる。
また別の悩みもある。
特定事象による条件付確率あるいは事後確率の問題設定 で得られる条件付き確率が 「結果を予想する確率」 でなく、 「原因を予想する確率」 であるため、 「主観確率」 と呼んで特別扱いするべきだと論じる人もいる。 しかし数学の確率論の上ではこうした条件付き確率を通常の条件付き確率と区別する理由が無い。
こういった悩みを考える分野が「確率解釈論」 (probability interpletations) で、モンティ・ホール問題や3囚人問題にハマッた人が迷いこむ迷路の一つである。
エンタテインメントの素材としてのとらえ方
モンティ・ホール問題はテレビの教育番組や教養娯楽番組で取り上げられることもある。このような場合にどのような教材が使われるか、どのような解説をしているか、という観点で見ると面白い。
また、ドラマ番組、小説、漫画などで主人公が解決すべき問題として登場することもある。このような場合にどのような状況設定になっているか、などの観点で見ると面白い。
また、ドラマ番組、小説、漫画などで主人公が解決すべき問題として登場することもある。このような場合にどのような状況設定になっているか、などの観点で見ると面白い。
もう一つのモンティ・ホール問題(モンティ・ホール問題のワーディングの議論)
モンティ・ホール問題の最も有名な問題文である"Ask Marilyn"の問題文 から標準仮定だけを読み取ることに疑義を唱える人たちがいる。
注:"Ask Marilyn"の問題文とは、PARAD誌のコラム"Ask Marilyn"にWhitaker, Craig F. (1990). さんが投稿したもので、モンティ・ホール問題が有名になるきっかけになった。
こういう人たちは数学パズルを数学の問題と同レベルの厳密さで解こうとしているのかも知れない。
あるいは、ホストが開ける扉のえり好みによって答えが違ってくるという発見に驚いて他の人に伝えたがっているのかも知れない。
あるいは、"Ask Marilyn"の問題文冒頭の "Suppose you're on a game show, and you 're given the choice of three doors. という文にとらわれて、問題文に書かれている情景がホストの行動規則でなく、そのとき限りのエピソードを表していると解釈しているのかも知れない。
あるいは、なまじっか、Monty Hall がホストを務める実際のゲームをTV放送で見たことがあるばっかりに、Monty Hall が自分の行動ルールを述べていないことを重視しているのかも知れない。
あるいは、自分がゲーム番組の挑戦者に選ばれたらどうしようと、本気で心配しているのかも知れない。
あるいは、自分がホスト役になって実演したときに、挑戦者役が当たりを選んだときの自分のハズレの開け方がランダムでないことに気付いたのかも知れない。
あるいは、「無意識の仮定」という心理現象にかまけることで、「確率の錯覚」の不思議さから目をそらそうとしているのかも知れない。
あるいは、ワーディングの議論に私の知らない意義を見出しているのかも知れない。
いずれにせよ、このような人たちには"Ask Marilyn"の問題文が次のように見えるらしい。
あなたがゲーム番組の挑戦者に選ばれた。
あなたに3つの扉が示された。
そのうちの1つに賞品が隠されている。
賞品を隠す扉の決め方が均等だとは限らない
ホストがあなたに一つの扉を選ばせた。
ホストはどこに賞品が隠されているか知っている。
その知識をどのように利用したかわからない
ホストは別のハズレの扉を一つ開けた。
いつも開けるとは限らない
ハズレしか開けないとは限らない
あなたが選んだ扉を開けないとは限らない
あなたが当たりを選んだときに、ホストが開ける扉に偏りが無いとは限らない
あなたはもう一つの扉に切り替えてもよいと言われた。
言われるとは限らない
あなたはどうすべきか?
このようにモンティ・ホール問題をとらえて議論することを「ワーディングの議論」と呼ぶ。
ワーディングの議論は以下のタイプに分かれる。
モンティ・ホール問題に答えはないとするタイプ(数学者など)
1991年に New York Times のTierney, John (1991).による取材の中で Diaconis は、ホストの行動の動機がわからなければこの問題には答えられないと述べている。
非条件付確率の解答の誤りや、 標準仮定だけに依拠した解答の不完全さを示すために議論するタイプ(数学者など)
1992年以降に、"Ask Marilyn" の問題文をさまざまに解釈して論文を書いた数学者たちは、非条件付確率の解答 は 標準仮定の下でしか成り立たないから誤りだとか、標準仮定だけの議論では不十分だとか言いたいらしい。 ただし、 非条件付確率の解答 と 特定事象による条件付確率あるいは事後確率の解答 が一致する条件を明らかにするという数学的興味で論じている人もいないわけではない。
補足
Wikipedia(英語版)の "Monty Hall problem" の記事 (2012年3月19日20:49版) の "Criticism of the simple solutions" の項で、非条件付き確率の解答の誤りを指摘する人たちの言葉が引用されている。 彼らの言葉を読むと、"Ask Marilyn" の問題文の中で挑戦者が開けた扉の番号やホストが開けた扉の番号を例示していることに引きずられて、 「条件付き確率の問題として解くことを問題文が要求している」 と解釈しているらしいことが分る。
補足
Wikipedia(英語版)の "Monty Hall problem" の記事 (2012年3月19日20:49版) の "Criticism of the simple solutions" の項で、非条件付き確率の解答の誤りを指摘する人たちの言葉が引用されている。 彼らの言葉を読むと、"Ask Marilyn" の問題文の中で挑戦者が開けた扉の番号やホストが開けた扉の番号を例示していることに引きずられて、 「条件付き確率の問題として解くことを問題文が要求している」 と解釈しているらしいことが分る。
心理学の実験材料として論じるタイプ(認知心理学者など)
モンティ・ホール問題や3囚人問題を認知心理学的に研究するときに、問題文の曖昧さが標準仮定の認識や正答率にどのように影響するか、実験で確かめることが行われている。
確率が問題になる人生の局面での警告として論じるタイプ(行動経済学者など)
確率計算の材料として使う条件を無意識に仮定してしまい、その仮定が誤っていたために条件付確率の計算結を誤ることの事例として、モンティ・ホール問題を取り上げた論文がある。条件付き確率の知識を駆使して計算したつもりでも確率判断を誤ることがあることを警告しているのだろう。
問題文の曖昧さを根拠に、日常の確率概念の問題にすり替えようとするタイプ
「ホストの行動規則が明示されていないから、残った扉が当りである確率がどちらも 1 / 2 だと考えてもおかしくない」 と述べる人もいる。
そのような考えが成立するのは数学の確率概念の世界でなく、日常の確率概念の世界であることに本人は気付いていない。
そのような考えが成立するのは数学の確率概念の世界でなく、日常の確率概念の世界であることに本人は気付いていない。
さらにもう一つのモンティ・ホール問題(ノンフィクション・モンティ・ホール問題)
1975年に Steve Selvin がモンティ・ホール問題を発表したのは、3囚人問題をゲーム番組に当てはめた新しい数学パズルを作ることが目的ではなく、純粋にゲーム番組のゲームに統計数学の手法を応用してみたかったのだと解釈して、Steve Selvin になりかわって Let's Make A Deal のゲームを分析してやろうという人が居るかも知れない。
実際、それに近いことをやっている人がいる。例えば Friedman, D. (1998). という人が、Monty Hall が常に挑戦者に switch の機会を与えていたのか知りたくて、Monty Hall 本人に質問したり、Let(s Make A Deal の映像資料を調べたりしている。
実際、それに近いことをやっている人がいる。例えば Friedman, D. (1998). という人が、Monty Hall が常に挑戦者に switch の機会を与えていたのか知りたくて、Monty Hall 本人に質問したり、Let(s Make A Deal の映像資料を調べたりしている。
さらにさらにもう一つのモンティ・ホール問題(リアル版・モンティ・ホール問題)
モンティ・ホール問題のゲームを実際に行った場合に標準仮定からどのくらいズレるのか気になるときがある。
実演形式でモンティ・ホール問題の説明をしている人を動画サイトで見ながら、マジシャンズチョイスの原理を思い出したときがそうである。
※マジシャンスチョイスの代表として、手品師が差し出したカードの中から1枚を選ぶときは真ん中を選ぶことが多いという法則がある。
当たり扉の配置や、挑戦者の扉の選択、ホストによるハズレ扉の開け方に関する確率配分の組合せによっては、switch して賞品を得る確率が標準仮定の下での値から大きくズレるかも知れない。
実演形式でモンティ・ホール問題の説明をしている人を動画サイトで見ながら、マジシャンズチョイスの原理を思い出したときがそうである。
※マジシャンスチョイスの代表として、手品師が差し出したカードの中から1枚を選ぶときは真ん中を選ぶことが多いという法則がある。
当たり扉の配置や、挑戦者の扉の選択、ホストによるハズレ扉の開け方に関する確率配分の組合せによっては、switch して賞品を得る確率が標準仮定の下での値から大きくズレるかも知れない。
さらにさらにさらにもう一つのモンティ・ホール問題(ありのまま版・モンティ・ホール問題)
ホストや挑戦者がモンティ・ホール問題の問題文に書かれているゲームの描写のありのままがゲームのルールだと考えて行動する場合を考えると、 問題文がどんなに曖昧でも確率を論じることができる。
たとえば学生を沢山集めて二人ずつに分け、それぞれの組ごとに、 一人がホスト、もう一人が挑戦者になって問題文に出てくるゲームを行わせるような実験が考えられる。
彼らには、国語の理解力のテストだとか言って、正確に問題文のとおりに行動することを求めればよい。
この実験に参加すると講義の出席を何時間か免除されるようにすれば学生も集まるだろう。
実験には、もっとも有名な "Ask Marilyn" の問題文を使うのが相応しいだろう。
このような実験をすると、関東では switch する方が有利で、関西では switch しない方が有利になるかも知れない。
たとえば学生を沢山集めて二人ずつに分け、それぞれの組ごとに、 一人がホスト、もう一人が挑戦者になって問題文に出てくるゲームを行わせるような実験が考えられる。
彼らには、国語の理解力のテストだとか言って、正確に問題文のとおりに行動することを求めればよい。
この実験に参加すると講義の出席を何時間か免除されるようにすれば学生も集まるだろう。
実験には、もっとも有名な "Ask Marilyn" の問題文を使うのが相応しいだろう。
このような実験をすると、関東では switch する方が有利で、関西では switch しない方が有利になるかも知れない。
さらにさらにさらにさらにもう一つのモンティ・ホール問題(ゲーム理論の題材としてのモンティ・ホール問題)
挑戦者側が当たりを選んだときのハズレ扉の開け方をホスト側の戦略とした場合
Seymann R. G. (1991). や Gill, Richard D.(2010). 、 Gill, Richard (2011) などの文献では、ホストや挑戦者をゲーム理論のプレイヤーに見立てる考え方にも触れているが、「まったく当たりを出さないこと」 をホストの目標にしているので、テレビ番組のゲームになじまず、違和感が残る。
それはともかくとして、Gill, Richard D.(2010). の中で、 「まったく当たりを出さないこと」 をホスト側の目標をとした上で、挑戦者が当たりを選んだときのハズレ扉のどちらを開けるかをホスト側の戦略としてゲーム理論的な分析を行って、挑戦者側が常に switch する戦略をとった場合、ホスト側の戦略に無関係に確率2/3 で挑戦者側が賞品を得ることを導いている。
それはともかくとして、Gill, Richard D.(2010). の中で、 「まったく当たりを出さないこと」 をホスト側の目標をとした上で、挑戦者が当たりを選んだときのハズレ扉のどちらを開けるかをホスト側の戦略としてゲーム理論的な分析を行って、挑戦者側が常に switch する戦略をとった場合、ホスト側の戦略に無関係に確率
「地獄から来たモンティ」として振る舞う割合をホスト側の戦略とした場合
ホスト側の目標を 「適性な頻度で挑戦者に大当たりを出す」 ことであるとすれば、テレビ番組の中のゲームになじむ形でゲーム理論が適用できる。
番組の放送ごとに交代するかも知れないホストの総体を 1つのプレイヤーとしてとらえ、番組の放送ごとに次から次に現れる挑戦者の総体を 1つのプレイヤーとしてとらえ、大当たりのでる適正な頻度がスポンサー企業と の相談で決まっているとして、ホストが 「地獄から来たモンティ」として振る舞う割合と、標準仮定に従って振る舞う割合の設定をホスト側の戦略としてとらえ、挑戦者が switch する割合と stay する割合を挑戦者側の戦略としてとらえると、ゲーム理論の題材になりそうである。
現実のTV番組のホストはその回までに当りが出たペースに応じて戦略を変えるのであって、挑戦者たちの戦略そのものに反応するわけではないし、 挑戦者たちも一つのチームになっているわけではないが、理論上は上記のような 2プレイヤーゲームと見なせるだろう。
ただし、ホストが「地獄から来たモンティ」としてあからさまに振る舞うことはなさそうなので、あくまでも理論上の話である。
番組の放送ごとに交代するかも知れないホストの総体を 1つのプレイヤーとしてとらえ、番組の放送ごとに次から次に現れる挑戦者の総体を 1つのプレイヤーとしてとらえ、大当たりのでる適正な頻度がスポンサー企業と の相談で決まっているとして、ホストが 「地獄から来たモンティ」として振る舞う割合と、標準仮定に従って振る舞う割合の設定をホスト側の戦略としてとらえ、挑戦者が switch する割合と stay する割合を挑戦者側の戦略としてとらえると、ゲーム理論の題材になりそうである。
現実のTV番組のホストはその回までに当りが出たペースに応じて戦略を変えるのであって、挑戦者たちの戦略そのものに反応するわけではないし、 挑戦者たちも一つのチームになっているわけではないが、理論上は上記のような 2プレイヤーゲームと見なせるだろう。
ただし、ホストが「地獄から来たモンティ」としてあからさまに振る舞うことはなさそうなので、あくまでも理論上の話である。
さらにさらにさらにさらにさらにもう一つのモンティ・ホール問題(ベイズ改定の題材としてのモンティ・ホール問題)
Hogbin, M. and Nijdam, W. (2010).では、
挑戦者が当たり扉を選んだときにホストが残りの扉のどちらを開けるかの確率分布のパラメータの事前分布を考えてから、
ホストが開けた扉を証拠事象としてそれをベイズ改定し、
改定後の確率分布の上で、ホストが開けた扉を証拠事象として残った扉が当たりである事後確率を計算するという試みをしている。
挑戦者が当たり扉を選んだときにホストが残りの扉のどちらを開けるかの確率分布のパラメータの事前分布を考えてから、
ホストが開けた扉を証拠事象としてそれをベイズ改定し、
改定後の確率分布の上で、ホストが開けた扉を証拠事象として残った扉が当たりである事後確率を計算するという試みをしている。
あえて数学用語の統一はしない
挑戦者が扉1を選びホストが扉3を開けた後の扉1が当たりの確率や、囚人Aに質問された看守が囚人Bが処刑されると言った後の囚人Aが恩赦になる確率を、確率論では、「条件付確率」とよんだり「事後確率」と呼んだりする。
「事後確率」という用語は、ベイズ推定やベイズの定理などを使う場合の用語である。
モンティ・ホール問題や3囚人問題はベイズ推定やベイズの定理を使わずに解くことも可能であることから、この資料では「事後確率」の用語と合わせて「条件付確率」という用語も使用することとする。
「事後確率」という用語は、ベイズ推定やベイズの定理などを使う場合の用語である。
モンティ・ホール問題や3囚人問題はベイズ推定やベイズの定理を使わずに解くことも可能であることから、この資料では「事後確率」の用語と合わせて「条件付確率」という用語も使用することとする。
モンティ・ホール問題と3囚人問題の問題文
モンティ・ホール問題の典型的な問題文
モンティ・ホール問題の典型的な問題文として、当時数学の先生だったらしい Craig F.Whitaker という人が、PARADE という雑誌のコラム "Ask Marilyn" に投稿した問題文を示す。
この問題文に回答した Marilyn vos Savant も、彼女の回答に反論した読者(の大部分)も次のような仮定の上で議論していた。ゲーム番組にあなたが出演していて、三つの扉のどれかを選択できると仮定してください。 一つの扉の後ろに自動車があり、残りの扉の後ろにはそれぞれヤギがいます。 あなたは一つの扉、たとえば扉1を選び、どの扉の後ろに何があるか知っているホストは、 ヤギがいると知っている別の扉、たとえば扉3を開けます。 彼はあなたに言います。「扉2にしたいですか?」 選択を switch する方があなたにとって有利でしょうか? クレイグ F. ホウィタカー メリーランド州クリーブランド ---Whitaker, Craig F. (1990). から翻訳
- ①当たり扉はランダムかつ等確率に設定される
- ②ホストは挑戦者の選んだ扉を開けない
- ③ホストは必ず残りの扉を一枚開ける
- ④ホストはハズレの扉しか開けない
- ⑤ホストは挑戦者の選んだ扉が当たりのとき、ハズレ扉をランダムかつ等確率に選んで開ける
(この仮定を以後「等確率開扉の仮定」と呼ぶこととする) - ⑥ホストは扉を開けた後に必ずswitchの機会を挑戦者に与える
このような仮定を「標準仮定」と呼ぶ。
「標準仮定」 (the standard assumptions)とは、Wikipedia(英語版)の "Monty Hall problem" の記事で導入された用語であるが、便利なので使わせていただく。
標準仮定のもとでは switch して賞品を獲得する確率が 2/3 となるので、switch した方が有利という解答が正解になる。
標準仮定の一部の 「等確率開扉の仮定」 を緩めても、switch して賞品を獲得する確率が 1/2~1 となるので、switch した方が有利である。
上記の "Ask Marilyn" の問題文から標準仮定を読み取る人が大部分であるが、中には標準仮定が曖昧だと難癖を付ける人もいるので、標準仮定を併記することで、そういった連中の顔を立てながら議論することが多い。
"Ask Marilyn" の問題文は、Wikipediaの英語版、フランス語版、イタリア語版、スペイン語版、ロシア語版など、多数の版の「モンティ・ホール問題」 の記事の中で、問題文として採用されている。(2010年8月8現在)
オランダ語版でも 2009年2月21日 22:45 の版から "Ask Marilyn" の問題文に切り替わり、ドイツ語版でも遅ればせながら 2010年10月29日 20:03 の版から、"Ask Marilyn" の問題文に切り替わった。
日本語版の「モンティ・ホール問題」の記事(2011年5月14日現在)の問題文は、いまだに Wikipedia(英語版)の "Monty Hall Problem" の記事の23:56, 19 June 2003 の版の問題文をベースにしていて"Ask Marilyn"のの問題文をベースにしていない。
"Ask Marilyn" の問題文を採用していない版は他にポルトガル語版やポーランド語版があるが、国際的に少数派である。(2011年5月14日現在)
このように、国際的にモンティ・ホール問題の基準とされている"Ask Marilyn"の問題文の中に Monty Hall の名が出て来ない。それにも関わらず「モンティ・ホール問題」と呼ばれるようになった経緯については、モンティ・ホール問題の歴史の項を読んでいただきたい。
「モンティ・ホール問題」以外のモンティ・ホール問題の名称
不思議さを反映した名称で呼ばれることもある。
モンティ・ホール・ディレンマ (the Monty Hall dilemma)
モンティ・ホール・パラドックス (the Monty Hall paradox)
モンティ・ホール・パラドックス (the Monty Hall paradox)
1990~1991の "Ask Marilyn"での論争時には、コラムのオーナー Marilyn vos Savant は次のように呼称していた。
ゲーム番組問題 (The Game Show Problem)
"Ask Marilyn"での論争にちなんで付けられた名称もある。
マリリンとヤギ (Marilyn and the Goats)
"Ask Marilyn"の問題文の内容に基づいた名称もある。
自動車とヤギ問題 (the problem of the Car and Goats)
ヤギ問題 (Ziegenproblem)
ヤギ問題 (Ziegenproblem)
「3囚人問題」をもじった名称もある。
3扉問題 (Three doors problem)
Aha! Gotcha book (Gardner, Martin (1982). )の中にある 3個の胡桃の殻とエンドウ豆 1つを使ったパズルもモンティ・ホール問題の一つに数えたい。
3個の殻ゲーム (Three Shell Game)
元来、"Three Shell Game" という名称は胡桃の殻とエンドウ豆を使ったいかさま博打や手品を表す言葉であって、パズルとは縁遠い。 (駄洒落です) 「3個の殻ゲーム」 という名称をどうしても使いたいなら 「3個の殻ゲーム風モンティ・ホール問題」 に変えるのがよいだろう。
3囚人問題(Three Prisoners problem)の典型的な問題文
市川 伸一, 下條 信輔. (2010).によると、3囚人問題は1950年代から知られている作者不詳の問題で、一般的に次のような問題文で紹介されるらしい。
3囚人問題は、1959年に、Scientific American 誌の Martin Gardner のコラム "Mathematical Games" で取り上げられている。
(Gardner, Martin (1959a).;Gardner, Martin (1959b).)
モンティ・ホール問題に比べて、3囚人問題の人気は薄い。
標準仮定の元で、Aの釈放される確率は1/3のままで、Cの釈放される確率が2/3になる。3人の囚人A,B,Cがいる。1人が恩赦になって釈放され、残りの2人が処刑されることが分っている。 だれが恩赦になるか知っている看守に対し、Aが 「BとCのうち少なくとも1人処刑されるのは確実なのだから、2人の中で処刑される1人の名前を教えてくれても 私についての情報を与えることにはならないだろう。1人を教えてくれないか」 と頼んだ。看守はAの言い分に納得して、「Bは処刑されるよ」と答えた。 それを聞いたAは、「これで自分の助かる確率は1/3から1/2に増えた」と喜んだという。 実際には、この答えを聞いたあと、Aの釈放される確率はいくらになるか。 ---市川 伸一, 下條 信輔. (2010).
3囚人問題は、1959年に、Scientific American 誌の Martin Gardner のコラム "Mathematical Games" で取り上げられている。
(Gardner, Martin (1959a).;Gardner, Martin (1959b).)
モンティ・ホール問題に比べて、3囚人問題の人気は薄い。
2010年10月24日現在、Wikipediaの記事数(言語数)
| モンティ・ホール問題 | 3囚人問題 |
|---|---|
| 28ヶ国語 | 5ヶ国語 |
なお、3囚人問題の問題文をよく読むと不思議なことがわかる。「BとCのうち少なくとも1人処刑されるのは確実なのだから、 2人の中で処刑される1人の名前を教えてくれても私についての情報を与えることにはならないだろう。1人を教えてくれないか」 と囚人Aが頼むくだりでは、囚人Aが数学の確率概念の事象の独立性に着目した文になっている。 しかし 「これで自分の助かる確率は1/3から1/2に増えた」 と喜んだくだりでは一転して囚人Aが日常的な確率概念で錯覚を始めている。不思議な問題文である。
「3囚人問題」以外の3囚人問題の名称
「3囚人問題」以外の名称を見かけることはまれであるがまったく無いわけではない。
理論生物学者の個人的体験に基づいているらしい名称
サーべロニ問題 (The Serbelloni problem)
1965年から 1968年に掛けての各年に、 北イタリアにあるロックフェラー財団のベッラージオ・センター(通称 "Villa Serbelloni") で理論生物学の学術会議が催された。そのうちの 1966年の会議が 「難破」 しそうになるほどの激論になったことにちなんで、 John Maynard Smithが提案した呼び名である。 Smith, John Maynard (1968).
John Maynard Smith本人も 1965年から 1968年のいずれかの年に参加しているが、彼本人の発表でのできごとだったのか、私にはわからない。
インターネットで検索すると、「3囚人問題はサーベロニ問題という呼び名で古くから知られていた問題である」 と述べている記事を見かけるので、 さらに詳しく検索すると、 この呼称だけを使って 3囚人問題を論じている記事も僅かながら出てくる。(2012年11月現在)
John Maynard Smith本人も 1965年から 1968年のいずれかの年に参加しているが、彼本人の発表でのできごとだったのか、私にはわからない。
インターネットで検索すると、「3囚人問題はサーベロニ問題という呼び名で古くから知られていた問題である」 と述べている記事を見かけるので、 さらに詳しく検索すると、 この呼称だけを使って 3囚人問題を論じている記事も僅かながら出てくる。
3囚人問題とモンティ・ホール問題の典型的な問題文の標準仮定の明確さ比較
|
標準仮定 (3囚人問題に当てはめる場合、適宜読み替えて欲しい) |
モンティ・ホール問題の "Ask Marilyn"の問題文 |
|
3囚人問題の 市川伸一による問題文 |
|---|---|---|---|
|
① |
あいまい | = | あいまい |
|
② ホストは挑戦者の選んだ扉を開けないこと |
|
< | 明確 |
|
③ ホストは必ず残りの扉を一枚開けること |
記述なし | = | 記述なし |
|
④ ホストはハズレの扉しか開けないこと |
ほぼ明確 | < | 明確 |
|
⑤ ホストは挑戦者の選んだ扉が当たりのとき、ハズレ扉をランダムかつ等確率に選んで開けること |
記述なし | = | 記述なし |
|
⑥ ホストは扉を開けた後に必ずswitchの機会を挑戦者に与えること |
あいまい |
|
|
ちまたでの人気の割りには数学教育ではさほど重視されていない
2011年2月にある書店で調べたところ、次のようであった。
モンティ・ホール問題を例題として取り上げている統計数学の教科書は見当たらなかった。条件付確率や事後確率の例題を多数のせていながら、その中にモンティ・ホール問題も3囚人問題も含まれていないものもあった。ベイズ理論専門の教科書でやっと、3囚人問題を例題として取り上げているものがあった。そもそも条件付確率や事後確率の章を設けていない統計数学の教科書まであった。
このように、日本の統計数学の教科書ではモンティ・ホール問題や3囚人問題を例題として使っているものが少ない。
21世紀になっても、理科系の大学の卒業生に、モンティ・ホール問題や3囚人問題を解けない者がいそうである。
モンティ・ホール問題を例題として取り上げている統計数学の教科書は見当たらなかった。条件付確率や事後確率の例題を多数のせていながら、その中にモンティ・ホール問題も3囚人問題も含まれていないものもあった。ベイズ理論専門の教科書でやっと、3囚人問題を例題として取り上げているものがあった。そもそも条件付確率や事後確率の章を設けていない統計数学の教科書まであった。
このように、日本の統計数学の教科書ではモンティ・ホール問題や3囚人問題を例題として使っているものが少ない。
21世紀になっても、理科系の大学の卒業生に、モンティ・ホール問題や3囚人問題を解けない者がいそうである。
以下、この資料では、モンティ・ホール問題を話題にするとき、なるべく"Ask Marilyn"の問題文に倣うこととする
①挑戦者が選ぶものは「扉」である。(「箱」やその他のものではない)
②挑戦者は「扉1」を選んだ。
③ホストは「扉3」を開けた。
②挑戦者は「扉1」を選んだ。
③ホストは「扉3」を開けた。
以下、この資料では、3囚人問題を話題にするとき、なるべく市川 伸一, 下條 信輔. (2010).の問題文に倣うこととする
①看守に質問した囚人は囚人Aである。
②看守は囚人Bが処刑されることを囚人Aに教えた。
ただし、モンティ・ホール問題と並べて論じるときには、囚人Cが処刑されることを囚人Aに教えたことにすることもある。
②看守は囚人Bが処刑されることを囚人Aに教えた。
ただし、モンティ・ホール問題と並べて論じるときには、囚人Cが処刑されることを囚人Aに教えたことにすることもある。
モンティ・ホール問題や3囚人問題の数学的解法の概説
モンティ・ホール問題を例に挙げて、標準仮定の下での数学的解法のうち、基本的な方法をご紹介する。
方法1 : 素事象の確率を求めてから各種の事後確率を計算する方法
この方法は、Wikipedia(日本語版)の「モンティ・ホール問題」の記事に書かれている方法で、 同記事の 2003年7月14日 (月) 15:06 の版でこれを投稿した Mizusumashi さんにちなんで、 「ミズスマシ法」と私は呼んでいる。
この記念すべき「ミズスマシ法」の肝である図表と解説文は 2012年4月22日 (日) 19:42.の版にも受け継がれているが、その解説文のすぐ後に別の解説文が続いているため、読みづらくなっている。
その図表は統計数学で使う「集計表」の升目を確率で埋めたものに他ならないので、統計数学者には馴染み深いかも知れない。
数学では確率を次のように定義している。
何かの集合を標本空間として、そのべき集合の一部で加算加法族になっているものを事象の集合とし、事象の集合に確率測度を与え、・・・・・・、(難しいので以下省略)
もっと直感的な定義もある。
確率変数の値域のデカルト積のべき集合の・・・・・、(難しいので以下省略)
確率変数の値域の直積の要素に対応する事象、すなわち素事象 (prime events) を考えれば、このような数学の確率の定義に添いながら、条件付確率もしくは事後確率の計算ができるだろう。
モンティ・ホール問題でやってみると次のようになる。
例によって、挑戦者が選ぶ扉を扉1に限定して考える。
この記念すべき「ミズスマシ法」の肝である図表と解説文は 2012年4月22日 (日) 19:42.の版にも受け継がれているが、その解説文のすぐ後に別の解説文が続いているため、読みづらくなっている。
その図表は統計数学で使う「集計表」の升目を確率で埋めたものに他ならないので、統計数学者には馴染み深いかも知れない。
数学では確率を次のように定義している。
何かの集合を標本空間として、そのべき集合の一部で加算加法族になっているものを事象の集合とし、事象の集合に確率測度を与え、・・・・・・、(難しいので以下省略)
もっと直感的な定義もある。
確率変数の値域のデカルト積のべき集合の・・・・・、(難しいので以下省略)
確率変数の値域の直積の要素に対応する事象、すなわち素事象 (prime events) を考えれば、このような数学の確率の定義に添いながら、条件付確率もしくは事後確率の計算ができるだろう。
モンティ・ホール問題でやってみると次のようになる。
例によって、挑戦者が選ぶ扉を扉1に限定して考える。
ステップ1 素事象の確率の決定
確率変数の値域を確認する
「当たり扉の配置」という確率変数の値域 = { 当扉1, 当扉2, 当扉3 }
「ホストが開けた扉」という確率変数の値域 = { 開扉1, 開扉2, 開扉3, 開けない }
「ホストが開けた扉」という確率変数の値域 = { 開扉1, 開扉2, 開扉3, 開けない }
素事象に関係する連立方程式を確認する
当たり扉の配置は等確率であるので、 p(当扉1, 開扉1) + p(当扉1, 開扉2) + p(当扉1, 開扉3) + p(当扉1, 開けない) = 1/3 p(当扉2, 開扉1) + p(当扉2, 開扉2) + p(当扉2, 開扉3) + p(当扉2, 開けない) = 1/3 p(当扉3, 開扉1) + p(当扉3, 開扉2) + p(当扉3, 開扉3) + p(当扉3, 開けない) = 1/3 ホストは挑戦者が選んだ扉を開けないので、 p(当扉1, 開扉1) = 0, p(当扉2, 開扉1) = 0, p(当扉3, 開扉1) = 0 ホストは当たり扉を開けないので p(当扉1, 開扉1) = 0, p(当扉2, 開扉2) = 0, p(当扉3, 開扉3) = 0 ホストが開ける扉に偏りがないので、 p(当扉1, 開扉2) = p(当扉1, 開扉3) ホストは必ず開けるので p(当扉1, 開けない) = p(当扉2, 開けない) = p(当扉3, 開けない) = 0 確率の総和は1なので、 p(当扉1, 開扉1) + p(当扉1, 開扉2) + p(当扉1, 開扉3) + p(当扉1, 開けない) + p(当扉2, 開扉1) + p(当扉2, 開扉2) + p(当扉2, 開扉3) + p(当扉2, 開けない) + p(当扉3, 開扉1) + p(当扉3, 開扉2) + p(当扉3, 開扉3) + p(当扉3, 開けない) = 1
方程式を解いて求めた確率をテーブルに配置する
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉1 | 当扉1, 開扉1 0 | 当扉2, 開扉1 0 | 当扉3, 開扉1 0 |
| 開扉2 | 当扉1, 開扉2 1/6 | 当扉2, 開扉2 0 | 当扉3, 開扉2 1/3 |
| 開扉3 | 当扉1, 開扉3 1/6 | 当扉2, 開扉3 1/3 | 当扉3, 開扉3 0 |
| 開けない | 当扉1, 開けない 0 | 当扉2, 開けない 0 | 当扉3, 開けない 0 |
ホストが必ずどれかの扉を開けることを前提とする場合には、下のように、ホストが扉を開けないケースを最初から含めないことになる。
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉1 | 当扉1, 開扉1 0 |
当扉2, 開扉1 0 |
当扉3, 開扉1 0 |
| 開扉2 | 当扉1, 開扉2 1/6 |
当扉2, 開扉2 0 |
当扉3, 開扉2 1/3 |
| 開扉3 | 当扉1, 開扉3 1/6 |
当扉2, 開扉3 1/3 |
当扉3, 開扉3 0 |
ステップ2 事後確率の計算
「扉1が当たり」という事象を仮説事象とし、「ホストがハズレの扉3を開いた」という事象を証拠事象とする場合
ホストがハズレの扉3を開いたという証拠事象の範囲だけ切り出す
確率の比率を変えずに、総和が1になるように調整する
扉1から扉2にswitchして賞品を得るということは、扉2が当たりであるということである。上で得た図によると、その確率は 2/3 である。
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉3 | 当扉1, 開扉3 1/6 |
当扉2, 開扉3 1/3 |
確率の比率を変えずに、総和が1になるように調整する
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉3 | 当扉1, 開扉3 1/3 |
当扉2, 開扉3 2/3 |
扉1から扉2にswitchして賞品を得るということは、扉2が当たりであるということである。上で得た図によると、その確率は 2/3 である。
「扉1が当たり」という事象を仮説事象とし、「ホストがハズレの扉2またはハズレの扉3を開いた」という事象を証拠事象とする場合
ホストがハズレの扉2 あるいはハズレの扉3 を開いたという証拠事象の範囲だけ切り出す
確率の比率を変えずに、総和が1になるように調整する
扉1から switchして賞品を得るということは、扉2 または扉3 が当たりであるということである。上で得た図によると、その確率は 2/3 である。
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉2 | 当扉1, 開扉2 1/6 |
当扉3, 開扉2 1/3 |
|
| 開扉3 | 当扉1, 開扉3 1/6 |
当扉2, 開扉3 1/3 |
確率の比率を変えずに、総和が1になるように調整する
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉2 | 当扉1, 開扉2 1/6 |
当扉3, 開扉2 1/3 |
|
| 開扉3 | 当扉1, 開扉3 1/6 |
当扉2, 開扉3 1/3 |
扉1から switchして賞品を得るということは、扉2 または扉3 が当たりであるということである。上で得た図によると、その確率は 2/3 である。
補足
Wikipedia(日本語版)の「モンティ・ホール問題」の記事の「計算」の項(2011/12/06現在)を除くと、上記のような図表を使ってモンティ・ホール問題を考える人は多くないが、インターネット上では次のような例がある。
・TETRAさんのブログ 「モンティ・ホール問題(確率) | TETRA'S MATH」 の 「モンティ・ホール問題・03」 の段に同様の図が使われている。
・TETRAさんのブログ 「モンティ・ホール問題(確率) | TETRA'S MATH」 の 「モンティ・ホール問題・03」 の段に同様の図が使われている。
素事象の確率を求めてから各種の事後確率を計算する方法を「戦略に着目した問題設定」に適用した場合
この問題設定には、①条件付確率や事後確率を計算しない、②ホストが扉を開けない場合も計算に含める、という特徴がある。
まず、条件を整理する。
まず、条件を整理する。
・挑戦者は扉1を選ぶjものとする。
・ホストは扉を開けないことがある。(開けない確率を p とする)
・扉を開けない確率は、どの扉が当たりでも変わらないとする。
・ホストは当たりの扉を開けない。
・ホストは挑戦者の選んだ扉を開けない。
・開けたら必ずswitchの機会が与えられる。
この条件で標本空間を図示すると次のようになる。
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉1 | 当扉1, 開扉1 0 |
当扉2, 開扉1 0 |
当扉3, 開扉1 0 |
| 開扉2 | 当扉1, 開扉2 ( 1 - p) / 6 |
当扉2, 開扉2 0 |
当扉3, 開扉2 ( 1 - p) / 3 |
| 開扉3 | 当扉1, 開扉3 ( 1 - p) / 6 |
当扉2, 開扉3 ( 1 - p) / 3 |
当扉3, 開扉3 0 |
| 開けない | 当扉1, 開けない p / 3 |
当扉2, 開けない p / 3 |
当扉3, 開けない p / 3 |
ここから、switch の機会が与えられたら必ず switch する戦略で賞品を得るケースを抜き出すと下図のようになる。
| 当扉1 | 当扉2 | 当扉3 | |
| 開扉2 | 当扉3, 開扉2 ( 1 - p) / 3 |
||
| 開扉3 | 当扉2, 開扉3 ( 1 - p) / 3 |
||
| 開けない | 当扉1, 開けない p / 3 |
この表から、「switch の機会が与えられたら必ず switch する戦略」で賞品を得るケースの総確率は
( ( 1 - p ) + ( 1 - p ) + p ) / 3 = 2/3 - p/3 となる。
標準仮定が成立する場合は p = 0 なので 2/3 となり、非条件付確率の問題設定の場合と一致する。
方法2 : 標本空間の図を使わず、条件付確率の定義だけを使って計算する方法
(2011/11/11 に全面的に画き直しました)
ベイズ推定で使う公式を用いて計算する方法との大きな違いは、計算式に尤度 (仮説事象を条件とする証拠事象の条件付確率) が目立つ形で出てこない点にある。
モンティ・ホール問題を題材として、挑戦者が選んだ扉を扉1に限定した 特定事象による条件付確率あるいは事後確率の解答 を例とした場合、次のようになる。
ベイズ推定で使う公式を用いて計算する方法との大きな違いは、計算式に尤度 (仮説事象を条件とする証拠事象の条件付確率) が目立つ形で出てこない点にある。
モンティ・ホール問題を題材として、挑戦者が選んだ扉を扉1に限定した 特定事象による条件付確率あるいは事後確率の解答 を例とした場合、次のようになる。
| 個別事象に着目した場合 | 余事象に着目した場合 | |
|---|---|---|
|
|
扉2が当り | 扉2か扉3が当り |
| 証拠事象 | ホストが扉3を開ける | ホストが扉3を開ける |
| 計算 |
仮説事象と証拠事象が同時成立する確率= 扉2が当りでホストが扉3を開ける確率= 1 / 3 証拠事象の確率= ホストが扉3を開ける確率= 1 / 2 目的の条件付確率= 2 / 3 注:証拠事象の確率は、当り扉や開ける扉の対象性によって直接導いています。 ・・・そうしないとベイズ推定で使う公式との違いが薄くなる |
仮説事象と証拠事象が同時成立する確率= 扉1がハズレでホストが扉3を開ける確率= (2 / 3) × (1 / 2) = 1 / 3 証拠事象の確率= ホストが扉3を開ける確率= 1 / 2 目的の条件付確率= 2 / 3 注:証拠事象の確率は、当り扉や開ける扉の対象性によって直接導いています。 ・・・そうしないとベイズ推定で使う公式との違いが薄くなる |
方法3 : ベイズ推定で使う公式を用いて計算する方法
(2011/11/11 に全面的に画き直しました)
条件付確率の定義だけを使って計算する方法との大きな違いは、計算式に尤度 (仮説事象を条件とする証拠事象の条件付確率) が目立つ形で出て来る点にある。
モンティ・ホール問題を題材として、挑戦者が選んだ扉を扉1に限定した 特定事象による条件付確率あるいは事後確率の解答 を例とした場合、次のようになる。
条件付確率の定義だけを使って計算する方法との大きな違いは、計算式に尤度 (仮説事象を条件とする証拠事象の条件付確率) が目立つ形で出て来る点にある。
モンティ・ホール問題を題材として、挑戦者が選んだ扉を扉1に限定した 特定事象による条件付確率あるいは事後確率の解答 を例とした場合、次のようになる。
| 個別事象に着目した場合 | 余事象に着目した場合 | |
|---|---|---|
|
|
扉1が当り | 扉1が当り |
| 仮説事象② | 扉2が当り | 扉2か扉3が当り |
| 証拠事象 | ホストが扉3を開ける | ホストが扉3を開ける |
| 計算 |
仮説事象①の尤度 = 扉1が当りのときにホストが扉3を開ける確率 = 1 / 2 仮説事象②の尤度 = 扉2が当りのときにホストが扉3を開ける確率 = 1 証拠事象の確率 = (1 / 2)(1 / 3) + 1 / 3 = 1 / 2 仮説事象②と証拠事象が同時成立する確率 = 仮説事象②の尤度× 仮説事象②の確率 = 1 / 3 証拠事象の下での仮説事象②の条件付確率 = (1 / 3) / (1 / 2) = 2 / 3 |
仮説事象①の尤度 = 扉1が当りのときにホストが扉3を開ける確率 = 1 / 2 仮説事象②の尤度 = 扉2か扉3が当りのときにホストが扉3を開ける確率 = 1 / 2 証拠事象の確率 = (1 / 2)(1 / 3) + (1 / 2)(2 / 3) = 1 / 2 仮説事象②と証拠事象が同時成立する確率 = 仮説事象②の尤度× 仮説事象②の確率 = 1 / 3 証拠事象の下での仮説事象②の条件付確率 = (1 / 3) / (1 / 2) = 2 / 3 |
方法4 : 架空の統計データを想像して計算する方法
架空の統計データを想像して解く方法ならば、「条件付確率あるいは事後確率の問題」を、「標本空間」などの確率論の知識なしに解くことができるので、小学生にも教えやすい。
「特定事象による条件付確率あるいは事後確率の解答」について、モンティ・ホール問題を題材に、挑戦者が扉1を選び、ホストが扉3を開けた場合を例に説明する。
「特定事象による条件付確率あるいは事後確率の解答」について、モンティ・ホール問題を題材に、挑戦者が扉1を選び、ホストが扉3を開けた場合を例に説明する。
| 過去に18万回ゲームを行って、18万件のデータがとれたとする。 |
| ↓ |
| 当たり扉の設定がランダムかつ等確率の場合 18万件のデータのうち、扉1が当たりであるデータも、 扉2が当たりであるデータも約6万件ずつである。 |
| ↓ |
| 挑戦者による扉の選択がランダムかつ等確率だとした場合 扉1が当たりで挑戦者が扉1を選択したデータも、 扉2が当たりで挑戦者が扉1を選択したデータも約2万件ずつである。 |
| ↓ |
| 挑戦者が選択しなかった扉2と扉3が両方ともハズレのとき、
ホストがランダムかつ等確率にどちらを開けるか決める場合 扉1が当たりで挑戦者が扉1を選択したときにホストtが扉3を開けたデータは約1万件であるが、 扉2が当たりで挑戦者が扉1を選択したときにホストが扉3を開けたデータは約2万件である。 |
| ↓ |
| 「挑戦者が扉1を選びホストが扉3を開けた」データの中で、 扉1が当たりのデータが約1万件、扉2が当たりのデータが約2万件あることになる。 |
| ↓ |
| 挑戦者が扉1を選びホストが扉3を開いた時点で 扉2が当たりである確率、すなわち switch して賞品を獲得する確率は 2万/(1万 + 2万)、すなわち 2/3 である。 |
方法5 : ベイズ推定の公式を忘れた人のための「標本空間の時系列的階層分割」
標本空間を時系列的階層分割すれば自ずと「条件付確率あるいは事後確率の解答」を求めることができ、しかも計算内容がベイズ推定の公式とまったく変わらないので、ベイズの定理やベイズ推定の公式を覚える必要はない。
一般的には、下図のような斜めの線を使った樹形図を使うことが多い。
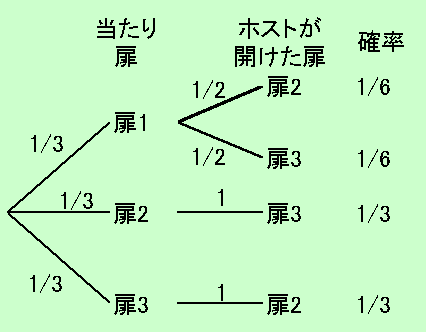
しかし、ここでは以下に示すように斜めの線を使わずに Excel で簡単に書ける方法をご紹介する。
この方法の手順は次のとおりである。
一般的には、下図のような斜めの線を使った樹形図を使うことが多い。
しかし、ここでは以下に示すように斜めの線を使わずに Excel で簡単に書ける方法をご紹介する。
この方法の手順は次のとおりである。
- ①標本空間の時系列的階層分割を行う
- ②挑戦者が扉1を選びホストがハズレの扉3を開けるという条件に当てはまる事象ごとの事前確率を求める
- ③事前確率を確からしさと見なし、それらを総合して条件付確率あるいは事後確率を計算する
モンティ・ホール問題を題材として実際にやってみる。
簡単のため、挑戦者が扉1を選んだケースのみを考えることとし(当たり扉の設定がランダムであれば一般性を失わない)、挑戦者が扉を選んだ後の標本空間で議論することとする。
A)挑戦者が選んだ扉が当たりの事象と、その余事象に着目した場合の計算手順
ホストが扉3を開いた場合を考える。
ホストが開ける扉の確率がすべて1/2であることに着目
| どの扉が当たりか (数字はその事象の確率) | 扉1 ( 1 / 3 ) |
扉1以外 ( 2 / 3 ) |
||
| ホストが開ける扉 (数字は上を条件とした確率) | 扉2 ( 1 / 2 ) |
扉3 ( 1 / 2 ) |
扉3 ( 1 / 2 ) |
扉2 ( 1 / 2 ) |
| 事前確率 あるいは確からしさ | 1 / 6 = (1 / 3)×(1 / 2) |
1 / 3 = (2 / 3)×(1 / 2) |
||
| 確からしさの総和 | 1 / 2 = ( 1 / 6 ) + ( 1 / 3 ) | |||
| 条件付確率 あるいは事後確率 | 1 / 3 = (1 / 6) / (1 / 2) |
2 / 3 = (1 / 3) / (1 / 2) |
||
ホストが開ける扉の確率がすべて1/2であることに着目
B)3つの扉それぞれが当たりの事象に着目した場合の計算手順
ホストが扉3を開いた場合を考える。
ホストが開ける扉の確率に 1/2 と 1 が混在していることに着目
| どの扉が当たりか (数字はその事象の確率) | 扉1 ( 1 / 3 ) |
扉2 ( 1 / 3 ) |
扉3 ( 1 / 3 ) |
|
| ホストが開ける扉 (数字は上を条件とした確率) | 扉2 1 / 2 |
扉3 1 / 2 |
扉3 1 |
扉2 1 |
| 事前確率 あるいは確からしさ | 1 / 6 = (1 / 3)×(1 / 2) |
1 / 3 = (1 / 3)×1 |
||
| 確からしさの総和 | 1 / 2 = ( 1 / 6 ) + ( 1 / 3 ) | |||
| 条件付確率 あるいは事後確率 | 1 / 3 = (1 / 6) / (1 / 2) |
2 / 3 = (1 / 3) / (1 / 2) |
||
ホストが開ける扉の確率に 1/2 と 1 が混在していることに着目
「特定事象による条件付確率あるいは事後確率の解答」と「非条件付確率の解答」の関係の特殊例
標準仮定の「①当たり扉はランダムかつ等確率に設定される」が成立していなくても、同時に「等確率開扉の仮定」も成立しないのであれば、「特定事象による条件付確率あるいは事後確率の問題設定」と「非条件付確率の解答」が一致することがある。
例えば、「挑戦者が選んだ扉1が当たりのときにホストが残りの扉2を開ける確率と扉3を開ける確率の比が、扉2がハズレの確率と扉3がハズレの確率の比に等しい」という関係があるならば、「特定事象による条件付確率あるいは事後確率の解答」と「非条件付確率の解答」が一致する。
上記の議論は3囚人問題でも同様に成立する。
例えば、「挑戦者が選んだ扉1が当たりのときにホストが残りの扉2を開ける確率と扉3を開ける確率の比が、扉2がハズレの確率と扉3がハズレの確率の比に等しい」という関係があるならば、「特定事象による条件付確率あるいは事後確率の解答」と「非条件付確率の解答」が一致する。
上記の議論は3囚人問題でも同様に成立する。
「不特定事象による条件付確率あるいは事後確率の解答」と「戦略に着目した解答」の関係
標準仮定の下では、「不特定事象による条件付確率あるいは事後確率の問題設定 」での解答と「戦略に着目した問題設定」での解答は本質的に一致する。
しかし、標準仮定の中の、「③ホストは必ず残りの扉を一枚開ける」という仮定と、「⑥ホストは扉を開けた後に必ずswitchの機会を挑戦者に与える」という仮定が成立しない場合は、このように一致するとは限らない。
例えば、挑戦者が当たりを選んだら100%の確率でswitchの権利を与え、ハズレを選んだら50%の確率でswitch の権利を与えるといった条件(この条件を「半分だけ地獄から来たモンティ」と呼びたい) の場合、「戦略に着目した解答」ではswitchするという戦略で賞品を得る確率は 1/3 であるが、「不特定事象による条件付確率あるいは事後確率の解答」では、switchしたときに賞品を得る確率は 1/2 となる。
上記の議論は3囚人問題でも同様に成立する。
しかし、標準仮定の中の、「③ホストは必ず残りの扉を一枚開ける」という仮定と、「⑥ホストは扉を開けた後に必ずswitchの機会を挑戦者に与える」という仮定が成立しない場合は、このように一致するとは限らない。
例えば、挑戦者が当たりを選んだら100%の確率でswitchの権利を与え、ハズレを選んだら50%の確率でswitch の権利を与えるといった条件(この条件を「半分だけ地獄から来たモンティ」と呼びたい) の場合、「戦略に着目した解答」ではswitchするという戦略で賞品を得る確率は 1/3 であるが、「不特定事象による条件付確率あるいは事後確率の解答」では、switchしたときに賞品を得る確率は 1/2 となる。
上記の議論は3囚人問題でも同様に成立する。
標準仮定の下で、「特定事象による条件付確率あるいは事後確率の解答」と「非条件付確率の解答」が一致することの説明
①ベイズ推定の公式を使った計算を逆にたどる方法
標準仮定のもとでは囚人や扉の間の対称性により、証拠事象によらず全ての事後確率が同じ値になる。また、標準仮定の下では仮説事象が成立した場合に必ず証拠事象が成立するので、事後確率の証拠事象の確率による加重平均が事前確率に一致する。これらにより、事後確率と事前確率も同じ値になるので、事後確率を求める「特定事象による条件付確率あるいは事後確率の問題設定」と事前確率を求める「非条件付確率の問題設定」での解答が一致することが導かれる。
②扉の間の対象性から導かれる証拠事象と仮説事象の独立性を利用する方法
モンティ・ホール問題に対して、Richard Gill が2011年2月に対称性に基づく解法を提案し、Wikipedia(英語版)の"Monty Hall Problem"の記事に"Proof using a simple solution and symmetry." の項目として採用された。
この項目の既述は私には難解で余り自信が無いが、標準仮定の下で switchして賞品を得る事象の事前確率とホストが特定の扉を開けた後の事後確率が一致することを、次のような論法で証明しているようだ。
この項目の既述は私には難解で余り自信が無いが、標準仮定の下で switchして賞品を得る事象の事前確率とホストが特定の扉を開けた後の事後確率が一致することを、次のような論法で証明しているようだ。
3つの扉の間の対称性に着目すると、ホストが扉3を開ける確率が挑戦者が選んだ扉1の当たりハズレに関係しないことがわかる。 したがって、ホストが扉3を開けるか否かという事象が、挑戦者が選んだ扉が当たりかハズレかという事象と統計的に独立である。 その結果、ホストが扉3を開けたという証拠事象の考慮が不要になるので、 switchして賞品を得る事象の事前確率と事後確率が一致する。
③選んだ扉が当たりの可能性とハズレの可能性の比が変わらないことを利用する方法
当たり扉と選んだ扉の組み合わせごとの可能性が均一なので、扉を選ぶ前と後で、選んだ扉が当たり の可能性と選んだ扉がハズレの確からしさの比は、選んだ扉が確定しても 変わらない。
ホストが扉を開けたとき、ホストがもう一つの扉を開ける分が減ったため、ホストが開け方に偏りがなければ、選んだ扉が当たりの可能性選んだ扉がハズレの可能性が、両方とも半分になり、開けた扉が確定しても それらの比は変わらない。
したがって、switchして賞品を得る事象、すなわち、選んだ扉がハズレである事象の、 選んだ扉と開けた扉 を証拠事象とする事後確率は事前確率と一致する。
ホストが扉を開けたとき、ホストがもう一つの扉を開ける分が減ったため、ホストが開け方に偏りがなければ、選んだ扉が当たりの可能性選んだ扉がハズレの可能性が、両方とも半分になり、開けた扉が確定しても それらの比は変わらない。
したがって、switchして賞品を得る事象、すなわち、選んだ扉がハズレである事象の、 選んだ扉と開けた扉 を証拠事象とする事後確率は事前確率と一致する。
「特定事象による条件付確率あるいは事後確率の解答」、「不特定事象による条件付確率あるいは事後確率の解答」、「非条件付確率の解答」、および「戦略に着目した解答」の結果比較
◇ Wikipedia(英語版)の"Monty Hall problem"の記事(2010年8月8日現在)に書かれていた変形問題を題材に、これらの解答の結果を比較してみる。
※変形問題のニックネームについては、Wikipedia(英語版)の"Monty Hall problem"の記事(2010年8月8日現在)を参考にしたものと、オリジナルなものの2種類ある。
| 変形問題のニックネーム |
変形問題における ホストの行動 |
特定事象による条件付確率あるいは事後確率の解答 ホストが残した扉にswitchすると賞品を得る確率 |
不特定事象による条件付確率あるいは事後確率の解答 ホストが残した扉にswitchすると賞品を得る確率 |
非条件付確率の解答 ホストが残した扉にswitchすると賞品を得る確率 |
戦略に着目した解答 switch 戦略で賞品を得る確率 |
|---|---|---|---|---|---|
|
地獄から 来た モンティ |
挑戦者が当たりの扉を選らんだとき、かつそのときだけ switchの選択権を与える。 (Tierney, John (1991).) | 0 | 0 | ホストが扉を開くとは限らないため、問題設定が成り立たない。 | 0 |
|
天使 モンティ |
挑戦者がハズレの扉を選んだとき、かつそのときだけswitchの選択権を与える。(Granberg, Donald (1996). ) | 1 | 1 | ホストが扉を開くとは限らないため、問題設定が成り立たない。 | 1 |
|
偏った モンティ |
ホストは必ずハズレの扉を開けてswitchの権利を与える。ホストが2枚の扉を開けることができるとき、若番の扉を確率 p で、老番の扉を確率 q = 1 - p であける。(p = q = 1/2 が標準型モンティ・ホール問題のケース) (Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). ) (Rosenthal, Jeffrey S. (2005b)) |
挑戦者が扉1を選らび、ホストが扉3を開けた場合、 1/(1+ q) |
2/3 | 2/3 | 2/3 |
|
無知な モンティ |
ホストはどの扉に何があるか知らないで、挑戦者が選ばなかった扉のうち1枚をランダムに開ける。 (Granberg, Donald and Brown, Thad A. (1995). ) (Rosenthal, Jeffrey S. (2005a). ;Rosenthal, Jeffrey S. (2005b)) |
1/2 | 1/2 | ホストがハズレの扉を開くとは限らないため、問題設定が成り立たない。 |
1/3 (ゲームが流れるケースを含んだ値) |
|
計画的 モンティ |
ホストは挑戦者が選ぶ前に、どのハズレの扉を開けるか決める。挑戦者がその扉を選ばなかったときだけ、その扉を開ける。 | 1/2 | 1/2 | ホストが扉を開くとは限らないため、問題設定が成り立たない。 |
1/3 (ゲームが流れるケースを含んだ値) |
|
半分だけ地獄から来た モンティ |
挑戦者が当たりを選んだら100%の確率でswitchの権利を与え、ハズレを選んだら50%の確率でswitch の権利を与える。 (Mueser, Peter R. and Granberg, Donald (May 1999). の "APPENDIX A:" に書かれている) |
1/2 | 1/2 | ホストが扉を開くとは限らないため、問題設定が成り立たない。 |
1/3 (switchの権利が与えられないケースを含んだ値) |
※試しに上の表の「偏ったモンティ」と「無知なモンティ」を組み合わせてみると、「無知なモンティ」の場合と同じ結果になった。つまり、無知なモンティが開ける扉に選り好みがあっても確率に影響しない。
特定事象による条件付確率あるいは事後確率の問題設定の理解を助ける表象
特定事象による条件付確率あるいは事後確率の問題設定に対する理解を助けるような表象(図式表現)がいくつか考案されている。
◇ ルーレット表現
特定事象による条件付確率あるいは事後確率の問題設定を説明する最も簡単な図が、市川伸一のルーレット表現である。扇形の角度の大小が確からしさの大小と対応している。モンティ・ホール問題にルーレット表現を適用すると次のようになる。
注1) モンティ・ホール問題で挑戦者が扉1を選んだ場合に限定した標本空間を表している。
注2) 証拠事象(ホストが扉3を開けること)に含まれていない部分を灰色で示した。
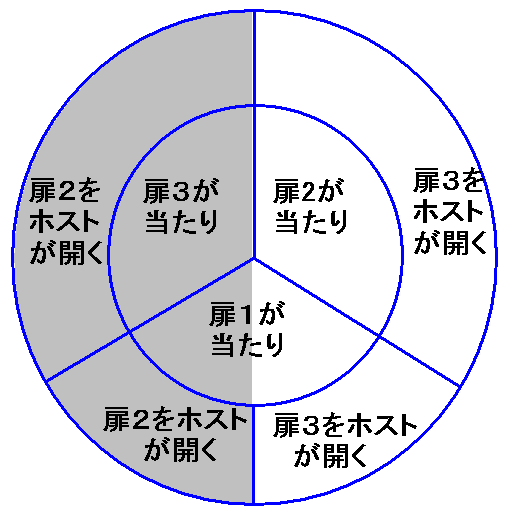
注1) モンティ・ホール問題で挑戦者が扉1を選んだ場合に限定した標本空間を表している。
注2) 証拠事象(ホストが扉3を開けること)に含まれていない部分を灰色で示した。
◇ 確からしさを横幅で表しながら標本空間の階層構造を四角形の積み重ねで表現する方法
Wikipedia(英語版)の"Monty Hall problem"の記事で事後確率の計算方法を説明する図でこの方法が使われている。(2010年8月8日現在)
Wikipedia(英語版)の図のイラストを省くなどして簡略化すると次のようになる。
各マスの横幅の大小が確からしさの大小と対応している。
この図は市川のルーレット表現の図を切り開いて展開した図と見ることができる。
理解しやすさの点で市川のルーレット表現より劣っているかわりに Excel で書きやすい。
Wikipedia(英語版)の図は、ヤギや自動車のイラスト入りで楽しい。
縦に積むのでなく、横向きに並べて書いた例を、Wikipedia(ロシア語版)の"Парадокс Монти Холла"の記事で、2005年7月24日 00:16 の版から 2005年11月10日15:33 の版に掛けて見ることができた。
四角の高さの大小が確からしさの大小に対応している。
この図は 2005年12月2日 12:57 の版で削除されていた。
Wikipedia(英語版)の図のイラストを省くなどして簡略化すると次のようになる。
各マスの横幅の大小が確からしさの大小と対応している。
| 扉3が 当たり | 扉1が 当たり | 扉2が 当たり | |
| 扉1を 選択 | 扉1を 選択 | 扉1を 選択 | |
| 扉2を ホストが 開く | 扉2を ホストが 開く | 扉3を ホストが 開く | 扉3を ホストが 開く |
| ホストが扉2を開けたならswitchして獲得する確率はStayして獲得する確率の2倍 | ホストが扉3を開けたならswitchして獲得する確率はStayして獲得する確率の2倍 | ||
この図は市川のルーレット表現の図を切り開いて展開した図と見ることができる。
理解しやすさの点で市川のルーレット表現より劣っているかわりに Excel で書きやすい。
Wikipedia(英語版)の図は、ヤギや自動車のイラスト入りで楽しい。
縦に積むのでなく、横向きに並べて書いた例を、Wikipedia(ロシア語版)の"Парадокс Монти Холла"の記事で、2005年7月24日 00:16 の版から 2005年11月10日15:33 の版に掛けて見ることができた。
四角の高さの大小が確からしさの大小に対応している。
| Door Object Is Behind | Door Initialy Chosen | Door Revealed |
| A | A | B |
| C | ||
| B | C | |
| C | B |
この図は 2005年12月2日 12:57 の版で削除されていた。
条件付確率や事後確率の教育を受けていない人々(数学者含む)が、モンティ・ホール問題や3囚人問題を与えられたときに行う確率判断について、次のような認知心理学的課題がある。
- ①「学校で習っていないので解けない」ことに気付かずに、残った扉が2枚だからとか、残った囚人が二人だからといった素朴な確率論に頼って答えを出してしまうのは何故か、
- ②確率が 1/2 にならない理由を理解してもなお、心で納得することができないのは何故か
- ③挑戦者が選ばなかった二つの扉の中に当たりがある確率がホストが開けなかった扉に継承されるという数学的に怪しげな説明を考え出すのは何故か
参考になる人々の言動
上記の心理現象を考える上で、人々の実際の言動が参考になる。
参考1 仮説事象と証拠事象を組合せないで単純な標本空間を作ってしまった人の例
以下の二つの例で、まったく同じ論法をとっていて、次のような共通点がある。
- ホストが扉を開いた後の確率を計算しなおしているので、事後確率の最も素朴な考え方は持っているらしい。
- それでいて事後確率の計算方法を明確に意識することなく直接的に答えを出している。
- 仮説事象と証拠事象を組み合わせた標本空間を組み立ててから事後の標本空間を抽出する必要性に気付いない。
"Ask Marilyn"に反論の投書をした Sachs博士の例
1991年7月21日の New York Times 日曜版で紹介された Marilyn vos Savant に反論した博士たちの一人、Sachs博士は次のように述べている。
- ①一つの扉がハズレであることが判ったので残りの扉が当たりの確率が変化する。
- ②それらの確率が 1/2 より大きくなる理由がない。
The Straight Dope での議論
"Ask Marilyn"の問題文に対する Marllyn vos Savant の解答を疑ったMichael Griceからの投書に対して Cecil Adams が次のように解答している。
- ①扉が3つのときは当たりの扉を選ぶ確率は 1/3 である。
- ②扉の数が1つ減れば、残りの扉が当たりである確率は等しいので 1/2 になる。
参考2 非条件付確率の問題設定に思い至る人が少ないこと
「非条件付確率の問題設定」に行き着けば、統計数学の知識無しに問題を解けるにも関わらず、そのような問題設定に思い至る人は少ない。このことから、無意識に事後確率の世界に標本空間を切り替えてしまい、無意識であるがゆえに後戻りできない人が多いことがわかる。
私の体験
私も、「行動経済学 経済は「感情」で動いている」(友野典男 著) に書かれていた「非条件付確率の問題設定」での解答を理解できなくて、「特定事象による条件付確率あるいは事後確率の問題設定」での解答を自力で導いたりしていた。
「非条件付確率の問題設定」と、「特定事象による条件付確率あるいは事後確率の問題設定」が、そもそも別個の問題であることに気付いたのは、かなり時間が経った後だった。
「非条件付確率の問題設定」と、「特定事象による条件付確率あるいは事後確率の問題設定」が、そもそも別個の問題であることに気付いたのは、かなり時間が経った後だった。
非条件付確率の問題設定が条件付確率あるいは事後確率の問題設定とは別個の問題設定であることに気付ける人が少ない
インターネットのブログなどを読んでも、これに気付いている人を見たことが無い。
非条件付確率の問題設定での説明と、条件付確率あるいは事後確率の問題設定での説明が、同じ問題の「別解」だと思っている人が多い。
さすがに Wikipedia(英語版)の "Monty Hall problem"の記事はこの区別に気付いている。また、これに気付いている人の論文やコメントを統計数学の論文誌で読んだことがある。
非条件付確率の問題設定での説明と、条件付確率あるいは事後確率の問題設定での説明が、同じ問題の「別解」だと思っている人が多い。
さすがに Wikipedia(英語版)の "Monty Hall problem"の記事はこの区別に気付いている。また、これに気付いている人の論文やコメントを統計数学の論文誌で読んだことがある。
非条件付確率の問題設定を理解しても受け入れられない人がいる
問題設定別の確率値の違いを論じながら、非条件付確率の問題設定を "wrong" だと形容している統計数学の論文を見たことがある。
参考3 ホストの立場に立った説明だと納得しやすいこと
インターネットのQAサイトに質問を投稿した人の例
質問を投稿した本人が自分で数学的な説明を考えたり、二人の回答者のアンサーを読んだり、自分で実験して検証した後にも不思議さが消えなかったが、ある回答者の「出題者(ホストのこと)が答えを知っているというのがみそです」という言葉から「答えを知っている出題者が当たる確率を凝縮してくれた」という風に理解してやっと疑問が晴れた。
この例から、
この例から、
- ①数学的な説明では不思議さがなくならないこと
- ②ホストが扉を開く前後の標本空間をつなぐパイプをイメージさせてくれるような説明を求めていること
DOFIさんが作った人気のページ 「ネコでもわかるモンティホールジレンマ」 (2012年01月09日現在)
ホスト猫の側に立って、賞品の魚を隠した扉を開けないように注意しながら扉の数を2枚まで減らす実習の説得力が高い。モンティ・ホール問題と長く付き合っている私がそう感じるのだから、初心者にもわかりやすいだろう。
参考4 確率が「継承」される、といった説明をする人の例
下記の例では、挑戦者が選ばなかった二つの扉の確率が「そのまま」ホストが開けなかったた方の扉に継承されると考えている。あたかも物理学の保存則のような原理が働いているかのようである。
①経済学書に載ったモンティ・ホール問題の解説
2001年1月に出版された "Butterfly Economics: A New General Theory of Social and Economic Behavior"、Paul Ormerod 著の中で、モンティ・ホール問題を取り上げている。
インターネット上のある書評サイトに、この本の書評が載っていて、それによると、Paul Ormerod は次のように説明しているらしい。
インターネット上のある書評サイトに、この本の書評が載っていて、それによると、Paul Ormerod は次のように説明しているらしい。
- ①プレイヤーが扉Aを選らんだとき、扉BまたはCで賞品を得るオッヅは 2/3 である。
- ②扉Cが除かれたことにより、扉Bが 2/3 というチャンスを継承する。
②平成教育委員会でのモンティ・ホール問題の解説
2010年1月3日の平成教育委員会にお年玉を題材とするモンティ・ホール問題が出されて、幾通りかの説明がなされた。インターネットのあるブログによると、「たけし先生による別解」は次のようなものであったらしい。
最初の時点ではどの袋も、当たりである(お年玉が入っている)確率は等しく 1/3 です。
つまりB,Cのどちらかにお年玉が入っている確率は 2/3
親のヒントにより、Cが空だとわかった(当たりの確率が 0 になった)ため、Cにあった 1/3 の望みはBに移動し、Bの当たりの確率は 2/3 になる。
参考5 扉の枚数を桁違いに多くすると正解に納得しやすいこと
扉の数を百万枚など桁違いに増やした場合を想像させて switchした方が有利であることを納得させる方法があり、多くの人がこの説明を採用している。
- Wikipedia(英語版)の"Monty Hall problem"の記事の "Increasing the number of doors" の項目 (2010年08月08日現在)
- Wikipedia(日本語版)の「モンティ・ホール問題」の記事の「直感と理論の乖離」の項目 (2010年08月08日現在)
- Yahoo!知恵袋や、Yahoo! Answers のQAサイトでも良く見かける。
数学的に無意味な説明であるにも関わらず、この説明で納得する人が多いことから、モンティ・ホール問題や3囚人問題の不思議さの原因は数学的な理解不足でないことがわかる。
参考6 扉を並べて賞品の配置パターンを図示する説明がわかりやすいこと
次のような説明図による説明の人気が高い。
しかしこの図は次の図より情報量が増えていない。
このことは、人間が確率を考える場合に標本空間だけで確率を考えることが得意でなく、扉を並べたイメージの上でなければ確率を考えられないことを示している。
挑戦者が扉1を選んだとする。
|
しかしこの図は次の図より情報量が増えていない。
挑戦者が扉1を選んだとする。
|
このことは、人間が確率を考える場合に標本空間だけで確率を考えることが得意でなく、扉を並べたイメージの上でなければ確率を考えられないことを示している。
参考7 私が体験した「標本空間重ね合わせ現象」
条件付確率あるいは事後確率に慣れ親しんでいたとしても、次のような思考プロセスを辿りがちであることが、私自身の体験からわかった。
モンティ・ホール問題で、当たり扉の配置が等確率でない場合を考えていたとき、最初に次のような標本空間を思い浮かべてしまった。
そして、ホストが扉3を開けた後の標本空間として、次のようなものを考えてしまった。
(この表の上の数字は確からしさfr、下の数字は確率)
そして、自分がホストの行動を組み入れた標本空間を考えていないことに気付くのに、10分以上時間が掛かってしまった。
当り扉に着目した標本空間とホストが開ける扉に着目した標本空間のデカルト積で標本空間を構成しなければならないのに、単純に重ね合わせてしまったのだろう。
モンティ・ホール問題で、当たり扉の配置が等確率でない場合を考えていたとき、最初に次のような標本空間を思い浮かべてしまった。
| 当扉1 | 当扉2 | 当扉3 |
| 0.2 | 0.6 | 0.2 |
そして、ホストが扉3を開けた後の標本空間として、次のようなものを考えてしまった。
| 当扉1 | 当扉2 |
| 0.2 0.125 | 0.6 0.75 |
(この表の上の数字は確からしさfr、下の数字は確率)
そして、自分がホストの行動を組み入れた標本空間を考えていないことに気付くのに、10分以上時間が掛かってしまった。
当り扉に着目した標本空間とホストが開ける扉に着目した標本空間のデカルト積で標本空間を構成しなければならないのに、単純に重ね合わせてしまったのだろう。
参考8 扉自体の属性として確率をとらえた表現をする人がいること
英文で "door 1 has chance 1/3 of ・・・"のような言い回しを見かけたことがある。
別のある人のブログで、次のような言い回しを見たことがある。
別のある人のブログで、次のような言い回しを見たことがある。
最初に選んだ扉が当たりである確率は 1 / 3 で、残り二つのうちどちらかに当たりが入ってる確率は 2 / 3 だ。
残り二つのうちどちらかに当たりが入ってる確率は 2 / 3 だ。
二つのうちハズレの一つを開けた時点で、その扉に当りが入っている確率は 0 になる から
・・・以下省略
参考9 誤りを正そうとすると感情的になって抵抗する数学の学生がいること
Devlin, Keith (July ‐ August 2003). に、 「学生が間違えたとき、誤りを正そうとすると、頭は悪くないのに、感情的になって抵抗する者がいる。このようなことは、代数や微積分(algebra or calculus)で間違えた学生には見られない」 というようなことが書いてあった。
Rosenhouse, Jason.(2009). にも同様なことが書いてある。 日本の大学や高校の授業でも同じようなことが起きているに違いない。
Rosenhouse, Jason.(2009). にも同様なことが書いてある。 日本の大学や高校の授業でも同じようなことが起きているに違いない。
参考10 ワーディングを議論するときに、結果の確率が 1/2 になるような条件が好まれること
モンティ・ホール問題や3囚人問題の問題文の曖昧さを議論することを 「ワーディングの議論」 とよぶ。
純粋な気持ちでワーディングを論じるのであれば、 「モンティ・ホール問題や3囚人問題の問題文は "Well Defined"でないから、答えは無い」 となるはずであるが、実際には標準仮定が成立しない特定の条件を取り上げて論じることが多く、中でも switch して賞品を得る確率が 1/2 になる条件を論じる人が多い。
このことは、ワーディングの議論が 「おまじない」 の一種であることを予想させる。
ワーディングを議論すると、確率 1/2 をはじき出した無意識の確率判断能力への信頼感を取り戻す効果があるのかも知れない。
純粋な気持ちでワーディングを論じるのであれば、 「モンティ・ホール問題や3囚人問題の問題文は "Well Defined"でないから、答えは無い」 となるはずであるが、実際には標準仮定が成立しない特定の条件を取り上げて論じることが多く、中でも switch して賞品を得る確率が 1/2 になる条件を論じる人が多い。
このことは、ワーディングの議論が 「おまじない」 の一種であることを予想させる。
ワーディングを議論すると、確率 1/2 をはじき出した無意識の確率判断能力への信頼感を取り戻す効果があるのかも知れない。
参考10-2 ワーディングの議論と非条件付確率の問題設定の否定がセットになっていることが多いこと
参考11 標本空間でなく扉空間の上で考えてしまい答えが合わなくて悩むこと
標本空間の上で確率を考えずに、扉空間の上で確率を考えたために、 switch してもしなくても変わりがないという結論に至って悩んでいる人を Yahoo! 知恵袋などで見かけることがある。
モンティ・ホール問題慣れしている私ですら、それらを読むとしばらくの間悩まずには居られない。
以下はその例である。
モンティ・ホール問題慣れしている私ですら、それらを読むとしばらくの間悩まずには居られない。
以下はその例である。
同じ賞品配置の2つのゲームで別個の扉が選択され同じ扉が開けられたという想定での悩み
Yahoo! 知恵袋に出された質問に次のようなものがあった。
同じ賞品配置の2つのゲームが並行して行われたとする。
片方のゲームの挑戦者は扉1を選び、もう一方のゲームの挑戦者は扉3を選んだ。
どちらのゲームでもホストは扉2を開けた。
賞品の配置が両方のゲームで同じで開けられた扉も同じなのだから扉1が当りである確率は両者で同じになる。
同様に扉3が当りである確率も両者で同じになる。
しかしモンティ・ホール問題の解答では扉1が当りである確率は前者では 1 / 3 、後者では 2 / 3 となるので矛盾する。
同じ賞品配置の2つのゲームが並行して行われたとする。
片方のゲームの挑戦者は扉1を選び、もう一方のゲームの挑戦者は扉3を選んだ。
どちらのゲームでもホストは扉2を開けた。
賞品の配置が両方のゲームで同じで開けられた扉も同じなのだから扉1が当りである確率は両者で同じになる。
同様に扉3が当りである確率も両者で同じになる。
しかしモンティ・ホール問題の解答では扉1が当りである確率は前者では 1 / 3 、後者では 2 / 3 となるので矛盾する。
選ばなかった2つの扉の組と、選んだ扉と開けられた扉の組を比較したときの悩み
Yahoo! 知恵袋に出された質問に次のようなものがあった。
挑戦者が選ばなかった2つの扉の組合せと、挑戦者が選んだ扉とホストが開けた扉の組あわせのどちらも、当りかも知れない扉とハズレが確定した扉で構成されているので、有利さに差はない。
一方、switch することは前者を選ぶことであり、 switch しないことは後者を選ぶことである。
したがって、 switch してもしなくても有利さに差が無いはずであり、switch する方が有利だという通常の答えと食い違ってしまう。
挑戦者が選ばなかった2つの扉の組合せと、挑戦者が選んだ扉とホストが開けた扉の組あわせのどちらも、当りかも知れない扉とハズレが確定した扉で構成されているので、有利さに差はない。
一方、switch することは前者を選ぶことであり、 switch しないことは後者を選ぶことである。
したがって、 switch してもしなくても有利さに差が無いはずであり、switch する方が有利だという通常の答えと食い違ってしまう。
参考12 問題の出し方によって正答率が上がること
ホストの視点で考えさせると正答率が上がる
Krauss, Stefan and Wang, X. T. (2003). . の中の実験で、自動車(賞品)の配置パターンを考えさせ、かつ、ホストの視点で switch が有利か否かを考えさせると正答率が上がっている。
扉の枚数を百枚程度まで増やすと正答率が上がる
Page, S.E. (1998). の研究について、次のように三好一英・服部環 (2009).が紹介している。
ドアの枚数が3枚、10枚、100枚と増えるにつれて選択を変更する割合が増加する結果を報告しているらしい。ただし、サンプルサイズの点で検定力不足だそうだ。
対戦型にすると正答率が上がる (対戦型形式と標準型形式 参照)
Tubau, E. & Alonson, D. (2003). や、De Neys, W. & Vershueren, N. (2006). の実験結果から、対戦型にすると switch を選択する率が格段に上がることがわかる。
2010年1月3日の平成教育委員会にお年玉を題材とするモンティ・ホール問題が出されて全員正解だったらしいが、そのときのゲーム形式がまさに対戦型だった。
補足:
2010年1月3日の平成教育委員会にお年玉を題材とするモンティ・ホール問題が出されて全員正解だったらしいが、そのときのゲーム形式がまさに対戦型だった。
補足:
Tubau, E. & Alonson, D. (2003). の対戦型のモンティ・ホール問題はトランプなど裏を見ただけでは区別できないトランプを使っているので、厳密にはモンティ・ホール問題ではなく、「扉を区別できないモンティ・ホール問題もどき」と呼ぶべきである。
ただし数学的なとらえ方を不特定事象による条件付確率あるいは事後確率の問題設定 や、非条件付確率の問題設定に限定するのであれば、モンティ・ホール問題に数えてよいかも知れない。
De Neys, W. & Vershueren, N. (2006). の対戦型のモンティ・ホール問題は 3つのカップをテーブルに並べていると思われるので、 並んだ順でカップを区別できるかも知れない。
ただし数学的なとらえ方を不特定事象による条件付確率あるいは事後確率の問題設定 や、非条件付確率の問題設定に限定するのであれば、モンティ・ホール問題に数えてよいかも知れない。
De Neys, W. & Vershueren, N. (2006). の対戦型のモンティ・ホール問題は 3つのカップをテーブルに並べていると思われるので、 並んだ順でカップを区別できるかも知れない。
ボクサー型にすると正答率が上がる (ボクサー型ゲーム形式 参照)
Burns, B.D. & Wieths, M. (2004). によると、標準型に比べてボクサー型の方が正答率が高いらしい。
参考13 仮説事象に対応する現象と証拠事象に対応する現象の類似性が薄いと正答率が高いこと
夕食問題の正当率は3囚人問題よりも高いらしい
夕食問題では、食材の選択という仮説事象に対応する現象、すなわち食材そのものと、調理法の選択という証拠事象に対応する現象、すなわち焼くか焼かぬかが直接に対応していないことが、夕食問題の高い正答率の原因だという仮説が市川 伸一, 下條 信輔. (2010).に書かれている。
参考14 私の体験では、気味の悪さはなくならない
私がモンティ・ホール問題や 3囚人問題を知った 2010年から 3年以上がたった今 ( 2014年2月 ) も、 扉が2つ残った情景を思い浮かべると、片方が当る確率が他方の 2倍であることが腑に落ちなくなることがある。
不思議さの原因を心理学の文献で調べたり、 自分で考えたりしてきたが、 気味の悪さはなくならない。
不思議さの原因を心理学の文献で調べたり、 自分で考えたりしてきたが、 気味の悪さはなくならない。
参考15 証拠事象の現象に関する既述を読むと無意識に標本空間を切り替えてしまうこと
ホストがハズレの扉3を開いたという表現を読んだとたんに、扉3が当りの確率がゼロになったと考える人が多い。
この私もモンティ・ホール問題について考え始めた初期はそうだった。
しかし数学の確率論では、扉3が当りの確率がゼロだと言う前に、ホストが扉3を開いたという証拠事象で標本空間を絞り込むこと、言い換えると仮説事象それぞれの確率を事後確率で置き換えることを宣言しなければならない。
このことから、日常の確率概念では新たな現象 (事象ではない) が起きるたびに無意識に標本空間の切り替えがなされることがわかる。
この私もモンティ・ホール問題について考え始めた初期はそうだった。
しかし数学の確率論では、扉3が当りの確率がゼロだと言う前に、ホストが扉3を開いたという証拠事象で標本空間を絞り込むこと、言い換えると仮説事象それぞれの確率を事後確率で置き換えることを宣言しなければならない。
このことから、日常の確率概念では新たな現象 (事象ではない) が起きるたびに無意識に標本空間の切り替えがなされることがわかる。
参考16 二封筒問題で錯覚した人が似たような発言をすることがあること
二封筒問題で錯覚した人が次のような発言をすることがある。
封筒を開ける前は互角だった封筒が、封筒を開けて金額が分ると開けていない方の封筒が有利になるのはおかしい。
この発言は、モンティ・ホール問題で錯覚した人がよく行う次の発言に良く似ている。
ホストが扉を開ける前には互角だった扉が、扉の数が減るだけで片方が有利になるのはおかしい。
封筒を開ける前は互角だった封筒が、封筒を開けて金額が分ると開けていない方の封筒が有利になるのはおかしい。
この発言は、モンティ・ホール問題で錯覚した人がよく行う次の発言に良く似ている。
ホストが扉を開ける前には互角だった扉が、扉の数が減るだけで片方が有利になるのはおかしい。
参考17 二封筒問題の確率錯覚現象では事前と事後で確率を担う客体の種類が異なること
同じ 「尤度の無視」という 確率錯覚現象でもモンティ・ホール問題と二封筒問題では次のような違いがある。
- モンティ・ホール問題の確率錯覚現象では扉に着目した確率が事後の扉に引き継がれる。
- 二封筒問題の確率錯覚現象では封筒に着目した確率が事後の「お金」に引き継がれる。
参考18 マンモグラフィーや二封筒問題の確率錯覚現象ではこれほど強い不思議さを感じないこと
マンモグラフィー検査で陽性になったときにガンである確率の錯覚現象について数学的に理解した後でも、モンティ・ホール問題や三囚人問題で感じるような不思議さをほとんど感じない。
二つの封筒問題で選んだ封筒の金額が決まった後の残りの封筒の金額の確率の錯覚現象について数学的に理解した後でも不思議さをほとんど感じない。
わたしの体験や、これらについて語っているインターネット上のページの内容からそう判断できる。
二つの封筒問題で選んだ封筒の金額が決まった後の残りの封筒の金額の確率の錯覚現象について数学的に理解した後でも不思議さをほとんど感じない。
わたしの体験や、これらについて語っているインターネット上のページの内容からそう判断できる。
参考19 二封筒問題に見られる 「期待値の錯覚」 現象との類似点
二つの封筒問題では、割合は不明だが、少なからぬ頻度で、封筒を開けても期待値は変わらないと言明する人を見かける。 (二つの封筒問題の錯覚に気づかない人のために 参照)
このような 「期待値の錯覚」 現象は、期待値があたかもエネルギーか何かのように封筒の中に納まっているというメンタルモデル、すなわち 「客観期待値幻想」 が背後にあることを予感させる。 モンティ・ホール問題で残った扉の確率比が変わらないという錯覚の背後に、確率があたかもエネルギーか何かのように扉の背後に潜んでいるというメンタルモデル、すなわち 「客観確率幻想」 を予感させることに類似している。
このような 「期待値の錯覚」 現象は、期待値があたかもエネルギーか何かのように封筒の中に納まっているというメンタルモデル、すなわち 「客観期待値幻想」 が背後にあることを予感させる。 モンティ・ホール問題で残った扉の確率比が変わらないという錯覚の背後に、確率があたかもエネルギーか何かのように扉の背後に潜んでいるというメンタルモデル、すなわち 「客観確率幻想」 を予感させることに類似している。
確率の錯覚のメカニズムに関する認知心理学者による仮説
ヒューリスティク説
モンティ・ホール問題や3囚人問題のような確率の問題を、多くの人が残った扉や囚人の数だけで解こうとするのは、成長の過程で身に着けたヒューリスティク(自動化された無意識の経験則)が自動的に働くからだとする説がある。
ヒューリスティクの内容や、形成過程について、次の研究がある。
ヒューリスティクの内容や、形成過程について、次の研究がある。
◇ Shimojo, S., & Ichikawa, S. (1989).やShimojo, S., & Ichikawa, S. (1989).による「等比率ヒューリスティク」説
囚人毎に恩赦確率が異なる問題文を用いた実験によって、証拠事象の前後で囚人間の恩赦確率の比が変わらないと考えるヒューリスティクを用いる人が多いことを発見している。
Shimojo, S., & Ichikawa, S. (1989). はこのヒューリスティクを「等比率の定理」と名づけている。
Shimojo, S., & Ichikawa, S. (1989). はこのヒューリスティクを「等比率の定理」と名づけている。
2014/02/01 に 「問題構造把握失敗説」 の項からここに移動しました。
Shimojo, S., & Ichikawa, S. (1989). を受けた形で、確率の錯覚現象を次のような 2種類に分類している。
Shimojo, S., & Ichikawa, S. (1989). を受けた形で、確率の錯覚現象を次のような 2種類に分類している。
- Primary intuitive belief
「一次的直感」とでも訳すべきか?
直接的に確率を導く直感であり、「uniformity belief」 や 「"no-news, no-change" belief」 が含まれる。
それぞれ、 Shimojo, S., & Ichikawa, S. (1989). の 「"Number of cases" theorem」 (「場合の数の定理」) 、 「"Irrelevant, therefore invariant" theorem」 (「不変の定理」) に対応する。
- Secondary intuitive belief
「二次的直感」とでも訳すべきか?
計算プロセスをともなう直感であり、 「constant-ratio belief」 が含まれる。
Shimojo, S., & Ichikawa, S. (1989). の 「"Constant ratio" theorem」 (「当比率の定理」) に対応する。
◇ De Neys, W. & Vershueren, N. (2006). による「場合の数ヒューリスティク」説
年齢別の実験によって、証拠事象の後の選択肢の数で計算する number-of-cases heuristic を用いる割合が小学生では少ないことを発見している。また高学年になるにつれ、選択を変えない"stick with your pick" heuristic を使う学生の割合が減るlことも発見している。
「等比率ヒューリスティク」説ならば、当り扉や恩赦対象の囚人が決まる確率が不均一な場合に生じる確率の錯覚現象を説明できるが、「場合の数ヒューリスティク」説では説明できない。 このことから「等比率ヒューリスティク」説の方がより基本的であることがわかる。
自然頻度仮説
確率数値でなく自然頻度で考えるような問題文にすれば正答率が上がるという仮説に基づいて行われた実験がある。
◇ 小林厚子 (1998).
モンティ・ホール問題や3囚人問題を 特定事象による条件付確率あるいは事後確率の問題設定 で解くには複雑な手順が必要なので、それらの教育を受けていなければ上記のヒューリスティクによる錯覚がなかったとしても、モンティ・ホール問題や3囚人問題を解くことは困難だとしている。
そして、 3囚人問題を解くための標本空間の階層分割手順にそって、架空のデータ件数を計算させてから確率を答えさせると正答率が上がるという実験結果から、確率の錯覚の原因はベイズの定理の知識不足であって、なんらかのヒューリスティクによるものではないと結論付けている。
そして、 3囚人問題を解くための標本空間の階層分割手順にそって、架空のデータ件数を計算させてから確率を答えさせると正答率が上がるという実験結果から、確率の錯覚の原因はベイズの定理の知識不足であって、なんらかのヒューリスティクによるものではないと結論付けている。
モンティ・ホール問題について同様な実験を行って、確率型の設問よりも、度数型の設問の方が、モンティ・ホール問題の背後にあるベイズ確率の原理の理解を助ける力があると、結論付けている。
これらの実験により 「自然頻度で考えれば錯覚が減る」 ことが確かめられたのであるが、確率の錯覚のメカニズムの解明には至っていない。
問題構造把握失敗説
確率の問題構造を把握することに失敗したために確率の判断を誤るのだという説がある。
◇ Franco-Watkins, A. M. Derks, P. L., & Daugherty, M. R. P. (2003).
これを引用している論文によると、Franco-Watkins らは、ホストが扉を開けるとともに、問題の解釈をやり直してしまうと述べているらしい。
これを引用している論文によると、Johnson-Laird, らは、メンタルモデルが間違っているために確率の判断を誤るのだという説を提唱しているらしい。
モンティ・ホール問題の中のゲームを対戦型の形式 (対戦型形式と標準型形式 参照) にすると、正答率が上がるのは、対戦型の方が標準型に比べて正しいメンタルモデルが形成されやすいからだろうと述べている。
因果関係の把握の難しさに原因を求める説
三好一英・服部環 (2009).によると、 モンティ・ホール問題のように単1の結果に相互に独立な 2つの原因が関係しているコライダー構造があるために、それらの原因の間の条件付き依存関係 ( conditional dependence ) を把握するのが困難だと Glymour は述べているらしい。
モンティ・ホール問題のコライダー構造は次のようになっている。
(賞品の配置) → (ホストが開ける扉) ← (挑戦者が選んだ扉)
賞品の配置の事象と挑戦者が選んだ扉の事象はもともと独立であるが、ホストがどの扉を開けたかを条件として考慮すると独立でなくなる。
モンティ・ホール問題のコライダー構造は次のようになっている。
賞品の配置の事象と挑戦者が選んだ扉の事象はもともと独立であるが、ホストがどの扉を開けたかを条件として考慮すると独立でなくなる。
◇ 服部雅史, 西田豊, 他. (2009年ごろ). で発表された服部雅史先生の実験結果
「モンティ・ホール問題が難しい理由は、司会者がCのドアを開けたのは何故かという因果的な推論を大部分の解答者が行わないためではないか」
という説を確かめるために、
「司会者がCのドアを開けたのは、Bのドアのうしろに新車があるからではないか」という因果推定がなされやすいように変更した問題文
で実験した結果、予測どおり正答率が上がったらしい。
という説を確かめるために、
「司会者がCのドアを開けたのは、Bのドアのうしろに新車があるからではないか」という因果推定がなされやすいように変更した問題文
で実験した結果、予測どおり正答率が上がったらしい。
この論文の結論部分で、3囚人問題で正しい問題表象を構成することは困難であり、特に難しいのは尤度の理解だろうと書かれている。
標本空間を分割した後は分割数を増やせない説
人間が条件付き確率を計算するとき、 "Partition → Edit → Count"という手順を無意識にとるという説を提唱している。
Partition は 場合分けを行うことであり、Edit は起きなかった場合を刈り込むことであり、Count は条件付き確率を計算することであり、 条件付き確率の問題を解くときに無意識にこのような手順で計算してしまうため、 ひとたび不適切な標本空間を思い浮かべたが最後、それ以上に詳細な分析ができなくなるという説である。
モンティ・ホール問題に当てはめれば、 ( 扉1 が当たり、 扉2 が当たり、 扉3 が当たり ) の場合分けを思い浮かべたが最後、 ホストが開ける扉も考慮した場合分けができなくなるのである。
モンティ・ホール問題の確率錯覚現象によく似た錯覚現象に二封筒問題の錯覚現象があり、二つの封筒を開ける前の二つの封筒の金額の大小関係の確率を、封筒を開けた後の中身の金額の大小関係の確率として考えてしまう現象であるが、モンティ・ホール問題とは次のような違いがある。
Partition は 場合分けを行うことであり、Edit は起きなかった場合を刈り込むことであり、Count は条件付き確率を計算することであり、 条件付き確率の問題を解くときに無意識にこのような手順で計算してしまうため、 ひとたび不適切な標本空間を思い浮かべたが最後、それ以上に詳細な分析ができなくなるという説である。
モンティ・ホール問題に当てはめれば、 ( 扉1 が当たり、 扉2 が当たり、 扉3 が当たり ) の場合分けを思い浮かべたが最後、 ホストが開ける扉も考慮した場合分けができなくなるのである。
モンティ・ホール問題の確率錯覚現象によく似た錯覚現象に二封筒問題の錯覚現象があり、二つの封筒を開ける前の二つの封筒の金額の大小関係の確率を、封筒を開けた後の中身の金額の大小関係の確率として考えてしまう現象であるが、モンティ・ホール問題とは次のような違いがある。
- モンティ・ホール問題の確率錯覚現象では扉に着目した確率が事後の扉に引き継がれる。
- 二封筒問題の確率錯覚現象では封筒に着目した確率が事後の「お金」に引き継がれる。
問題構造の把握失敗に関するこれらののメカニズムは、前述のヒューリスティク説のメカニズムの前段で機能しているのではないかと、私は考えている。
夕食問題とモンティ・ホール問題や3囚人問題との認知心理学的な比較
市川 伸一, 下條 信輔. (2010).は、モンティ・ホール問題や3囚人問題と数学的に同型な問題として、橋田浩一氏が提案した「夕食問題」を次のように紹介している。
サンマの事前確率が 1/2 と高いのはサンマに内臓があるため脚が速いことに対応しているのだろう。
夕食問題を解くことは、3囚人問題を解くことより易しいらしい。しかし、看守の選択確率を意識させるような問題文にしても、3囚人問題を解く時にその知識をうまく活用できないことがわかっている。したがって、夕食問題でおかずがイカの場合に焼くか刺身にするかの確率 1/2 が問題文に明記されていることが、夕食問題が3囚人問題に比べて易しい理由ではないらしい。(市川 伸一, 下條 信輔. (2010).)
夕食問題が3囚人問題に比べて易しい理由について、市川 伸一, 下條 信輔. (2010)..は次のような仮説を述べている。
答えは1/5となる。夕食のオカズがイカ、マグロ、サンマのうちどれか1品である、それぞれの確率が 1/4、 1/4、 1/2 であるとする。 調理法としては、「イカは焼くかナマかの確率が 1/2 ずつ」「マグロは必ずナマ」「サンマは必ず焼く」ということが分っている。 いま、帰宅時に家から煙があがっているのが見えたとき、今日のオカズがイカである確率はどれだけか、 というのが夕食問題である。 --- 市川 伸一, 下條 信輔. (2010).から
サンマの事前確率が 1/2 と高いのはサンマに内臓があるため脚が速いことに対応しているのだろう。
夕食問題を解くことは、3囚人問題を解くことより易しいらしい。しかし、看守の選択確率を意識させるような問題文にしても、3囚人問題を解く時にその知識をうまく活用できないことがわかっている。したがって、夕食問題でおかずがイカの場合に焼くか刺身にするかの確率 1/2 が問題文に明記されていることが、夕食問題が3囚人問題に比べて易しい理由ではないらしい。(市川 伸一, 下條 信輔. (2010).)
夕食問題が3囚人問題に比べて易しい理由について、市川 伸一, 下條 信輔. (2010)..は次のような仮説を述べている。
3囚人問題ではデータ事象(Bが処刑されると看守が言ったこと)が原事象(Bが処刑されること)に直接関係しているので、「等比率の定理」などの主観的定理(ヒューリスティク)を適用した処理に誘導されやすい。夕食問題ではデータ事象(煙を見たということ)が原事象(おかずはマグロでないということ)に直接言及していないので、煙が出るのはどのようなオカズの場合かを考えた上で、その中でイカである場合の割合を求めるというベイズ的な解法へと誘導しやすい。
この仮説を平易に言い換えると次のようになるだろう。
3囚人問題では看守の言葉から質問した囚人と残りの囚人が恩赦の候補として残っていることが直接わかるため、無意識のヒューリスティクが自動起動されて、
- ①囚人だれそれが処刑だと看守が告げた→質問した囚人が恩赦か残りの囚人が恩赦かのどちらかである、
- と知らぬ間に判断が下されてしまい、
- ②囚人だれそれが処刑だと看守が告げた→質問した囚人が恩赦でたまたまその囚人の名が上げられたか残りの囚人が恩赦かのどちらかである、
- と考えることができなくなる。
- ①煙が出ている→焼いている→イカかサンマのどちらかである、
- と考えることも、
- ②煙が出ている→焼いている→イカで焼くことを選択したかサンマを選択したかどちらかである、
- と考えることも可能になる。
「私の仮説」の項で述べた「客観確率幻想」や「課題空間取り違え」、 「仮説事象と証拠事象の類似による標本空間重ね合わせ」、といった錯覚現象も関係していそうである。
モンティ・ホール問題や3囚人問題では、「ホストが扉を開ける」とか、「看守が囚人の名を上げた」とかいう表現を読んだ時点でも、扉空間 { 扉1, 扉2, 扉3 } や囚人空間 { 囚人A, 囚人B, 囚人C } を思い浮かべてしまうので、これらの錯覚に陥りやすい。
しかし、夕食問題では「煙が見えた」という表現を読むと、食材空間 { イカ, マグロ, サンマ } を思い浮かべる前に調理法空間 { ナマ, 焼く, } の方が頭に浮かぶので、これらの錯覚に陥りにくいのだろう。
私は次のようなことも、夕食問題が3囚人問題より易しい理由になっているのではないかと考えている。
3囚人問題では恩赦の決定をした権力者と、処刑される囚人の誰の名を告げるか選択する看守が別人であるため、看守の思考プロセスを想像する前に、質問した囚人が恩赦かどうかに遡らないと標本空間の時系列的階層分割にならない。
他方、夕食問題では食材を選択するのも、調理法を選択するのも同一人(仮に妻とする)であるので、調理法を選択する妻の思考プロセスを想像するだけで標本空間の時系列的階層分割になる。
夕食問題では尤度、すなわち、食材ごとの調理法選択確率が明記されていることも、夕食問題が3囚人問題より易しい理由かも知れない。
夕食問題は調理をする者と帰宅して煙を見るものの対決のような構造でもあるので、Tubau, E. & Alonson, D. (2003). に出てくる対戦型モンティ・ホール問題 (対戦型形式と標準型形式) に似ているかというと似ていない。対戦型のモンティ・ホール問題では対戦者 2人の他に、最初にカードをシャッフルする者がいるからである。
2014/03/21 に下記の一部を訂正しました。
モンティ・ホール問題や 3囚人問題では 不特定事象による条件付確率あるいは事後確率の問題設定 や 非条件付確率の問題設定 をとることが可能であるが、夕食問題では不可能ではないまでも、 非常に困難である。 「煙が出ている状況」 を 「煙が出ていたり出ていなかったりする状況」 と読み替えることは、「イカとサンマ」 の議論から 「イカとイカ以外」 の議論に切り替えることに他ならず、煙を見て排除したマグロの可能性を復活させてしまうからである。 .モンティ・ホール問題で挑戦者が選ばなかった扉2 と扉3 を区別しないことは容易であるが、夕食問題でサンマとマグロを区別しないことは簡単ではない。
しかし、このことは夕食問題で正答しやすいことの説明にはならない。 モンティ・ホール問題や 3囚人問題でも、人から教わらずに自力で 不特定事象による条件付確率あるいは事後確率の問題設定 や 非条件付確率の問題設定 に気づくことは困難だからである。
2014/03/16 に下記を書き加えました。
モンティ・ホール問題や 3囚人問題では 中間事象 に関する現象 (挑戦者が扉を選ぶことや看守に質問する囚人が現れること) が証拠事象 (ホストが開ける扉や看守が明かす囚人の名) の選択肢を二つに狭めるが、夕食問題では最初から { 焼く, 生 } の二つに限定されていることにも、2014/03/15 に気付いた。
このことは夕食問題で正当しやすいことの説明になるかも知れない。 正答率が高い対戦型のモンティ・ホール問題 (対戦型形式と標準型形式) では、ホストが表に返せるカードを彼の手に持たせてホストの選択肢の範囲を意識しやすくしている。 夕食問題の調理法が最初から二つに限定されていることが同じような効果を持っているかも知れないからである。
モンティ・ホール問題や3囚人問題では、「ホストが扉を開ける」とか、「看守が囚人の名を上げた」とかいう表現を読んだ時点でも、扉空間 { 扉1, 扉2, 扉3 } や囚人空間 { 囚人A, 囚人B, 囚人C } を思い浮かべてしまうので、これらの錯覚に陥りやすい。
しかし、夕食問題では「煙が見えた」という表現を読むと、食材空間 { イカ, マグロ, サンマ } を思い浮かべる前に調理法空間 { ナマ, 焼く, } の方が頭に浮かぶので、これらの錯覚に陥りにくいのだろう。
私は次のようなことも、夕食問題が3囚人問題より易しい理由になっているのではないかと考えている。
3囚人問題では恩赦の決定をした権力者と、処刑される囚人の誰の名を告げるか選択する看守が別人であるため、看守の思考プロセスを想像する前に、質問した囚人が恩赦かどうかに遡らないと標本空間の時系列的階層分割にならない。
他方、夕食問題では食材を選択するのも、調理法を選択するのも同一人(仮に妻とする)であるので、調理法を選択する妻の思考プロセスを想像するだけで標本空間の時系列的階層分割になる。
夕食問題では尤度、すなわち、食材ごとの調理法選択確率が明記されていることも、夕食問題が3囚人問題より易しい理由かも知れない。
夕食問題は調理をする者と帰宅して煙を見るものの対決のような構造でもあるので、Tubau, E. & Alonson, D. (2003). に出てくる対戦型モンティ・ホール問題 (対戦型形式と標準型形式) に似ているかというと似ていない。対戦型のモンティ・ホール問題では対戦者 2人の他に、最初にカードをシャッフルする者がいるからである。
2014/03/21 に下記の一部を訂正しました。
モンティ・ホール問題や 3囚人問題では 不特定事象による条件付確率あるいは事後確率の問題設定 や 非条件付確率の問題設定 をとることが可能であるが、夕食問題では不可能ではないまでも、 非常に困難である。 「煙が出ている状況」 を 「煙が出ていたり出ていなかったりする状況」 と読み替えることは、「イカとサンマ」 の議論から 「イカとイカ以外」 の議論に切り替えることに他ならず、煙を見て排除したマグロの可能性を復活させてしまうからである。 .モンティ・ホール問題で挑戦者が選ばなかった扉2 と扉3 を区別しないことは容易であるが、夕食問題でサンマとマグロを区別しないことは簡単ではない。
しかし、このことは夕食問題で正答しやすいことの説明にはならない。 モンティ・ホール問題や 3囚人問題でも、人から教わらずに自力で 不特定事象による条件付確率あるいは事後確率の問題設定 や 非条件付確率の問題設定 に気づくことは困難だからである。
2014/03/16 に下記を書き加えました。
モンティ・ホール問題や 3囚人問題では 中間事象 に関する現象 (挑戦者が扉を選ぶことや看守に質問する囚人が現れること) が証拠事象 (ホストが開ける扉や看守が明かす囚人の名) の選択肢を二つに狭めるが、夕食問題では最初から { 焼く, 生 } の二つに限定されていることにも、2014/03/15 に気付いた。
このことは夕食問題で正当しやすいことの説明になるかも知れない。 正答率が高い対戦型のモンティ・ホール問題 (対戦型形式と標準型形式) では、ホストが表に返せるカードを彼の手に持たせてホストの選択肢の範囲を意識しやすくしている。 夕食問題の調理法が最初から二つに限定されていることが同じような効果を持っているかも知れないからである。
マンモグラフィー検査とモンティ・ホール問題や3囚人問題との認知心理学的な比較
マンモグラフィーなどの癌検査では、「癌であれば何パーセントの率で見つけることができます」といった説明を受けることがあっても、「陽性になった場合に実際に癌である確率は何パーセントです」といった説明を受けることはまれである。(少なくとも 2010年ごろの日本ではそうだろう)
そのため、検査で陽性になった人は高い確率で癌になっていると心配するが、それは錯覚である。
マンモグラフィー検査の錯覚とモンティ・ホール問題の錯覚との間には次のような違いがある。
同じ事後確率の錯覚でありながら、このような違いがあることにまず驚かされるが、どちらも最後に言われた言葉にだけ着目して事後の標本空間を構成している点が共通している。
人間が確率を判断するときには、最後に聞いた言葉につられて標本空間を構成してしまう習性があるのかも知れない。
(「確率の錯覚のメカニズムに関する私の仮説」の項でも、この習性を取り上げています)
そのため、検査で陽性になった人は高い確率で癌になっていると心配するが、それは錯覚である。
マンモグラフィー検査の錯覚とモンティ・ホール問題の錯覚との間には次のような違いがある。
| 事例 | 錯覚現象 | 尤度の明示の有無 | 錯覚の内容 | 錯覚の名称 |
|---|---|---|---|---|
| マンモグラフィー検査 | 癌に掛かっているときに検査結果が陽性になる確率を陽性になったときに癌に掛かっている確率と錯覚する。 |
あり 癌に掛かっている場合と掛かっていない場合のそれぞれについて、陽性になる確率と陰性になる確率が示される。 |
癌に掛かっているという条件での陽性や陰性になる確率を事後確率と錯覚する。 |
事前確率の無視(neglect of prior probability) 基準率錯誤(base rate fallacy) (市川 伸一, 下條 信輔. (2010).による) |
| モンティ・ホール問題 | 三つの扉が当たりである確率が等しかったから、二つだけ残ったときにも当りである確率は等しいと錯覚する。 |
ない 当り扉と挑戦者が選んだ扉の組合せごとの、各扉をホストが開ける確率は明示されていない |
残った扉の確率に差異が生じるようなことは起きていないと錯覚する。 | 私は「尤度の無視」と呼ぶことにしている。 |
同じ事後確率の錯覚でありながら、このような違いがあることにまず驚かされるが、どちらも最後に言われた言葉にだけ着目して事後の標本空間を構成している点が共通している。
| 事例 | 最後に言われた言葉 | 錯覚した標本空間 |
|---|---|---|
| マンモグラフィー検査 |
(検査結果が陽性と告げた後で) 癌に掛かっているときに検査結果が |
|
|
|
ホストが扉3 を開けたので、扉1と扉2が残った |
|
人間が確率を判断するときには、最後に聞いた言葉につられて標本空間を構成してしまう習性があるのかも知れない。
(「確率の錯覚のメカニズムに関する私の仮説」の項でも、この習性を取り上げています)
確率の錯覚のメカニズムに関する私の仮説
私の見るところ、モンティ・ホール問題や3囚人問題の確率を錯覚する人の思考プロセスは次のようである。(心理学者の論文でも大体、同様である)
- ①扉に対する賞品の配置や、囚人に対する恩赦の配置だけで場合分けを行う。
- ②ホストが扉を開けたり、看守が処刑囚人の名を上げたりした後でも、ホストや看守の行動を組み込んだ精密な標本空間を組み立てることをしない。
- ③最初に思いついた単純な標本空間から起きなかった事象を除いて事後の標本空間を切り出す。
「最新情報反応」説
「直観が誤りをおかしやすい点」 という Webページで、 北岡 元 (2008). と、 印南 一路 (2002). を元に、直感 (ヒューリスティク)による確率判断が誤りやすい点が分類整理されていた。
その Web ページで紹介されているヒューリスティクの誤りのうち、 モンティ・ホール問題や3囚人問題に関係しそうなものを抜き出すと次のようになる。
その Web ページで紹介されているヒューリスティクの誤りのうち、 モンティ・ホール問題や3囚人問題に関係しそうなものを抜き出すと次のようになる。
- 条件付き確率を、確率だと認識する
- 利用可能な情報 (思い出しやすい情報) を過度に重視する
例 短期的変化にむやみに反応する。 最初あるいは最後の選択肢を重視する。 - 均一なバラツキを過度に期待する
- 有望な理由 1
上記の心理学者による説や、以下に述べる私の説の根本原理として働いていそうである。 - 有望な理由 2
モンティ・ホール問題や3囚人問題の確率の錯覚だけでなく、マンモグラフィの確率の錯覚にも適用できる。
「起きなかったことは忘れましょう」説
「現象」と「事象」の区別をきちんと教わっていないために、ホストが扉を開けたり看守が処刑される囚人の名をあげたりしたときに、扉に賞品が設定されたり囚人の恩赦が決定されたりする「現象」が再度発生したかのような計算を無意識に行ってしまうのだろう。
日常生活ではモンティ・ホール問題のように証拠事象と仮説事象の独立性が仮説事象によって差があるケースに遭遇することが少ないので、このようなヒューリスティクが身に付いてしまうのだろう。
日常生活ではモンティ・ホール問題のように証拠事象と仮説事象の独立性が仮説事象によって差があるケースに遭遇することが少ないので、このようなヒューリスティクが身に付いてしまうのだろう。
「客観確率幻想」 別名 「確からしさ=重さ」説
一般の人は「確からしさ」をその事物(客体)が持つ能力として捉えるという説である。
よい例がサイコロの目である。 本当の確率論では、サイコロの1の目が出るという事象に 「確からしさ」 が付与されるのであって、1の目そのものに 「確からしさ」 が付与されるのではない。しかし、一般の人は、サイコロの目の一つ一つがそれぞれ、同量の 「確からしさ」 を持つと考えてしまうようである。
モンティ・ホール問題なら各扉が、それぞれ 1/3 という当たりの 「確からしさ」 を持ち、 3囚人問題なら各囚人がそれぞれ 1/3 という恩赦になる 「確からしさ」 を持つように考えてしまうようである。
このような考え方を私は 「客観確率幻想」 と呼びたい。
「客観確率幻想」 がモンティ・ホール問題や3囚人問題の確率の錯覚に関係していることは、当りにする扉の決め方や、恩赦にする囚人の決め方が等確率で無いケースで、 扉単位の事前確率の比率を保存しつつ事後確率を判断する傾向があることからわかる。
客観確率幻想に陥っている人、 つまり私を含めた人類一般の頭の中で起きていることと、 標本空間で確率を考える人、 つまり場合分けをしっかりやらないとモンティ・ホール問題や3囚人問題を間違えることを知った人の頭の中で起きていることを比較した図解を、「モンティ・ホール問題と3囚人問題の概要」 の項の 「確率を錯覚する理由の手っ取り早い説明 」 の項で、試みているので、そちらもご一読いただきたい。
よい例がサイコロの目である。 本当の確率論では、サイコロの1の目が出るという事象に 「確からしさ」 が付与されるのであって、1の目そのものに 「確からしさ」 が付与されるのではない。しかし、一般の人は、サイコロの目の一つ一つがそれぞれ、同量の 「確からしさ」 を持つと考えてしまうようである。
モンティ・ホール問題なら各扉が、それぞれ 1/3 という当たりの 「確からしさ」 を持ち、 3囚人問題なら各囚人がそれぞれ 1/3 という恩赦になる 「確からしさ」 を持つように考えてしまうようである。
このような考え方を私は 「客観確率幻想」 と呼びたい。
「客観確率幻想」 がモンティ・ホール問題や3囚人問題の確率の錯覚に関係していることは、当りにする扉の決め方や、恩赦にする囚人の決め方が等確率で無いケースで、 扉単位の事前確率の比率を保存しつつ事後確率を判断する傾向があることからわかる。
客観確率幻想に陥っている人、 つまり私を含めた人類一般の頭の中で起きていることと、 標本空間で確率を考える人、 つまり場合分けをしっかりやらないとモンティ・ホール問題や3囚人問題を間違えることを知った人の頭の中で起きていることを比較した図解を、「モンティ・ホール問題と3囚人問題の概要」 の項の 「確率を錯覚する理由の手っ取り早い説明 」 の項で、試みているので、そちらもご一読いただきたい。
「課題空間取り違え」説
数学の確率論では、「標本空間」の中の「事象」にシグマ代数構造を満たす「測度」が付与されたとき、その「測度」をその「事象」の「確率」と称する。
しかし、私を含む普通の人はこのように「標本空間」から出発する厳密な「確率」の定義を習わないため、まったく別の空間上で確率を考えることが多そうである。
j実際、モンティ・ホール問題について語る人の多くは、扉の枚数が減ったとか、扉3が無くなったとか、扉の配置に目が行ってしまう。
そのため、見当違いな空間上で確率の問題を考えてしまって答えと間違えたり、正解を理解しても納得が行かなかったりするのだろう。
このような心の働きが、「起きなかったことは忘れましょう」説や、「確からしさ=重さ」説が予想する心の働きの元になっているのかも知れない。
なお、この説は前に上げた心理学者による 「問題構造把握失敗説」 に似たところがある。
しかし、私を含む普通の人はこのように「標本空間」から出発する厳密な「確率」の定義を習わないため、まったく別の空間上で確率を考えることが多そうである。
j実際、モンティ・ホール問題について語る人の多くは、扉の枚数が減ったとか、扉3が無くなったとか、扉の配置に目が行ってしまう。
そのため、見当違いな空間上で確率の問題を考えてしまって答えと間違えたり、正解を理解しても納得が行かなかったりするのだろう。
このような心の働きが、「起きなかったことは忘れましょう」説や、「確からしさ=重さ」説が予想する心の働きの元になっているのかも知れない。
なお、この説は前に上げた心理学者による 「問題構造把握失敗説」 に似たところがある。
「仮説事象と証拠事象の類似による標本空間重ね合わせ」説
最初に、ホストや看守の行動を組み込んでいない単純な標本空間を思い浮かべてしまうと、ホストが扉を開けたり、看守が処刑される囚人の名をあげた後でも、ホストや看守の行動を組み込んで標本空間を組みなおすことになかなか思い至らない。
このようなことがなぜ起こるのか、仮説事象と証拠事象の構造が一致し、しかもそれらの現象の客体も同一であるためにそれらを掛け合わせて標本空間を構成するのでなく、ついつい、それらを重ね合わせて単純に事後の標本空間を思い浮かべてしまうという説を、 「課題空間取り違え」説 を考えているときに思いついた。
モンティ・ホール問題や3囚人問題の仮説事象と証拠事象を図にすると次のようになる。
左側がモンティ・ホール問題、右側が3囚人問題である。
仮説事象と証拠事象の現象の客体は次のようである。
このように仮説事象と証拠事象が一致し、しかもそれらの現象の客体が同一であるため、ホストが扉3を開けたり、看守が囚人Bが処刑だと告げたりすると、仮説事象の構造の上に証拠事象の構造を重ね合わせて事後の標本空間を考えてしまうのだろう。
仮説事象と証拠事象の現象の客体が同一であることの重要性は、マンモグラフィ検査などのガン検診に関する確率の錯覚と比較するとわかる。
マンモグラフィ検査などで陽性なったときのガンに罹っている確率の場合、仮説事象と証拠事象の構造が一致しているが、仮説事象と証拠事象の現象の客体は異なっている。
単純にするため、ガンには「罹っている」と「罹っていない」の2つの状態しかないとすると、マンモグラフィ検査の仮説事象と証拠事象を図にすると次のようになる。
仮説事象の現象の客体は乳腺という実体であり、証拠事象の現象の客体はマンモグラフィィ検査というプロセスであって、心理的に異質なものであることがガン検診の確率の錯覚を数学的に説明された後の不思議さがモンティ・ホール問題や3囚人問題より弱いことと関係していそうである。
上記の説を考えるに当って、市川 伸一, 下條 信輔. (2010).の中の、「3囚人問題ではデータ事象(Bが処刑されると看守が言ったこと)が原事象(Bが処刑されること)に直接関係しているので、「等比率の定理」などの主観的定理(ヒューリスティク)を適用した処理に誘導されやすい」という説も参考にしました。
なお、この説は前に上げた心理学者による 「コライダー構造だから因果関係の把握が難しいとする説」 に似たところがある。
このようなことがなぜ起こるのか、仮説事象と証拠事象の構造が一致し、しかもそれらの現象の客体も同一であるためにそれらを掛け合わせて標本空間を構成するのでなく、ついつい、それらを重ね合わせて単純に事後の標本空間を思い浮かべてしまうという説を、 「課題空間取り違え」説 を考えているときに思いついた。
モンティ・ホール問題や3囚人問題の仮説事象と証拠事象を図にすると次のようになる。
左側がモンティ・ホール問題、右側が3囚人問題である。
| 仮説事象 | |||||||
|
| ||||||
| 証拠事象 | |||||||
|
| ||||||
仮説事象と証拠事象の現象の客体は次のようである。
|
|
|
|
|---|---|---|
|
|
扉 | 囚人 |
| 3囚人問題 | 扉 | 囚人 |
このように仮説事象と証拠事象が一致し、しかもそれらの現象の客体が同一であるため、ホストが扉3を開けたり、看守が囚人Bが処刑だと告げたりすると、仮説事象の構造の上に証拠事象の構造を重ね合わせて事後の標本空間を考えてしまうのだろう。
| 事後の標本空間 | |||||||
|
| ||||||
仮説事象と証拠事象の現象の客体が同一であることの重要性は、マンモグラフィ検査などのガン検診に関する確率の錯覚と比較するとわかる。
マンモグラフィ検査などで陽性なったときのガンに罹っている確率の場合、仮説事象と証拠事象の構造が一致しているが、仮説事象と証拠事象の現象の客体は異なっている。
単純にするため、ガンには「罹っている」と「罹っていない」の2つの状態しかないとすると、マンモグラフィ検査の仮説事象と証拠事象を図にすると次のようになる。
仮説事象
証拠事象
|
仮説事象の現象の客体は乳腺という実体であり、証拠事象の現象の客体はマンモグラフィィ検査というプロセスであって、心理的に異質なものであることがガン検診の確率の錯覚を数学的に説明された後の不思議さがモンティ・ホール問題や3囚人問題より弱いことと関係していそうである。
上記の説を考えるに当って、市川 伸一, 下條 信輔. (2010).の中の、「3囚人問題ではデータ事象(Bが処刑されると看守が言ったこと)が原事象(Bが処刑されること)に直接関係しているので、「等比率の定理」などの主観的定理(ヒューリスティク)を適用した処理に誘導されやすい」という説も参考にしました。
なお、この説は前に上げた心理学者による 「コライダー構造だから因果関係の把握が難しいとする説」 に似たところがある。
「因果関逆転」説
通常の確率の問題では、証拠事象から仮説事象に向かう因果関係があるので、証拠事象が仮説事象の確率にどのように影響するかを考えて確率を計算する。
例えば天気予報の場合、低気圧が近づいたという証拠事象を考慮して、雨が降るという仮説事象の確率を上げる。
それに対して事後確率の問題では、仮説事象から証拠事象に向かう因果関係があるので、仮説事象が証拠事象を発生させる尤度と、仮説事象の事前確率を掛けたものを、対立する仮説事象同士で比較しなければならない。
そういう計算の必要性に気づかずに、「事後確率の問題を解くときに、通常の確率と同様に、証拠事象から仮説事象に向かう因果関係を探して、それらしきものが見つかると、それにとびついて、単純な構造で確率を計算してしまうのだ」という説を 「因果関逆転説」 と呼びたい。
例えば、モンティ・ホール問題の場合、ホストが扉3 を開けたという証拠事象が、扉1が当たりである事象や、扉2 が当たりである事象に与える因果関係を探し始めてしまい、そうしているうちに扉の数が 3 から 2 に減ったという現象を発見して、それにすがって、2枚の扉で構成される空間の上で確率を考えてしまうのだろう。
マンモグラフィーの場合であれば、検査結果が陽性であったという証拠事象が、乳ガンに罹っているという事象に与える因果関係を探して、乳ガンに罹っている場合に陽性になる確率を陽性の場合に乳ガンに罹っている確率と混同してしまうのだろう。
例えば天気予報の場合、低気圧が近づいたという証拠事象を考慮して、雨が降るという仮説事象の確率を上げる。
それに対して事後確率の問題では、仮説事象から証拠事象に向かう因果関係があるので、仮説事象が証拠事象を発生させる尤度と、仮説事象の事前確率を掛けたものを、対立する仮説事象同士で比較しなければならない。
そういう計算の必要性に気づかずに、「事後確率の問題を解くときに、通常の確率と同様に、証拠事象から仮説事象に向かう因果関係を探して、それらしきものが見つかると、それにとびついて、単純な構造で確率を計算してしまうのだ」という説を 「因果関逆転説」 と呼びたい。
例えば、モンティ・ホール問題の場合、ホストが扉3 を開けたという証拠事象が、扉1が当たりである事象や、扉2 が当たりである事象に与える因果関係を探し始めてしまい、そうしているうちに扉の数が 3 から 2 に減ったという現象を発見して、それにすがって、2枚の扉で構成される空間の上で確率を考えてしまうのだろう。
マンモグラフィーの場合であれば、検査結果が陽性であったという証拠事象が、乳ガンに罹っているという事象に与える因果関係を探して、乳ガンに罹っている場合に陽性になる確率を陽性の場合に乳ガンに罹っている確率と混同してしまうのだろう。
上記の私の説の整理
上記の私の説の内、 「課題空間取り違え」説 や 「仮説事象と証拠事象の類似による標本空間重ね合わせ」説 は、 「客観確率幻想」別名「確からしさ=重さ」説 の結果であると考えられるので、「客観確率幻想」別名「確からしさ=重さ」説 に含めることとした。
理解しても納得できないのは何故かに関する認知心理学者による仮説
このような観点で行われた心理学的研究を私は知らない。
理解しても納得できないのは何故かに関する私の仮説
「客観確率幻想」 別名 「確からしさ=重さ」説
前に述べたように、一般の人は「確からしさ」をその事物(客体)が持つ能力として捉えるという説である。
繰り返しになるが、モンティ・ホール問題なら各扉が、それぞれ 1/3 という当たりの「確からしさ」を持ち、3囚人問題なら各囚人がそれぞれ 1/3 という恩赦になる「確からしさ」を持つように考えてしまうようである。
このような客観確率幻想があるため、残った二つの扉が当りである確率に違いが生じたり、残った二人の囚人の恩赦になる確率に違いが生じることが受け入れられないのだろう。
客観確率幻想が確かにあることは、次のような人間の振る舞いからも予想される。
繰り返しになるが、モンティ・ホール問題なら各扉が、それぞれ 1/3 という当たりの「確からしさ」を持ち、3囚人問題なら各囚人がそれぞれ 1/3 という恩赦になる「確からしさ」を持つように考えてしまうようである。
このような客観確率幻想があるため、残った二つの扉が当りである確率に違いが生じたり、残った二人の囚人の恩赦になる確率に違いが生じることが受け入れられないのだろう。
客観確率幻想が確かにあることは、次のような人間の振る舞いからも予想される。
- ◇モンティ・ホール問題や 3囚人問題を理解したということは、標本空間という抽象空間の上で確率を考えたということであり、必然的に客観確率幻想と相容れない。 そのような不思議さ、あるいは不気味さから逃れるために、「事後確率は主観確率の一種だ」などと、哲学 (確率解釈論) を持ち出す人がいるが、こういう人は、人間の意識の中の客体が確率を担っていると考えているのではないだろうか。
- ◇挑戦者が選ばなかった二つの扉を合わせた確率が「そのまま」残った1つの扉に継承されると考えたり、看守に質問した囚人以外の二人の囚人を合わせた確率が「そのまま」残った一人の囚人に継承されると考えたり、する人がいるが、まさに扉や囚人にエネルギーか質量のごとくに確率がやどっていると考えているのだろう。
理解して不思議さが薄まっても気味の悪さが残るのは何故かに関する私の仮説
この問題に関しては、
「不思議さが薄まっても気味の悪さが残るわけ」 を参照されたい。
これまでに述べた心理学者や私の説の比較評価(わたしによる個人的評価)
※この表はちょくちょく書き直しています。
※注 : 対戦型のゲーム形式にすると、別種のヒューリスティクが働き始めると考えられる。
| 仮説 | 統計数学者も錯覚する理由になるか | 確率が 1/2 だと勘違いする理由になるか | 正解に納得できない理由になるか | 怪しげな説明を考え出す理由になるか | マンモグラフィ検査よりモンティ・ホール問題の方が不思議さが強いことを説明できるか |
対戦型のゲーム形式にすると正答率が上がることを説明できるか (対戦型形式と標準型形式参照) |
|---|---|---|---|---|---|---|
| 心理学者による 「ヒューリスティク説」 | 〇 | 〇 | △ | × | 〇 |
△ ※注参照 |
| 心理学者による 「コライダー構造説」 | △ | 〇 | △ | × | 〇 | △ |
| 心理学者による 「仮説事象と証拠事象類似説」 | △ | 〇 | △ | × | 〇 | △ |
| 心理学者による 「尤度着目失敗説」 | △ | 〇 | △ | × | × | △ |
| 心理学者による 「標本空間を分割した後は分割数を増やせない説」 | 〇 | 〇 | △ | × | × | △ |
| 私の「最新情報反応」説 | 〇 | 〇 | × | × | × | × |
| 私の「起きなかったことは忘れましょう」説 | × | 〇 | 〇 | △ | × | × |
| 私の「客観確率幻想」別名「確からしさ=重さ」説 | 〇 | 〇 | 〇 | 〇 | 〇 |
△ ※注参照 |
| 私の「因果関係逆転」説 | 〇 | 〇 | 〇 | 〇 | 〇 | △ |
不思議さを払う「おまじない」の心理
モンティ・ホール問題や3囚人問題の答えを理解しつつも不思議さが消えない人々は、不思議さを解消するような説明を求めて考え続け、納得できる説明を発見したと思っては他の人に説明したりすることが多い。
そのような説明は、私の知る限りすべて数学的にデタラメである。数学的な説明を理解したことが不思議さの原因なのだから、不思議さを解消する力を持つ説明が数学的にデタラメなのは当然である。
これらの「おまじない」を下記のように分類できるのではないかと私は考える。
そのような説明は、私の知る限りすべて数学的にデタラメである。数学的な説明を理解したことが不思議さの原因なのだから、不思議さを解消する力を持つ説明が数学的にデタラメなのは当然である。
これらの「おまじない」を下記のように分類できるのではないかと私は考える。
分類1 : 対抗するヒューリスティクの力を借りる「おまじない」
例:モンティ・ホール 問題で扉を増やして考える「おまじない」
扉の数を大幅に増やした場合を想像すると、switchした方が有利であることを納得しやすいことがわかっている。1990年の Marilyn vos Savant による説明が、そうした例の一つであり、その説明を要約すると次のようになる。
百万枚の扉があって、あなたが扉1を選んだと仮定してください。当たりの扉を絶対開けないホストが777,777番目の扉を残して全部開けたなら、あなたは777,777番目の扉に切り替えるでしょう?
(j実際の文章はvos Savant, Marilyn (1990).参照)
扉の枚数が3枚であろうが百万枚であろうが数学的には全く違いが無いにも関わらず、扉の枚数が桁違いに多くなると switch が有利だという正解に納得する人が多くなることから、扉3枚と扉百万枚とでは認知心理学的に大きな違いがあることがわかる。
扉の枚数が3枚であろうが百万枚であろうが数学的には全く違いが無いにも関わらず、扉の枚数が桁違いに多くなると switch が有利だという正解に納得する人が多くなることから、扉3枚と扉百万枚とでは認知心理学的に大きな違いがあることがわかる。
私の仮説(1)
最初に選んだ扉1が当たりである確率が余りにも小さいので扉1が当たりである可能性は事実上ゼロに等しいと考え、その後で何が起きても扉1が当たりであることは考慮しないというヒューリスティクに基づいた判断かも知れない。もしそうだとすると宝くじを買うような人たちは扉百万枚の説明に納得しないことが多いかも知れない。
私の仮説(2)
扉が3枚だけのときは、扉2が当たりだからホストが扉3を開けたということがそれほど強くイメージされないが、扉が百万枚のときは、扉777,777が当たりだから、それをうっかり開けないように注意しつつ残りの999,998枚を開けたという情景が強くイメージされるのかも知れない。つまり、多くの中から意図的に1つが選ばれたときには、あてずっぽう以外の要因を考えるというヒューリスティクがあるのかも知れない。
分類2 : 標本空間でなく、扉空間や囚人空間で考えて正解に導くようなロジックをひねる「おまじない」
例:「確率継承説」をとなえる「おまじない」
典型的には次のような図で説明しようとする「おまじない」である。
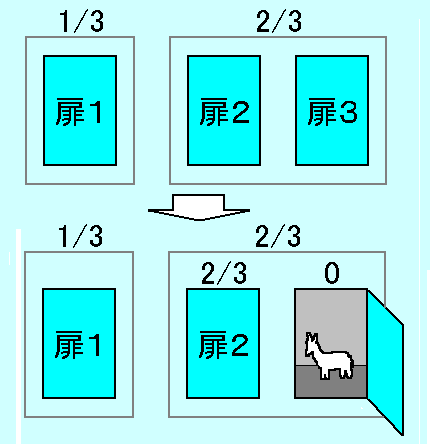
この説明が数学的に誤りであることは、 「ちまたで見かける「確率継承説」による説明 」で説明しているので ごらんください。
扉1、扉2、扉3から構成される「扉空間」の上で確率を考えつつ、標本空間の上での計算と同じ数値になることが、この「おまじない」の特徴である。
扉や囚人のような客体の空間の上で確率を考えるという日常的な考え方に誤りが無いことを確認しようとして、このような「おまじない」が唱えられるのだろう。
この説明が数学的に誤りであることは、 「ちまたで見かける「確率継承説」による説明 」で説明しているので ごらんください。
扉1、扉2、扉3から構成される「扉空間」の上で確率を考えつつ、標本空間の上での計算と同じ数値になることが、この「おまじない」の特徴である。
扉や囚人のような客体の空間の上で確率を考えるという日常的な考え方に誤りが無いことを確認しようとして、このような「おまじない」が唱えられるのだろう。
分類3 : 客観確率幻想を満たそうとする「おまじない」
例:ゲームの途中に宇宙人が来た場合を考える「おまじない」
モンティ・ホール問題のゲームの途中で空飛ぶ円盤で宇宙人がやって来て、挑戦者もホストも逃げてしまったような場合を考えて、扉2枚に賞品一つという条件だけになるので、確率が 1/2 になることを述べて安心しようとする「おまじない」である。
この説明のように宇宙人にとって確率が1/2 になるのは、モンティ・ホール問題のゲームの途中であることを宇宙人自身が知っているような状況、あるいはそのような状況であることを知っている人間あるいは宇宙人が経緯を見守っているような状況であり、数学的には「ご都合主義」といわざるを得ない。どうやら、確率が立場によって異なることを理解するために、この「おまじない」が唱えられているのではなさそうである。
この「おまじない」の真の目的は、客体自体の中に確率が潜んでいるという「客観確率幻想」の正当性を再確認することではないかと、私は考えている。
この説明のように宇宙人にとって確率が1/2 になるのは、モンティ・ホール問題のゲームの途中であることを宇宙人自身が知っているような状況、あるいはそのような状況であることを知っている人間あるいは宇宙人が経緯を見守っているような状況であり、数学的には「ご都合主義」といわざるを得ない。どうやら、確率が立場によって異なることを理解するために、この「おまじない」が唱えられているのではなさそうである。
この「おまじない」の真の目的は、客体自体の中に確率が潜んでいるという「客観確率幻想」の正当性を再確認することではないかと、私は考えている。
分類4 : 証拠事象の前後の標本空間のつながりに気付かせる「おまじない」
例:どの扉が当たりか知っているホストがヒントを与えてくれたと唱える「おまじない」
どの扉が当たりかを知っているホストの行動がヒントになって、「確率が変わる」と唱える「おまじない」である。
標準仮定の下ではゲームが始まる前から確率の値は決まっているので、この「おまじない」が数学的にデタラメであることがわかる。
この「おまじない」を唱えると、ホストが扉を開ける前後の標本空間につながりがあることが、なんとなく理解できるのだろう。
標準仮定の下ではゲームが始まる前から確率の値は決まっているので、この「おまじない」が数学的にデタラメであることがわかる。
- ①現象が起きるたびに無意識に標本空間を切り替える
- ②扉や囚人など客体の上で確率を考える
この「おまじない」を唱えると、ホストが扉を開ける前後の標本空間につながりがあることが、なんとなく理解できるのだろう。
その他の確率錯覚現象
標本空間単純化型錯覚現象
モンティ・ホール問題と3囚人問題やマンモ・グラフィ検査の確率錯覚現象には、2次元や3次元の標本空間を考えるべきところを、最後に言われた言葉だけを頼りに1次元の単純な標本空間を考えているという共通点がある。
同じ特徴を持った錯覚現象には次のようなものもある。
同じ特徴を持った錯覚現象には次のようなものもある。
|
|
|
|
|
錯覚した標本空間 |
|---|---|---|---|---|
|
Boy or Girl paradox (The Two Children Problem) |
ある人は二人の子供を持っている。少なくとも一人は男の子である。二人とも男の子である確率を問われて、1/2 と錯覚する。 | 少なくとも一人は男の子である。 | 「少なくとも一人は」と形容された男の子を「特定」の男の子と錯覚して、その子以外の子供の性別で標本空間を作ってしまう。 |
|
確率を「量」のように考えるタイプの確率錯覚現象
「率」である確率を「量」であるかのように考えて計算すると、結果を勘違いすることがある。
※ ド・メレは、パスカルが確率論を研究する切っ掛けとなった質問を出したことで有名
| 事例 | 錯覚現象 | 錯覚の内容 |
|---|---|---|
|
パスカルの三角形との関連で有名な16世紀フランス貴族シュヴァリエ・ド・メレの錯覚 (※注1) |
1 つのサイコロを4回投げて6の目が出れば自分の勝ちという賭けで勝つ確率を 1/6 × 4 = 2/3 のように計算して実際に賭けを行って儲けた。 これに味をしめて、2 つのサイコロを24回投げて「6のぞろ目」が出れば自分の勝ちという賭けで勝つ確率を 1/36 × 24 = 2/3 のように計算して実際に賭けを行って損をした。 |
24回のサイコロ振りのそれぞれに「6のぞろ目」の確率 1/36 が「量」のように配分されていると勘違いして、その合計が24回のサイコロ振りを通しての確率だと錯覚した。 |
| 集めた人間の中に同じ誕生日の二人がいる確率が 1/2 より大きくなるためには、何人集めればよいか | たった23人で充分と聞いて驚く |
ある二人の誕生日が一致する確率は 1 /365 である。 このことから、おぼろげに、 365 / 2 = 約130人 ぐらいは必要だろうと錯覚する。 |
条件付確率の確率錯覚現象
このようなものがあります。
| 事例 | 錯覚現象 | 最後に言われた言葉 | 錯覚の内容 |
|---|---|---|---|
| グレーの背広のサラリーマンは車に轢かれやすい | 背広を着ながら車に轢かれたサラリーマンの背広にグレーが多いことから、グレーの背広は危険だと錯覚する。 | 背広を着ながら車に轢かれたサラリーマンの背広にグレーが多い。 |
もともと、サラリーマンの背広はグレーが多いことを忘れて、 背広の色毎の事故率の比と 事故に合ったサラリーマンの背広の色の割合の比を混同している。 |
心理学者による研究内容
モンティ・ホール問題と3囚人問題の心理学的研究は、ヒューリスティクに関するもの以外にも多岐に渡っていて、認知、学習、発達、行動経済学などのジャンルで研究されている。
心理学的な観点では、モンティ・ホール問題と3囚人問題を区別しないことが多い。
モンティ・ホール問題の標準的な問題文では switch すべきか否かの意思決定を問い、3囚人問題の標準的な問題文では確率の値を問うている。そのためか、モンティ・ホール問題の心理学実験ではswitchするかどうかの選択課題を使っていることが多く、3囚人問題の心理学的実験では確率の値を求める課題を使うことが多い。
3囚人問題の心理学研究の歴史はモンティ・ホール問題の心理学研究よりも古い。
心理学的な観点では、モンティ・ホール問題と3囚人問題を区別しないことが多い。
モンティ・ホール問題の標準的な問題文では switch すべきか否かの意思決定を問い、3囚人問題の標準的な問題文では確率の値を問うている。そのためか、モンティ・ホール問題の心理学実験ではswitchするかどうかの選択課題を使っていることが多く、3囚人問題の心理学的実験では確率の値を求める課題を使うことが多い。
3囚人問題の心理学研究の歴史はモンティ・ホール問題の心理学研究よりも古い。
参考文献
3囚人問題に関する心理学的研究の参考文献
- ◇Wikipedia(日本語版)の「3囚人問題」の記事(2010年10月24日現在)に参考文献が記載されていて、その一部について内容あるいは書評をインターネットで読むことができた。
モンティ・ホール問題に関する心理学的研究の参考文献
- ◇三好一英・服部環 (2009).がモンティ・ホール問題に関する心理学的研究を多数紹介している。
- ◇Wikipedia(英語版) の"Monty Hall problem"の記事で参考文献としてあがっている心理学的研究の文献のいくつかについて、インターネットで読むことができた。
- ◇マリリン・ヴォス・サヴァント著 「気がつかなかった数学の罠 論理思考トレーニング法」
東方雅美訳 中央経済社刊 (2002) の巻末付録として、 ドナルド・グランバーグ著「モンティ・ホール・ジレンマ ‐変えるべきか 変えざるべきか‐」 (Granberg, Donald (1996). ) を読むことができる。
正答率に関する報告
De Neys, W. & Vershueren, N. (2006). によると、大学生の中で switch という正答を与える学生の割合が少なく、下記の論文でも 9% ~ 21% の範囲にとどまっている。
Burns, B.D. & Wieths, M. (2004). ; Friedman, D. (1998). ; ;Granberg, Donald and Brown, Thad A. (1995). ; Krauss, Stefan and Wang, X. T. (2003). ; Tubau, E. & Alonson, D. (2003).
Study1 大学生228名にアンケート調査したところ、switchを選択した者が13%のみであった。
Krauss, Stefan and Wang, X. T. (2003). によると、このときGranberg が使用した問題文は「モンティは必ず挑戦者が選ばなかったハズレのドアを開ける」という文言を加えたバージョンだったらしい。
Krauss, Stefan and Wang, X. T. (2003). によると、このときGranberg が使用した問題文は「モンティは必ず挑戦者が選ばなかったハズレのドアを開ける」という文言を加えたバージョンだったらしい。
Tubau, E. & Alonson, D. (2003). の第1実験で、コンピュータを使ったゲームを反復した場合の学習効果の実験を行っている。ゲームを開始する前に switch が有利だと解答した者は 57人中 11人であったらしい。そのうちの 7人が、ゲームを45回行った後に考えを変えている。
標準仮定の明記が正答率に与える効果に関する研究
Shimojo, S., & Ichikawa, S. (1989). によると、 看守が囚人Aに処刑される囚人の名を告げるとき、囚人Aが恩赦のとき囚人BとCのどちらを選ぶかという選択確率が等確率であると明記した問題文と、必ずBの名を告げると明記した問題文を使って実験したところ、質問した囚人が恩赦になる事後確率について、前者の問題文で確率 1 / 3 という回答が大きな割合をしめるわけでも、後者の問題文で 1 / 2 という回答が大きな割合をしめるわけではなかった。
【補足】
【補足】
論文の中の図を見ると、後者の問題文を前者の問題文の前に提示した方が、後に提示したときより、 後者の問題文に対する 1 / 2 という回答の割合が多い。
Granberg, Donald and Brown, Thad A. (1995). の研究について Krauss, Stefan and Wang, X. T. (2003). は次のように紹介している。
Granberg, Donald (1996). には上記の実験で使われた問題文が載っていて、 その問題文の冒頭で司会者がうそをつかないことを明記し、そして司会者自身に 「残りの二つのドアのうちヤギの居るドアを開けます」 と言わしめている。Consequently, most experimental psychologists insert the intended rule “Monty has to open another door and reveal a goat” into the standard version to avoid criticism about ambiguity in the wording. But this does not seem to help participants: Although Granberg and Brown (1995) stressed this rule, they observed only 13% switch decisions. ---Krauss, Stefan and Wang, X. T. (2003). から
このように標準仮定の主要部分を明確にしても、問題文を読んだミズーリ大学の学生 228 人のうち 13% しか扉を switch しなかった。
Krauss, Stefan and Wang, X. T. (2003). は、 「等確率開扉の仮定」 以外の標準仮定を明記した問題文を使って実験してみたが、確信を持って switch の方が有利だとしている回答は 5~6% にとどまっている。(確信無しに switch を選択した回答も含めると switch を選択した回答は 21~23% である)
De Neys, W. & Vershueren, N. (2006). の中の 「等確率開扉の仮定」 以外の標準仮定を明記した問題文 ( Krauss, Stefan and Wang, X. T. (2003). が実験で使ったものがベース ) を使った実験で、大学生の被験者で switch を選択した回答が 5.2% にとどまっている。
標準仮定が成立する問題文と成立しない問題文での switch する比率の比較
Granberg, Donald (1996). によると、ホストが当り扉を知っていてそれを開けないようにする問題文と、当り扉を知らないため、当り扉を開けるかも知れない問題文を使った実験結果は次のようであった。
| 知っている | 15% がswitch |
| 知らない | 10% がswitch |
Mueser, Peter R. and Granberg, Donald (May 1999). では、ホストが当り扉を開けることもあるとした問題文と比較した実験を行っている。
| 問題文の性格 |
被験者の割合 |
|---|---|
|
Monty Hall Standard |
19% |
|
Monty Hall Ambiguous |
11% |
|
Monty Hall Random |
18% |
ヒューリスティクの発達心理学的研究
DeNeys, W.(2006). は、一般人が確率の問題を解くときのヒューリスティクについて次のような結果を得ている。
モンティ・ホール問題を解くときに使うヒューリスティクには number-of-cases heuristic (場合の数ヒューリスティク)と、"stick with your pick" heuristic (「選択を変えるな」ヒューリスティク) がある。
number-of-cases heuristic を使った人は「変更してもしなくても同じ」と答え、"stick with your pick" heuristic を使った人は「変更しない」と答える。
Krauss, Stefan and Wang, X. T. (2003). が作成した曖昧さを除去したバージョンのモンティ・ホール問題を使い、大学生と高校生を使って実験したところ、次のような結果を得た。
ほとんどの大学生が number-of-cases heuristic を使った。
number-of-cases heuristic を使う生徒の割合は、年齢が増すにつれて増える。
"stick with your pick" heuristic を使う学生の割合は、年齢が増すにつれて減る。
switch と答えた生徒は12歳前後の学生たちだけであった。
switch と正解を答えた生徒は特に認知能力が高くはないので、直感で答えたに過ぎない。
高校生では number-of-cases heuristic を使った生徒ほど、認知能力が高い。
大学生ほどの年齢になると自動的に number-of-cases heuristic を使っている。
※ number-of-cases heuristic の研究として、Shimojo, S., & Ichikawa, S. (1989).を引用している。
人間と他の種とを比較した実験
Herbranson, W. T. and Schroeder, J. (2010). は、モンティ・ホール問題のゲームを使った学習心理学の実験について、被験者がハトの場合と、人間の場合との成績を比較して次のような結果を得ている。
ハトを被験者とした実験
装置
3個のキーと1つの給餌口の付いた実験装置
反復回数
一週当たり5日、同じ時刻の実験セッション
初日10回、最後100回の試行
初日10回、最後100回の試行
実験結果
初日 switch 36.33%
30日目 switch 96.33%
30日目 switch 96.33%
学生を被験者とした実験
装置
タッチセンサー付きモニターに3センチ角の四角形を3つ並べて見せ、試行を反復して学習の成績を調べる。
反復回数
1実験セッション = 4ブロック
1ブロック = 50試行
1ブロック = 50試行
実験結果
最初のブロック switch 56.67%
最後のブロック switch 65.67%
最後のブロック switch 65.67%
論文の最後"General Discussion"で、「人間の方がハトより成績が悪いことの原因は、認知の発達過程で身に付けたヒューリスティクの影響かも知れない。」と述べている。
標本空間の階層分割の手順に添いながら具体的な頻度を計算させると正答率が高いという実験
特定事象による条件付確率あるいは事後確率の問題設定に関して次のような実験がある。
小林厚子 (1998). は、3囚人問題を解くための標本空間の階層分割手順にそって、架空のデータ件数を計算させてから確率を答えさせると正答率が上がると報告している。報告された実験のあらましは次のとおり。
小林厚子 (1998). は、3囚人問題を解くための標本空間の階層分割手順にそって、架空のデータ件数を計算させてから確率を答えさせると正答率が上がると報告している。報告された実験のあらましは次のとおり。
A型の質問紙による実験
被験者は文科系の大学一年生 142人
標準的な3囚人問題の問題文に続けて、恩赦確率にばらつきのある変形3囚人問題の問題文に答えさせる。
解く為のヒントも手順も示さずに、いきなり確率を答えさせている。(選択問題形式)
標準的な3囚人問題の問題文に続けて、恩赦確率にばらつきのある変形3囚人問題の問題文に答えさせる。
解く為のヒントも手順も示さずに、いきなり確率を答えさせている。(選択問題形式)
B型の質問紙による実験
被験者は文科系の大学一年生 231人
A型と同様に、標準的な3囚人問題の問題文に続けて、恩赦確率にばらつきのある変形3囚人問題の問題文に答えさせる。
まず多数回の試行を想像させ、標本空間の階層分割手順にそって条件に合う試行の数を計算させた上で確率を答えさせている。(選択問題形式)
A型と同様に、標準的な3囚人問題の問題文に続けて、恩赦確率にばらつきのある変形3囚人問題の問題文に答えさせる。
まず多数回の試行を想像させ、標本空間の階層分割手順にそって条件に合う試行の数を計算させた上で確率を答えさせている。(選択問題形式)
実験結果
B型の質問紙の場合、標準的な 3囚人問題で、正答率 64%、 変形 3囚人問題で、正答率 56% という結果になった。
得られた知見
多数回の試行を想像させると正答率が高い。
結論
3囚人問題の確率の錯覚の背後に重要な直感のメカニズムがあるわけではなく、単に事後確率の考え方を知らなかっただけのことだ。
※私の感想 :
確率の錯覚の原因は単に知識不足が原因だとする論文執筆者の仮説は、統計数学者も錯覚するという事実に反しているだろう。それを裏付けるように、論文執筆者が得た結論と真逆の結論を同じ実験データから導くことができる。
その1
その1
全員正解しそうな B型の標準的3囚人問題で、 確率を錯覚している割合が 19% まで落ちてはいるものの、 正答率が 64% 止まりであったので、 直感のメカニズムの重要性こそ、この実験結果から導くべきだろう。
その2
Shimojo, S., & Ichikawa, S. (1989).が、事前確率の比率を維持しながら事後確率を計算するヒューリスティク説を提唱している。 (彼らはこのヒューリスティクを「等比率の定理」と呼んでいる) A型の質問紙による変形 3囚人問題で最も多かった回答は、まさにこの「等比率の定理」に従っている。
Aaron, E. and Spivery, M. (1998).は、モンティ・ホール問題について同様な実験を行っている。報告された実験のあらましは次のとおり。使用された質問紙はいずれも挑戦者が扉Aを選んだケースで組み立てられている。
実験1
被験者はコーネル大学の学生 (度数で答えさせる質問紙に58人、 確率値で答えさせる質問紙に54人)
論文には質問紙の具体的な内容が掲載されていない。
switch すべしと答えた割合は、 度数型で21%、確率値型で18%
論文には質問紙の具体的な内容が掲載されていない。
switch すべしと答えた割合は、 度数型で21%、確率値型で18%
実験2
被験者はコーネル大学の学生 (度数で答えさせる質問紙に34人、 確率値で答えさせる質問紙に34人)
質問紙
質問紙
質問1: 扉Aに自動車がある度数または確率を質問している。質問2、 3は扉を代えて質問している。この質問だけ予め答えが書かれている。
質問4: 扉Aに自動車があるという条件でホストが扉Bを開ける度数または確率を質問している。質問5、 6は自動車がある扉を代えて質問している。
質問7: 挑戦者が扉Aを選んだという条件のみで、ホストが扉Bを開ける度数まはは確率を質問している。
質問8: 挑戦者が扉Aを選び、ホストが扉Bをあけたという条件で、扉Aに自動車がある度数または確率を質問している。質問9、 10は自動車がある扉を代えて質問している。
最後に stay すべきか、switch すべきか、質問している。
質問4: 扉Aに自動車があるという条件でホストが扉Bを開ける度数または確率を質問している。質問5、 6は自動車がある扉を代えて質問している。
質問7: 挑戦者が扉Aを選んだという条件のみで、ホストが扉Bを開ける度数まはは確率を質問している。
質問8: 挑戦者が扉Aを選び、ホストが扉Bをあけたという条件で、扉Aに自動車がある度数または確率を質問している。質問9、 10は自動車がある扉を代えて質問している。
最後に stay すべきか、switch すべきか、質問している。
switch すべしと答えた割合は、 度数型で29%、確率値型で12%
実験3
被験者はコーネル大学の学生 (度数で答えさせる質問紙に38人、 確率値で答えさせる質問紙に37人)
質問紙は実験2の質問紙の最初の6問に予め答えが書いてあるもの。
switch すべしと答えた割合は、 度数型で37%、確率値型で27%
質問紙は実験2の質問紙の最初の6問に予め答えが書いてあるもの。
switch すべしと答えた割合は、 度数型で37%、確率値型で27%
論文執筆者による考察
確率型の設問よりも、度数型の設問の方が、モンティ・ホール問題の背後にあるベイズ確率の原理の理解を助ける力がある。
※私の感想1 :
小林厚子 (1998). の実験のB型の標準的3囚人問題では、それぞれの囚人が恩赦の場合に看守が囚人Bが恩赦だと答える試行回数を答えさせてから、その合計を計算させているので、Aaron, E. and Spivery, M. (1998).の実験2の度数型の設問の順序と変わりない。 それにもかかわらず、 小林厚子 (1998). の実験のB型の標準的3囚人問題の正答率 64% に対し、Aaron, E. and Spivery, M. (1998).の実験2の度数型で switch と答えた割合が 29% にとどまったのは、後者の質問文の分かりづらさが原因かも知れない。
ためしに両者の質問文を並べると、後者の質問文の長さが際立ってくる。
前者の質問文
ためしに両者の質問文を並べると、後者の質問文の長さが際立ってくる。
前者の質問文
Aが恩赦になるとき、看守が「Bは処刑されるよ」と答える場合は何回あるだろうか?
後者の質問文
4) Of the rounds in the answer to question 1), the rounds in which the player chooses A in part 1 and the car is actually behind door A, in how many of those rounds will the host open door B in part 2 of the round?
※私の感想2 :
確率型では後で質問1、 2、 3の答えと質問4、 5、 6の答えを掛け算しなければならないため、度数型より難しくなっている。このように度数型と確率型の設問内容に本質的な違いがあるので、論文執筆者による考察のような結論は得られないのではないか?
場合分けをさせるような出題形式にすると正答率が高いという実験
Tubau, E. & Alonson, D. (2003). は場合分けの設問を含む出題形式にすると正答率が高いことを報告していて、彼らが実験結果から導いた結論はともかくも、実験方法は次のように大変興味深い。
第一実験
3つの窓を使ったコンピュータゲームを 45回行わせている。45回を始める前に switch が有利か、stick が有利か、それとも五分五分か、答えさせ、45回を終えた後で再び答えさせている。
結果をまとめた表から、次のようなことがわかる。
45回を始める前に switch 有利と回答した被験者で 45回終えた時点で五分五分と回答している者がいる。
45回を終えた時点で switch 有利と回答しなかった被験者も 45回の後の方になるほど switchする率が増している。
※私の感想 : この結果は人間が行動を決定するとき、認知 ( 外界をモデルに当てはめて認識すること ) ばかりでなく、ハトほどではないにしても、学習 (経験により有利な反応頻度が高まること) にもある程度頼っていることを示していると思う。
結果をまとめた表から、次のようなことがわかる。
45回を始める前に switch 有利と回答した被験者で 45回終えた時点で五分五分と回答している者がいる。
45回を終えた時点で switch 有利と回答しなかった被験者も 45回の後の方になるほど switchする率が増している。
※私の感想 : この結果は人間が行動を決定するとき、認知 ( 外界をモデルに当てはめて認識すること ) ばかりでなく、ハトほどではないにしても、学習 (経験により有利な反応頻度が高まること) にもある程度頼っていることを示していると思う。
第二実験
統制群 (標準的モンティ・ホール問題)
被験者が挑戦者役になり、実験者がホスト役になってゲームを行う。
check (小切手か?) の入った封筒(当り)1つと空の封筒(ハズレ)2つを使う。
ゲームの最中、封筒は挑戦者(被験者)とホスト(実験者)の間に立てられている。(そのための道具を使っている)
開始時、途中、終了時の3回、switch と stick のどちらがどのような理由で有利か、被験者に説明させる
check (小切手か?) の入った封筒(当り)1つと空の封筒(ハズレ)2つを使う。
ゲームの最中、封筒は挑戦者(被験者)とホスト(実験者)の間に立てられている。(そのための道具を使っている)
開始時、途中、終了時の3回、switch と stick のどちらがどのような理由で有利か、被験者に説明させる
実験群 (対戦型モンティ・ホール問題)
被験者二人でペアを組み、一人が意思決定者、他方が情報提供者の役をする。
エースのトランプカード(当り)1枚、エース以外のトランプカード(ハズレ)2枚を使う。
最初に意思決定者がカードを1枚選んで手に持つ(表側を見ない)。
残りを情報提供者が手に持つ(表側を見る)。
情報提供者は手持ちのハズレのカード1枚の表を意思決定者に見せる。
開始時、途中、終了時の3回、switch と stick のどちらがどのような理由で有利か、意思決定者と情報提供者それぞれに説明させる
エースのトランプカード(当り)1枚、エース以外のトランプカード(ハズレ)2枚を使う。
最初に意思決定者がカードを1枚選んで手に持つ(表側を見ない)。
残りを情報提供者が手に持つ(表側を見る)。
情報提供者は手持ちのハズレのカード1枚の表を意思決定者に見せる。
開始時、途中、終了時の3回、switch と stick のどちらがどのような理由で有利か、意思決定者と情報提供者それぞれに説明させる
結果の表やグラフを見ると、実験群の方が正しい判断と正しい説明をしている率が高い。
Tubau らは、実験群でカードを意思決定者の手の中と情報提供者の手の中の2つのグループに分けたことが正しいメンタルモデルの形成を助けたと述べている。
※私の感想 : 標本空間のような正しいメンタルモデルが形成されたのではなく、それぞれのカード群の中に確率が保存されるという錯覚的なメンタルモデルが形成されたのではないだろうか。
Tubau らは、実験群でカードを意思決定者の手の中と情報提供者の手の中の2つのグループに分けたことが正しいメンタルモデルの形成を助けたと述べている。
※私の感想 : 標本空間のような正しいメンタルモデルが形成されたのではなく、それぞれのカード群の中に確率が保存されるという錯覚的なメンタルモデルが形成されたのではないだろうか。
第三実験
場合分けを促すような設問にすると正しいメンタルモデルの形成を助けるだろうという仮説のもとに、モンティ・ホール問題に関する問題用紙を 3種類を作って、それぞれ何人かの学生に回答させて結果を比較している。
標準-ER条件 の問題用紙 (ER は explicit repesentation の頭文字)
標準-ER条件 の問題用紙 (ER は explicit repesentation の頭文字)
- ①ホスト、ゲスト、3つの封筒(1つだけ賞品あり)で構成される標準的なモンティ・ホール問題を説明する
- ②賞品の配置の場合分けを次のような解答用紙に書かせる
封筒1 封筒2 封筒3
可能性1
可能性2
可能性3
その他? - ③賞品の入った封筒を選ぶ確率 (設問1a) と、残りの封筒に賞品がある確率 (設問1b) を見積もらせる
- ④ 挑戦者が封筒1を選んだとして、上で場合分けしたそれぞれの可能性についてホストが開けるのはどの封筒か書かせる
- ⑤ ハズレの封筒が除かれた後に選んだ封筒の中に賞品がある確率 (設問2a) と、残りの封筒の中に賞品がある確率 (設問2b) を見積もらせる
- ⑥ switch が有利か、stick が有利か、それとも五分五分か、判断させ (設問3) 、その根拠を述べさせる (設問4)
対戦型-ER条件の問題用紙
- ① 第2実験で使った対戦型のモンティ・ホール問題を説明する
- ② 3枚のカードがダイヤのエース、ダイヤの7、ダイヤの8だとして、賞品の配置の場合分けを次のような解答用紙に書かせる
意思決定者 情報提供者
可能性1
可能性2
可能性3
その他? - ③ 意思決定者がエースを持っている確率 (設問1a) と、情報提供者がエースを持っている確率 (設問1b) を見積もらせる
- ④ 上で場合分けしたそれぞれの可能性について、情報提供者が示すのはどのカードか書かせる
- ⑤ 情報提供者がエース以外のカードを示した後に、意思決定者がエースを持っている確率 (設問2a) と、情報提供者がエースを持っている確率 (設問2b) を見積もらせる
- ⑥ switch が有利か、stick が有利か、それとも五分五分か判断させ (設問3) 、その根拠を述べさせる (設問4)
対戦型条件 の問題用紙
賞品の配置の場合分けの設問や、場合分けした場合のそれぞれで情報提供者がどのカードを示すかという設問が無いことを除いて、対戦型-ER条件の問題用紙と全く同じ問題用紙を使う。
実験結果
|
|
|
|
|
|---|---|---|---|
|
|
95% | 95% | 95% |
|
|
55% | 85% | 65% |
|
|
20% | 75% | 70% |
|
|
10% | 65% | 10% |
|
|
25% | 60% | 50% |
|
|
0% | 60% | 25% |
Tubau らは、対戦的条件で正答率が上がり、ER条件でさらに正答率が上がると述べている。
- ※私の感想 : 私は、標準型-ER と対戦型では、設問3 の低い正答率に比べて 設問4 の正答率がさらに低いことや、どの条件でも 設問1a や 設問2a に比べて 設問1b や 設問2b の正答率が低いことにも着目したい。
Tubau らは総論の中で対戦型でない標準的なモンティ・ホール問題の場合、賞品の配置の場合分けを書かせても効果がないと述べている。
補足:
- ※私の感想 : 標準-ER条件と対戦型-ER条件で結果が違うことの要因としては、場合分けの設問を出すタイミングが異なることの方が重要だと思う。
補足:
Tubau, E. & Alonson, D. (2003). の対戦型のモンティ・ホール問題は裏を見ただけでは区別できないトランプを使っているため、 特定事象による条件付確率あるいは事後確率の問題設定 をとることができないので、厳密にはモンティ・ホール問題ではなく、「扉を区別できないモンティ・ホール問題もどき」と呼ぶべきである。
通常の人間は 不特定事象による条件付確率あるいは事後確率の問題設定 や 非条件付確率の問題設定 をとることが困難であるから、 (少なくとも私がモンティ・ホール問題の初心者であった頃はそうだった) 対戦型のモンティ・ホール問題を心理学の実験材料とするということは、こうした問題設定,に誘う効果を実験していることになる。
通常の人間は 不特定事象による条件付確率あるいは事後確率の問題設定 や 非条件付確率の問題設定 をとることが困難であるから、 (少なくとも私がモンティ・ホール問題の初心者であった頃はそうだった) 対戦型のモンティ・ホール問題を心理学の実験材料とするということは、こうした問題設定,に誘う効果を実験していることになる。
問題の中に出てくるゲームの形式によって正答率が上がるという研究
扉の枚数を増やす実験
Page, S.E. (1998). の研究について、三好一英・服部環 (2009).が次のようにが紹介している。
ドアの枚数が3枚、10枚、100枚と増えるにつれて選択を変更する割合が増加する結果を報告しているらしい。ただし、サンプルサイズの点で検定力不足だそうだ。
ドアの枚数が3枚、10枚、100枚と増えるにつれて選択を変更する割合が増加する結果を報告しているらしい。ただし、サンプルサイズの点で検定力不足だそうだ。
対戦型にすると正答率が上がる (対戦型形式と標準型形式 参照)
先にあげたTubau, E. & Alonson, D. (2003). や、De Neys, W. & Vershueren, N. (2006). の実験結果から、対戦型にすると switch を選択する率が格段に上がることがわかる。
ボクサー型にすると正答率が上がる (ボクサー型ゲーム形式 参照)
Burns, B.D. & Wieths, M. (2004). によると、標準型に比べてボクサー型の方が正答率が高いらしい。
ベイズの定理を応用した計算方法を学習した者にも難しいことの実験
寺尾敦・伊藤朋子 (2010).では、くじ引き課題 (下記参照)に正答できるようになった学生に、変形3囚人問題 (恩赦確率が囚人ごとに異なる) を課題として与えて実験している。 尤度が記入されていない樹形図やルーレット図を提示したら誰も正答しなかったが、 尤度を明示した図を提示したら正答者が現れたと報告されている。
※くじ引き課題とは次のような課題
※くじ引き課題とは次のような課題
袋の中に白箱と黒箱が入っていて、袋の中に白箱と黒箱が入っている。
白箱の中には赤玉2個と青玉1個が入っていて、黒箱の中には赤玉1個と青玉1個が入っている。
袋の中の箱をランダムに選び、その箱の中からランダムに玉を一つ取り出したら、赤い玉だった場合に、白箱の中にあった確率を計算する。
白箱の中には赤玉2個と青玉1個が入っていて、黒箱の中には赤玉1個と青玉1個が入っている。
袋の中の箱をランダムに選び、その箱の中からランダムに玉を一つ取り出したら、赤い玉だった場合に、白箱の中にあった確率を計算する。
※ 私の感想 : くじ引き課題では、問題文自体にオッズ形式で尤度が書かれているということも効いているように思う。
3囚人問題の確率を直観的に計算する方法の種類別割合に関する実験
Shimojo, S., & Ichikawa, S. (1989). で、3囚人問題の確率を計算するときに利用する 「主観的定理」 (ヒューリスティクのようなもの) の種類を予備調査で調べ上げている。
そして、その準備のもとに、いくつかのバリエーションの問題文を使用した実験により 「主観的定理」 の使用割合を調べている。
問題文の種類
主観的定理の種類
実験の構成
実験結果
論文の中の図を見て次のようなことが (私には) わかった。
論文では実験の被験者自身が書いた確率判断の理由も分析している。 その中で次のことが私の関心を引いた。
そして、その準備のもとに、いくつかのバリエーションの問題文を使用した実験により 「主観的定理」 の使用割合を調べている。
問題文の種類
|
|
問題文の内容 |
|
|---|---|---|
|
|
囚人の恩赦確率はすべて 1/ 3 看守から囚人Bの名を聞いた囚人Aが自分の恩赦確率が |
1/3 |
|
|
問題文1 とほぼ同様 |
1/5 |
|
|
問題文1 とほぼ同様 ただし、看守が答えても新たな情報にならないことについての記述がない |
1/3 |
|
|
問題文2 とほぼ同様 ただし、看守が答えても新たな情報にならないことについての記述がない |
1/5 |
|
|
問題文1 とほぼ同様 |
1/3 |
|
|
問題文1 とほぼ同様 |
1/2 |
主観的定理の種類
| 主観的定理 | 内容 | 質問した囚人が恩赦である事後確率 |
|---|---|---|
| Number of cases |
|
|
| Constant ratio | 選択肢の確率比を保存して事後確率を計算 |
|
| Irrelevant, therefore invariant | 看守がいずれかの囚人の名を上げることは最初からわかっているので確率を変えない |
|
実験の構成
|
|
|
|
|---|---|---|
| 1 | 1 | 1 → 2 → 1 |
| 2 | 2 → 1 → 2 | |
| 2 | 1 | 3 → 4 → 3 |
| 2 | 4 → 3 → 4 | |
| 3 | 1 | 5 → 6 |
| 2 | 6→ 5 |
実験結果
論文の中の図を見て次のようなことが (私には) わかった。
|
|
|
提示順序 |
|
質問した囚人が恩赦になる事後確率に関する解答の分布 |
|---|---|---|---|---|
| 1 | 1 | 最初 |
|
1/2 と 1/3 が多くてほぼ同数 |
| 中間 |
|
1/4 と 1/3 が多い 1/3 が 1/4 の 2倍近い 1/3 と答えた被験者は 前の問題文で 1/2 と答えた被験者が多い |
||
| 最後 |
|
1回目の回答を引き継ぐ被験者が多い | ||
| 2 | 最初 |
|
1/4 と 1/3 が多くて同数 | |
| 中間 |
|
1/2 と 1/3 が多くてほぼ同数 1/2 と答えた被験者は 前の問題文で 1/3 と答えた被験者が多い |
||
| 最後 |
|
1回目の回答を引き継ぐ被験者が多い | ||
| 2 | 1 | 最初 |
|
1/3 と 1/2 が多い 1/2 が 1/3 の 2倍近い |
| 中間 |
|
1/4 と 1/3 が多い 1/3 と答えた被験者は 前の問題文で 1/2 と答えた被験者が多い |
||
| 最後 |
|
1回目の回答を引き継ぐ被験者が多い | ||
| 2 | 最初 |
|
1/3 が多い 実験1に比べて 1/4 が少なく 1/2 や 2/3 が多い |
|
| 中間 |
|
1/ 2 が 1/3 の 5倍近い 1/2 と答えた被験者は 前の問題文で 1/3 と答えた被験者が多い |
||
| 最後 |
|
1回目の回答を引き継ぐ被験者が多い |
||
| 3 | 1 | 最初 |
|
1/2 と 1/3 がほぼ同数 |
| 2番目 |
|
1回目の回答を引き継ぐ被験者が多い 1/3 から 1/2 に変わった被験者もいる |
||
| 2 | 最初 |
|
1/2 が 1/3 の2倍 | |
| 2番目 |
|
1/2 と 1/3 がほぼ同数 |
論文では実験の被験者自身が書いた確率判断の理由も分析している。 その中で次のことが私の関心を引いた。
実験1のグループ1で、最初の問題 (問題文1) で確率 1/2 と判断した被験者が"Constant ratio"定理と "Number of cases"定理のどちらを使ったか特定できないが、最後の問題 (問題文1) で確率 1/2 と判断した被験者は "Constant ratio"定理を明示的に理由としている。
問題文2 で確率 1/3 と判断した被験者は "Irrelevant, therefore invariant"定理を使っている。
問題文2 で確率 1/3 と判断した被験者は "Irrelevant, therefore invariant"定理を使っている。
私の感想
問題文3 で 1/2 と回答する被験者が実験1 にくらべて実験2 に多い理由や、問題文6 で 1/2 と回答する被験者が実験3 のグループ1 に比べてグループ2 に多い理由を知りたい。
3囚人問題の尤度を被験者自らに指定させた実験
囚人A, B, C の恩赦確率がそれぞれ 1/3, 1/6, 1/2 になるようなルーレットで恩赦になる囚人が決まる。
囚人Aは各囚人の恩赦確率を知っている。
Known 群の被験者に出した「変形3囚人問題」では、看守も各囚人の恩赦確率を知っている。
Unknown 群の被験者に出した「変形3囚人問題」では、看守は各囚人の恩赦確率を知らない。
囚人Aは各囚人の恩赦確率を知っている。
Known 群の被験者に出した「変形3囚人問題」では、看守も各囚人の恩赦確率を知っている。
Unknown 群の被験者に出した「変形3囚人問題」では、看守は各囚人の恩赦確率を知らない。
各グループの被験者に出した質問
質問1 ~ 4 は看守がBが処刑されると答えたという条件での質問。
質問5 ~ 8 は看守がCが処刑されると答えたという条件での質問。
質問1, 5 は 囚人A の恩赦確率を問う。
質問2, 6 は尤度 (囚人Aが恩赦のときに看守がBと答える確率とCと答える確率) を問う。
質問3, 7 は看守が答えた後の囚人Aが恩赦の事後確率と事前確率の比を問う。
質問4, 8 は囚人Aが恩赦の事後確率を問う。
質問5 ~ 8 は看守がCが処刑されると答えたという条件での質問。
質問1, 5 は 囚人A の恩赦確率を問う。
質問2, 6 は尤度 (囚人Aが恩赦のときに看守がBと答える確率とCと答える確率) を問う。
質問3, 7 は看守が答えた後の囚人Aが恩赦の事後確率と事前確率の比を問う。
質問4, 8 は囚人Aが恩赦の事後確率を問う。
この実験の結果、次のようなことが判明した。
- ◇被験者自らに尤度を想定させたにも関わらず、自分が想定した尤度を使わずに囚人Aが恩赦になる事後確率を推定していた。
- ◇大部分の被験者は Shimojo, S., & Ichikawa, S. (1989). の言うところの、'Constant ratio' 主観的定理で計算した。
- ◇各囚人の恩赦確率を看守が知っている条件でも、囚人Aに情報を与えない尤度
( P(B処刑と看守が告げる| A恩赦) = 3/4 ) を想定する被験者は増えなかった。
なぜ、マンモグラフィ-のガン罹患確率錯覚では基準率が無視され、 3囚人問題では被験者自ら尤度を想定しても尤度が無視されるのか興味がわく。
3/4 という半端な尤度を想定した非権者が少なからずいたのは、囚人B, C の恩赦確率の比1 : 3 を反映しているのだろう。
3/4 という半端な尤度を想定した非権者が少なからずいたのは、囚人B, C の恩赦確率の比
いったん標本空間を分割した後では事象の刈り込みしかできなくなるという説の実験
Fox, C.R. & Levav, J. (2004). では、 人間が条件付き確率を計算するとき、 "Partition → Edit → Count"という手順を無意識にとるという説を提唱している。
Partition と標本空間を分割することであり、 Edit とは証拠事象によって標本空間の刈り込みを行うことであり、 Count とは結果の条件付き確率を計算することである。
このモデルを検証するために、次のような実験を行っている。
研究 1 ( Editing に影響するような条件を操作した実験 )
Partition と標本空間を分割することであり、 Edit とは証拠事象によって標本空間の刈り込みを行うことであり、 Count とは結果の条件付き確率を計算することである。
このモデルを検証するために、次のような実験を行っている。
研究 1 ( Editing に影響するような条件を操作した実験 )
研究 1A
5枚のカードを使った対戦型モンティ・ホール問題 ( 対戦型形式と標準型形式 参照) のゲームを大学生を挑戦者とし、実験者がホストになって行っている。
挑戦者の手に 2枚、ホスト(実験者) の手に3 枚のカードを持つ。
被験者によってホストが、 はずれカードをめくらない、 はずれカードを 1枚だけめくる、 はずれカードを 2枚めくる、の3パターンのどれかを行う。
実験の結果、モデルが予想する通り、switch して当たる確率の判断が残ったカードの枚数で変わった。
挑戦者の手に 2枚、ホスト(実験者) の手に3 枚のカードを持つ。
被験者によってホストが、 はずれカードをめくらない、 はずれカードを 1枚だけめくる、 はずれカードを 2枚めくる、の3パターンのどれかを行う。
実験の結果、モデルが予想する通り、switch して当たる確率の判断が残ったカードの枚数で変わった。
研究 1B
研究 1A と同じゲームを行う。
挑戦者によってホストが、 はずれカードを2枚めくる、 はずれカードを2枚指し示す、の2パターンのどちらかを行う。
実験の結果、モデルが予想する通り、はずれカードを指し示すパターンで正答率が上がった。
挑戦者によってホストが、 はずれカードを2枚めくる、 はずれカードを2枚指し示す、の2パターンのどちらかを行う。
実験の結果、モデルが予想する通り、はずれカードを指し示すパターンで正答率が上がった。
研究 2 ( Partitioning に影響するような条件を操作した実験 )
研究 2A
製薬会社3社の抗がん剤をFDAが評価するという設定の問題文で、次の2種類の問題文を使っている。
【最優秀型】の問題文
【最優秀型】の問題文
FDAは 3社の抗がん剤のうち最優秀な製品を見つけようとしている。
A社の製品がC社の製品より優秀だとわかったら、A社の製品が最優秀である確率は?
A社の製品がC社の製品より優秀だとわかったら、A社の製品が最優秀である確率は?
【序列型】の問題文
FDAは 3社の製品の序列を判断しようとしている。
A社の製品がC社の製品より優秀だとわかったら、A社の製品がB社の製品にも優る確率は?
A社の製品がC社の製品より優秀だとわかったら、A社の製品がB社の製品にも優る確率は?
実験の結果、モデルが予想する通り、序列型の問題文で正答率が上がった。
研究 2B
「スミスさんの子供たち」 問題を実験材料としている。スミスさんの子供は二人で、男の子を含んでいる。
【最初に一人の子供を意識させる型】の問題文
【最初に一人の子供を意識させる型】の問題文
少なくとも一人は男の子だと聞いた。もう一人も男の子である確率は?
【二人を一組として意識させる型】の問題文
女の子が二人ということはないと聞いた。二人とも男の子である確率は?
実験の結果、モデルが予想する通り、二人を一組として意識させる型の問題文で正答率が上がった。
研究 2C
両面赤、赤面と白面、両面白、の3種類のカードが 1枚ずつ入っている帽子の中から、 目をつむって1枚を取出してテーブルに置いたら表が赤かったとき、裏も赤い確率を予想させる実験で、次の 2種類の問題文を使っている。
【カード単位分割型】の問題文
【カード単位分割型】の問題文
3枚のカードを、赤-赤、赤-白、白-白、と名付ける
【カードの面単位分割型】の問題文
6面を、赤1 、赤2 、赤3 、白1 、白2 、白3、と名付ける。
赤3 と白1 が同じカードである。
赤3 と白1 が同じカードである。
実験の結果、モデルが予想する通り、カードの面単位分割型の問題文で正答率が上がった。
研究 3 ( 標本空間の分割と個体が対応していることの影響に関する実験)
次のような問題文で実験を行っている。
A社の部長は二人とも強い、B社の部長は一人だけ強い、C社の部長は二人とも弱い。
【会社単位分割型】の問題文
【会社単位分割型】の問題文
キャサリンは強い部長だ。
キャサリンの会社のもう一人の部長が強い確率は?
キャサリンの会社のもう一人の部長が強い確率は?
【部長単位分割型】の問題文
キャサリンは強い部長だ。
キャサリンがA社の強い部長の一人である確率は?
キャサリンがA社の強い部長の一人である確率は?
各々の部長は強いか弱いかどちらかなので、;標本空間の分割と個体(部長)が対応している。 このような場合、Brase, G. L., Cosmides, L., & Tooby, J. (1998).が提唱する仮説によると、会社単位分割型でも誤答が少なくなりそうであるが、、実験の結果は否定的であった。
研究 4 ( 結果に影響する情報を増やした場合の影響に関する実験 )
ドジャースとメッツの試合を題材にした問題文で実験を行っている。
私の感想
Shimojo, S., & Ichikawa, S. (1989). が見出した主観的定理を、この論文の提唱する "Partition → Edit → Count" モデルと組み合わせると面白い。
たとえば、 Constant ratio theorem という主観的定理なら、Edit の働きとして説明できそうだ。
Irrelevant, therefore invariant という主観的定理なら、Edit が省略されることで説明できる。
開ける扉を特定しないこと、視点の変更、および場合分けの促しの組み合わせに関する実験
Krauss, Stefan and Wang, X. T. (2003). . の実験1 と実験2 は次の3種類のヒントの組み合わせ方が正答率や問題の理解に与える影響を調べるための実験である。
ちなみに、被験者に与える問題文の冒頭のゲームのルールの説明の中で、 モンティ・ホールが当たりの扉や挑戦者が選んだ扉を開けないことを明記している。
ベルリン大で行われた実験1とサウスダコタ大で行われた実験2の結果を一つの表にまとめると次のようになる。
- モンティ・ホールが開ける扉を扉3に限定しないことが正当率を上げる効果 (「少ないは多い」)
- モンティ・ホールになったつもりで考えさせると正答率が上がる効果(「視点変更」)
- メンタルモデルを思い浮かべることを促すことが正当率を上げる効果(「メンタルモデル」)
- 場合の数を数えるよう促すことが正当率を上げる効果(「頻度」)
ちなみに、被験者に与える問題文の冒頭のゲームのルールの説明の中で、 モンティ・ホールが当たりの扉や挑戦者が選んだ扉を開けないことを明記している。
ベルリン大で行われた実験1とサウスダコタ大で行われた実験2の結果を一つの表にまとめると次のようになる。
| 正答率を上げたり問題の構造を理解させたりするための操作 | パラメータ |
統制タイプ の問題文 実験1 |
統制タイプ の問題文 実験2 |
1Dタイプ の問題文 実験1 |
1D+F タイプ の問題文 実験2 |
1D+P タイプ の問題文 実験2 |
GIタイプ の問題文 実験1 |
GIタイプ の問題文 実験2 |
|---|---|---|---|---|---|---|---|---|
| 被験者数 | 67人 | 35人 | 34人 | 34人 | 34人 | 34人 | 34人 | |
| 少ないは多い | 特定する扉の数と種類 |
選んだ扉 開けた扉 |
選んだ扉 開けた扉 |
選んだ扉 | 選んだ扉 | 自動車の扉 | 選んだ扉 | 自動車の扉 |
| 視点の変更 | 誰の視点で考えさせるか | 挑戦者 | 挑戦者 | 挑戦者 | 挑戦者 | モンティ・ホール | モンティ・ホール | モンティ・ホール |
|
頻度シミュレーション 「頻度」と「メンタルモデル」を合体させたもの |
メンタルモデルに添って頻度の質問をするか 注参照 |
しない | しない | しない | する | しない | する | する |
| たまたま交換を選んだ割合 | 16% | 17% | 15% | 6% | 3% | 9% | 6% | |
| 正しい直感によって交換を選んだ割合 | 2% | 6% | 12% | 12% | 17% | 12% | 12% | |
| 理由づけも正しい割合 | 3% | 0% | 12% | 9% | 9% | 38% | 32% | |
| 計 | 21% | 23% | 38% | 26% | 29% | 59% | 50% |
1D とは One Door を意味し、 GI とは Guided Intuition (案内付の直感) を意味している。
この論文で 「頻度」と呼んでいるものは 「場合の数」 のことである。
メンタルモデルとは、扉1に自動車がある、扉2に自動車がある、扉3に自動車がある、といった3つの可能性をイメージすることである。
頻度の質問とは、3つの可能性のうち交換で勝つ可能性の数と、交換しないで勝つ可能性の数を答えさせるものである。
実験結果の執筆者による考察から抜粋すると次のようになる。
- 4つの操作全てを伴う GI (案内付の直感) タイプの問題文にすると、switch を選択させる強い効果がある。
- 選んだ扉の方を特定するか、自動車のある扉の方を特定するかで、結果に目立った差がない。
- 統制タイプの問題文で switch を選んだ割合が 22% という高い値であるが、数学的構造を理解した割合は非常に小さい。
- 頻度シミュレーション単独や視点変更単独では効果が薄いが、 それらを組み合わせると単独での効果の和を上回る高い効果を示した。
- 頻度シミュレーションを活かすには 「少ないは多い」 も必要。 開ける扉が特定されていないからこそ、頻度を数えることができる。 それらを組み合わせると単独での効果の和を上回る高い効果を示した。
- 頻度シミュレーションと視点変更が組み合わさって始めて効果を持つことは、単一の要因の操作の結果から誤った認知心理学的結論に至るおそれを示している。
- 他のベイズ問題でも、視点変更の効果が重要かも知れない。
- 「少ないは多い」 と 「頻度シミュレーション」 (「頻度」 + 「メンタルモデル」) の組み合わせは、 とりも直さず、 不特定事象による条件付確率あるいは事後確率の問題設定 、あるいは 非条件付確率の問題設定 に他ならない。
この論文で有効性の確認された問題文の操作とは、
考え方は単純でも尤度の計算が必要な条件付き確率の問題設定から、
思いつくのは容易でないが、ひとたび教えてもらえば場合の数だけで解ける問題設定に
乗り換えさせる操作なのだろう。
- Tubau, E. & Alonson, D. (2003). の対戦型モンティ・ホール問題や、 Burns, B.D. & Wieths, M. (2004). のボクサー型モンティ・ホール問題で正答率が上がったことと、 この論文のやり方で正答率が上がったことの背後に、 同一の心理メカニズムがあるかも知れない。
この論文の研究目的は先行研究のテクニックの組合わせに関するものなので当然と言えば当然である。
- この論文の実験で頻度シミュレーションで正答率が上がった理由に関する Burns, B.D. & Wieths, M. (2004). の中のコメントが興味深い。
モンティ・ホール問題解決方法の転移に関する実験
Krauss, Stefan and Wang, X. T. (2003). . の実験3 は、 モンティ・ホール問題に対して、どのような解き方を説明して訓練させると、類似問題に効果が転移するか、 という観点で実験を行っている。
実験3 で使われた解き方の訓練方法の種類
これらの道具立てで、次のような順序で実験を行っている。
(1) [通常のモンティ・ホール問題を解かせる。
(2) 各被験者に、いずれか一つの方法で訓練を行う。
(3) 各被験者に、応用問題全種類を解かせる。
実験結果に対する考察の中では、次の2点が私の興味を引いた。
実験3 で使われた解き方の訓練方法の種類
- 頻度シミュレーション 扉が横に並んだ図を利用して場合の数を数える
- メンタルモデルによる訓練 メンタルモデルの表を利用して場合の数を数える
- ベイズルールによる訓練 ベイズルールを利用
- 扉の数は、 ヤギ 1 , 自動車 2
- 扉の数は、 ヤギ 2 , 自動車 2 で、 開ける扉の数は、 ヤギ 1 , 自動車 1
私の注: このパターンの場合、 「交換してもしなくても同じ」 という回答が正解になる。 - 3囚人問題
- Dunker Tumor 問題 (訓練の効果が最初から期待されない種類の問題)
|
メンタル モデル |
扉1 選んだ扉 |
扉2 | 扉3 |
|---|---|---|---|
| 1 | 自動車 | 開ける | |
| 2 | 自動車 | 開ける | |
| 3 | 自動車 | 開ける | |
| 4 | 自動車 | 開ける | |
| 5 | 開ける | 自動車 | |
| 6 | 開ける | 自動車 |
これらの道具立てで、次のような順序で実験を行っている。
(1) [通常のモンティ・ホール問題を解かせる。
(2) 各被験者に、いずれか一つの方法で訓練を行う。
(3) 各被験者に、応用問題全種類を解かせる。
実験結果に対する考察の中では、次の2点が私の興味を引いた。
- ベイズルールは手元に公式を書いた紙がないと応用が難しい。
- 頻度シミュレーション群と、メンタルモデル群の両方で、ヤギ2, 自動車2 の問題の方が 3囚人問題より解きやすい。 この結果は、
「訓練で使った問題に内容が似ていても答えが違っている問題より、内容が似ていなくても答えが同型の問題の方が、 訓練で学んだ解き方を応用しやすい」
という Reed, S. K.(1993). による結果に反するので興味深い。 3囚人問題に応用するためには、扉を人に対応付ける必要があるためかも知れない。
「因果推論」(Causal Inference) の困難さが関係しているという説の実験
コライダー構造に関する意識に誘うような問題形式にした実験
Burns, B.D. & Wieths, M. (2004). では、モンティ・ホール問題の因果構造がコライダー構造であることに着目して、因果関係がコライダー構造になっていることに気づかせるような問題形式を工夫して実験している。
ちなみに、モンティ・ホール問題のコライダー構造は次のようになっている。
(賞品の配置) → (ホストが開ける扉) ← (挑戦者が選んだ扉)
以下は、論文の記述をベースにしつつ、表現を短くしたり、抜粋したりして、私なりに整理したものである。
実験1
ちなみに、モンティ・ホール問題のコライダー構造は次のようになっている。
以下は、論文の記述をベースにしつつ、表現を短くしたり、抜粋したりして、私なりに整理したものである。
実験1
次の四つのバージョンのうちの一つを被験者に解かせる
表2
- ボクサーバージョン
3人のボクサーのうち一人は他の誰よりも強い
ゲームの挑戦者が選んだボクサーが勝ち残ると、その挑戦者の勝ち
ゲームの挑戦者が最初に選んだボクサー以外の二人が最初の試合を行う
ゲームの挑戦者は最後の試合の前にボクサーをswitchできる
私の注:試合が公正で完全に競争的なコンテキストになっている - レスラーバージョン
レスラーの組み合わせごとに勝者が事前に決まっている点がボクサーバージョンと異なる
ボクサーバージョンより試合の公正さが失われている
私の注:プロボクシングと異なり、プロレスリングはシナリオのあるショーである。 - レスラーと扉バージョン
それぞれのレスラーに扉が割り当てられている
賞品のある扉は最強のレスラー割り当てられていて、レスラーが負けるとその扉が開けられる
私の注:このような構造にすると、レスラーバージョンよりさらに正答率が下がると、論文執筆者は予想している - 扉バージョン
それぞれのレスラーに扉が割り当てられている
賞品のある扉は最強のレスラー割り当てられている
レスラーの試合で、レスリングを行わずに、単に叫びあうだけで、そうしていると興行主が彼らに割り当てられた扉の一つを開ける
私の注:完全に非競争的なコンテキストであり、レスラーの存在を無視すれば標準的なモンティ・ホール問題と変わらない
表2
| 扉 | レスラーと扉 | レスラー | ボクサー | |
|---|---|---|---|---|
| switch を選んだ | 15% | 37% | 30% | 51% |
| 正確に確率を見積もった | 2% | 4% | 10% | 14% |
実験2
選択肢の数(3、32、128) と文脈(競争的、非競争的)の組み合わせによる 6パターンのうちの一つを被験者に与える。
表3 (論文中の表3 を一つにまとめたもの)
私の注:
競争的コンテキストでも、選択肢の数を増やすことの効果が表れているので、競争的コンテキストにすることの効果と、選択肢の数を増やすことの効果が、別個のメカニズムによるものだということがわかる。
- 競争的問題文
選択肢の数だけいるテニスの競技者の中から一人を被験者に選ばせ、その競技者Xが試合前に失格と判定されたとする。
ファイナルマッチの2人が残った時点でXの失格判定が誤りだと分かったので、ファイナルマッチの勝者YとXで優勝を争う。
次の二つの文のどちらに同意するか問う。
• 二人の競技者が残ったということは、Xが勝ちそうか、Yが勝ちそうか、に影響しない。
• Xと争うべく、Yが勝ち進んだプロセスは、どちらが勝ちそうかの判定に影響する。 - 非競争的問題文
被験者が地方TV局番組に出演しているつもりにさせる。
選択肢の数だけある箱の一つに賞品がある。
被験者は一つの箱Xを選ぶ。
ホストは残りの箱から二つを取り出してから、その中のハズレの一つを開けるという所作を繰り返して、X を含めて二つの箱が残った。
次の二つの文のどちらに同意するか問う。
• 二つの箱が最後に残ったということは、Xが当たりそうか、Yが当たりそうか、に影響しない。
• どの箱が当たりかを知っている者に開けられずにYが残ったプロセスは、Xと比較して当りそうかの判定に影響する。
表3 (論文中の表3 を一つにまとめたもの)
|
選択肢 3個 |
選択肢 32個 |
選択肢 128個 |
全体 | ||
|---|---|---|---|---|---|
| switch を選んだ率 | 競争的 | 36% | 68% | 77% | 62% |
| 非競争的 | 15% | 46% | 46% | 36% | |
| 影響すると回答 | 競争的 | 50% | 73% | 78% | 68% |
| 非競争的 | 27% | 44% | 55% | 42% |
私の注:
競争的コンテキストでも、選択肢の数を増やすことの効果が表れているので、競争的コンテキストにすることの効果と、選択肢の数を増やすことの効果が、別個のメカニズムによるものだということがわかる。
実験3
ボクサーバージョンか扉バージョンのどちらかを被験者に与えて swich か stay か選ばせてから、以下の質問に答えさせる。
Krauss, Stefan and Wang, X. T. (2003). で頻度型の問題文で成績がよくなったと報告されていることと矛盾するように見えることについて、この論文では、Krauss, Stefan and Wang, X. T. (2003). の実験で使った質問の選択肢が少ないことなどに起因するとしている。 しかし、頻度の意味が異なることの方が重要だと私には思える。 この論文の頻度質問には、架空の9人が登場して、ややこしい。
- 頻度質問
架空の9人の人間が同じ問題を与えられたとして、
9人全員が switch を選んだ場合、9人のうちの何人が賞品を得るか?
9人全員が stay を選んだ場合、9人のうちの何人が賞品を得るか? - Nonrandomness 質問
最初の選択肢が除かれるプロセスのランダム度合を、0 (完全にランダム)から 6 (完全に非ランダム) までのスケールで評価させる - Counterfactual 質問
開けた扉Aにたまたま賞品がなかったが、興行師はランダムに扉を開けていたとしたら、あるいは、最初の試合で誰が勝つかはランダムだったとしたら、そういう知識は、switch か stay かの被験者自身による選択や、架空の9人のうち何人が当たるかに影響するか? - Process 質問
A、B、C のうち、一番正しそうな文章を選ばせる
A 最初の選択肢が除かれるに至るアクションは、swithc や stay で当たる確からしさに影響しない
B 最初の選択肢が除かれるに至るアクションは、swithc で当たる確からしさを増す
C 最初の選択肢が除かれるに至るアクションは、stay で当たる確からしさを増す
D どれも正しくない
- 「Couterfactual 質問」 の回答と switch 率との関係に関する結果 (表4) 、および「Process 質問」 の回答と switch 率との関係に関する結果 (表5) から、仮説1が支持されたとしている。 (表4 と 表5 の引用は省略します)
- 頻度質問について
switch を選びかつ頻度質問に 6/9 と正答した率が、競争的コンテキストでわずか14%、非競争的コンテキストで2% だったことから、頻度質問を加えても成績が向上しなかった。 - Counterfactual 質問について
switch を選んだ被験者のうち、競争的コンテキストで 75% 、 非競争的コンテキストで 63% が Couterfactual 質問に YES や MAYBE と回答したことに着目している。 - Process 質問について
stay を選んだ中で 「影響しない」 と回答した割合が非競争的コンテキストで高いことに着目して、仮説2 と 仮説4 ( 「コライダー原理の影響を理解した者は標準的モンティ・ホール問題でも成績がよい」 ) が支持されたとしている。 - Nonrandomness 質問について
非競争的コンテキストで平均 4.2 、競争的コンテキストで平均 3.7 となったが、 非競争的の方が低い理由はよくわからないとしている。 - 分散分析を行ったところ、Nonrandomness 質問の答えと Counterfactual 質問の答えに関連性が見いだせなかったとしている。
Krauss, Stefan and Wang, X. T. (2003). で頻度型の問題文で成績がよくなったと報告されていることと矛盾するように見えることについて、この論文では、Krauss, Stefan and Wang, X. T. (2003). の実験で使った質問の選択肢が少ないことなどに起因するとしている。 しかし、頻度の意味が異なることの方が重要だと私には思える。 この論文の頻度質問には、架空の9人が登場して、ややこしい。
実験4
Transfer 条件での質問の進め方
表7
- 実験3 のボクサーバージョンの問題文を与え、stay か switch か選ばせる。
- stay と switch のそれぞれの当たる頻度を評価させる
- 下記の文と質問を与える
ボクサーC が最強である確率は 2/3 なので、switch した方が当たりやすいことは実験すればすぐにわかる。
ボクサーC については、最初の試合で勝ったという知識が得られたが、ボクサーB については何も知識が得られていないので、ボクサーC が B に勝る可能性が高い。
ボクサーC にswitch した方が本当によいと確信しているか正直に答えよ - 因果関係の構造やコライダー原理が陽に示された例と、それに関する質問を与える
ボクサーC が勝つことによってボクサーC に関する知識が増すのは最初の試合で勝つボクサーという単一の結果が、どのボクサーをあなたが選んだかと、どのボクサーが最強か、という二つの原因に起因しているからである。
別の例で説明しよう。
ベートーベン大学には SAT (大学進学適正試験) で高得点をとるか、音楽の才能がなければ入れないので、ベートーベン大学の学生の SAT の得点と音楽の才能に負の相関関係がある。
つまりベートーベン大学に入れたという単一の結果に、 SATが高得点だということと、音楽の才能があるということの、 二つの原因が関係している。
あなたは音楽家を探していて、三人の候補者がいるが、オーディションをする時間がない。
ある理由から、二人の候補の SAT の高低を知った。(得点そのものは不明)
候補たちがベートーベン大学の学生だった場合、どの候補を選ぶべきか?
A SATの高い方
B SATの低い方
C SATの分からない方
D 三人とも同等
この状況はボクサー問題と類似しているか? - 実験3 の扉バージョンを与えて、下記の質問に答えさせる。
stay か switch か
「頻度質問」
「Counterfactual 質問」
- 実験3 の扉バージョンを与えて、下記の質問に答えさせる。
stay か switch か
「頻度質問」
「Counterfactual 質問」
- 表6で Transfer 条件の方が扉バージョンでの成績がよいことに着目している。
- 頻度質問について
Transfer 条件での頻度質問の正答率13/103 が Nontransfer での正答率6/103 に優ったが統計的に有意でないとしている。 - Counterfactual 質問について
YES または MAYBE と回答した被験者のうち、stay 47%、switch 76% であったことが仮説4 を支持しているとしている。 - 表7で、Transfer 条件の方が YESまたはMAYBEと回答した割合が高いことに着目している。
- Transfer 条件での訓練タスクについて
表8から、扉バージョンでの成績が三つの訓練タスクによって上がったと言えるが、 どの訓練タスクが効いたのかはわからないとしている。
| Nontransfer | Transfer | Transfer | |
|---|---|---|---|
| 扉バージョン | ボクサーバージョン | 扉バージョン | |
| switch を選んだ率 | 12% | 44% | 36% |
表7
|
Counterfactual 質問に対する 解答 |
Transfer | Nontransfer |
|---|---|---|
| YES | 26人 | 14人 |
| MAYBE | 37人 | 34人 |
| NO | 40人 | 52人 |
| 計 | 103人 | 100人 |
全体を通しての感想 1
この論文の文体や語彙は私には難読だった。 もしかしたら実験に使った問題文もそうだったのではないか? 論文に実験に使った問題文そのものが書かれていないのが残念。
全体を通しての感想 2
コライダー原理に気づくとどのようなメンタルモデルが形成されるか不明なため、正答した被験者たちが数学的に正当なメンタルモデルにもとづいて回答したかどうか疑わしい。
挑戦者が選んだ扉と当たりの扉の両方がホストが開ける扉の決定に関与するというモンティ・ホール問題のコライダー原理は、見方を変えると、挑戦者が選ばなかった二つの扉と当たりの扉がホストが開ける扉の決定に関与しているというコライダー原理でもある。
そのため、コライダー原理にのっとって仮説事象と証拠事象のネットワークを意識して問題を解くのでなく、 確率継承説 につながるようなメンタルモデルが形成されたのかもしれないからである。
モンティ・ホール問題に正答するか否かとワーキングメモリー(WM)の大小が関係していることを示した実験
De Neys, W. & Vershueren, N. (2006). はモンティ・ホール問題の正答するか否かとワーキングメモリーの大小が関係していると報告している。
実験1 (標準的なモンティ・ホール問題で実験)
実験1 (標準的なモンティ・ホール問題で実験)
ワーキングメモリーの大小は、Gospanスコアを使って調べている。算数の課題をやりながら同時に単語を何個まで覚えられるかというスコアである。
モンティ・ホール問題の問題文はKrauss, Stefan and Wang, X. T. (2003). が実験で使った問題文をベースにしたもので、賞品の配置がランダムであることと、ホストが賞品の配置を知っていることを明記している。
実験の結果、5.2% の被験者が switch と正答していて、正答者のGospanスコアの平均値は 38.08、非正答者のGospanスコアの平均値は 31.94 である。
モンティ・ホール問題の問題文はKrauss, Stefan and Wang, X. T. (2003). が実験で使った問題文をベースにしたもので、賞品の配置がランダムであることと、ホストが賞品の配置を知っていることを明記している。
実験の結果、5.2% の被験者が switch と正答していて、正答者のGospanスコアの平均値は 38.08、非正答者のGospanスコアの平均値は 31.94 である。
実験2 (対戦型のモンティ・ホール問題で実験)
ワーキングメモリーの評価方法は実験1と同様
モンティ・ホール問題の問題文は Tubau, E. & Alonson, D. (2003). の第二実験の対戦型モンティ・ホール問題を応用したもので、トランプカードの替わりにカップとボールを用いている。
カップをテーブルか何かの上にならべているようなので、並んだ順でカップを区別することができるのであれば、 特定事象による条件付確率あるいは事後確率の問題設定 をとることができる。
実験の結果、23% の被験者が switch と正答していて、正答者のGospanスコアの平均値は 39.97、非正答者のGospanスコアの平均値は 35.08 である。
モンティ・ホール問題の問題文は Tubau, E. & Alonson, D. (2003). の第二実験の対戦型モンティ・ホール問題を応用したもので、トランプカードの替わりにカップとボールを用いている。
カップをテーブルか何かの上にならべているようなので、並んだ順でカップを区別することができるのであれば、 特定事象による条件付確率あるいは事後確率の問題設定 をとることができる。
実験の結果、23% の被験者が switch と正答していて、正答者のGospanスコアの平均値は 39.97、非正答者のGospanスコアの平均値は 35.08 である。
実験3 (ワーキングメモリの負荷を高めて実験)
Miyake, A., Friedman, N. P., Rettinger, D. A., Shah, P., Hegarty,M. (2001). を参考にして、ワーキングメモリーに負荷を加えて実験している。
3×3のマトリックスに書かれた黒丸の配置を覚える課題によりワーキングメモリに負荷を加えている。黒丸三つを一列に並べたパターンが低負荷用で、黒丸四つを並べたものが高負荷用。
モンティ・ホール問題の問題文は実験2 と同一。
実験の結果、低負荷群の21.6% が正答できたが、高負荷群の 7.8% しか正答できなかった。
3×3のマトリックスに書かれた黒丸の配置を覚える課題によりワーキングメモリに負荷を加えている。黒丸三つを一列に並べたパターンが低負荷用で、黒丸四つを並べたものが高負荷用。
モンティ・ホール問題の問題文は実験2 と同一。
実験の結果、低負荷群の21.6% が正答できたが、高負荷群の 7.8% しか正答できなかった。
因果関係が推測しやすい問題文を使った実験
モンティ・ホール問題が難しいのは、司会者がCのドアを開けたのは何故かという因果的な推論を大部分の解答者が行わないためである
【実験に使った問題文】
「司会者がCのドアを開けたのは、Bのドアのうしろに新車があるからではないか」という因果推定がなされやすいように変更した問題文
【実験結果】
予測どおり正答率が上がった。
モンティ・ホール問題に対する素人解法による解答や説明がちまたにあふれている。
その理由として次のことが考えられる。
①数学的な説明を理解しても納得できない
その理由として次のことが考えられる。
①数学的な説明を理解しても納得できない
元来、「非条件付確率の問題設定」や、「不特定事象による条件付確率あるいは事後確率の問題設定 」での解答は簡単なものである。
モンティ・ホール問題なら
3囚人問題なら
しかしいくら頭で理解しても心で納得できないために、これらの説明が不十分なのだと錯覚してしまい、もっとましな説明があるはずだと、あれこれ考え始めるのである。
私も「もっと分りやすい説明があるのではないか」と、自分なりの素人解法を探しあぐねた一人である。
モンティ・ホール問題なら
「挑戦者が選ばなかった扉が当たりの確率 2/3 が switch して賞品を得る確率である」
と述べれば充分である。3囚人問題なら
「質問した囚人Aが恩赦でない確率 2/3 が看守が名を上げなかった残りの囚人が恩赦である確率である」
と述べれば充分である。しかしいくら頭で理解しても心で納得できないために、これらの説明が不十分なのだと錯覚してしまい、もっとましな説明があるはずだと、あれこれ考え始めるのである。
私も「もっと分りやすい説明があるのではないか」と、自分なりの素人解法を探しあぐねた一人である。
②標準仮定の下では素朴な等確率の場合分けで解くことができる。
標準仮定の下では 「非条件付確率の問題設定」 や、「不特定事象による条件付確率あるいは事後確率の問題設定 」 の場合に等確率の場合分けが可能であるので、数学的な確率概念に疎い人でも色々な説明を考え出すことが出来る。
人気が薄いせいか、3囚人問題の素人解法や素人説明はあまり見かけない。
ちまたで見かける「非条件付確率の解答」
Ⅰ.挑戦者が選んだ扉が当たりの事象と、 その余事象に場合分けするタイプの例
◇ 選んだ扉がハズレの確率が switch して賞品を獲得する確率と等しいことをやや丁寧に述べる解答
| switchしなければ、最初に選んだ扉が当たりのときしか勝てないが、switchすれば、最初に選ばなかった扉2枚のどちらかが当たりなら勝てるので、switchする方が2倍有利である。 |
Marilyn vos Savantの著書"The Power of Logical Thinking"(vos Savant, Marilyn (1996).)の中で同様な解答が紹介されている。
平成21年度中学3年学力テストでも、同様な解答を求めている。
「自動車」を「恩赦」、「ヤギ」を「処刑」と読み替えれば、3囚人問題に対しても同様な解答が可能である。
switch するかしないかの記述と、扉が当りかどうかの既述の順序を逆転させた表現もある。
| 選んだ扉がハズレなら、switch すると勝てるが、選んだ扉が当りなら switch すると負ける。 選んだ扉がハズレの確率は 2 / 3 だから、 switch すると勝てる確率は 2 / 3 である。 |
◇ switch するかしないかの意思決定をホストが扉を開ける前に行う場合に着目した解答
| ホストが扉を開く前に stay する決心をしたとすると、ホストがどの扉を残したかの影響を受けることができないので、ホストが扉を開ける前の時点の賞品を獲得する確率 1/3 から変わりがない。 |
「変わりがない」という言い回しから、「不特定事象による条件付確率あるいは事後確率の解答」のようであるが、stay の決心を扉が開けられる前に行っているので、「非条件付確率の解答」に含めるべきだろう。
この説明には、上記のAdams, Cecil (1990).が友人の助言のもとに考えた説明と似たところがある。
また、この説明とよく似た考え方が、DOFIさんが作った人気のページ「ネコでもわかるモンティホールジレンマ」の中の説明の一つで使われている。(2012年01月09日現在)
3囚人問題の場合には決心すなわち意思決定の要素がないため、このような解答は成立しない。
Ⅱ.3つの扉それぞれが当たりである場合に場合分けするタイプの例
◇ 扉と賞品の組合せ表による解答
挑戦者が扉1を選んだとする。
3つのケースのうち2ケースで switch すると自動車を得るので、switch して自動車を獲得する確率は 2/3となる。 |
"Ask Marilyn"での論争における、1990年12月のMarilyn vos Savant の解答は、ここに上げた表とほぼ同じものである。(vos Savant, Marilyn (1990b).)
「行動経済学 経済は「感情」で動いている」 (友野典男 著) 2006年5月初版 や、2003年出版のMark Haddon の小説。"the curious incident of the dog in the night-time"でも、説明に使われている。
NHK「ためしてガッテン」の平成23年の7月の放送でも、同様な図を使った説明がなされている状況を、インターネットの画像検索で見ることができる。(同番組のWebサイトからダウンロードできる放送内容のPDFファイルでは言葉だけで説明している)
この表は一見すると場合分けの表のように見えるが、下のように扉のパターンの部分を図に書き換えることができるので、 純然たる場合分けの表でないことがわかる。
挑戦者が扉1を選んだとする。
3つのケースのうち2ケースで switch すると自動車を得るので、switch して自動車を獲得する確率は 2 / 3 となる。 | |||||||||||||||||||||||||||||||||
1975年に Steve Selvin が統計学の雑誌に最初に発表した解答もこれに類似しているが、良く見ると樹形図のやり方に近いのでこれには含まれない。
Yahoo!知恵袋などのインターネットのQAサイトでは、マトリックスを次のように文字だけで表現する例もある。(初めて見たとき非常に感心しました)
|
〇×× | 〇× ×〇× | ×〇 ××〇 | ×〇 左はホストが扉を開く前、右は開いた後 |
数学の論文などでは、次のように文字配列のパターンを並べて書くだけの形式もある。
|
AGG, GAG, GGA A : Automobile (自動車) G : Goat (ヤギ) |
「自動車」を「恩赦」、「ヤギ」を「処刑」と読み替えれば、3囚人問題に対しても同様な解答が可能である。
Ⅲ.似たような別の問題になぞらえるタイプの例
「Ⅰ.挑戦者が選んだ扉が当たりの事象と、 その余事象に場合分けするタイプの例」の余事象の部分を具体的にイメージさせようとしている説明方法がある。
◇ 挑戦者が選んだ扉と残りの2つの扉との交換をホストが提案するゲームと等価だとする説明
例として、Adams, Cecil (1990).が友人の助言のもとに考えた説明をあげる。
Wkipedia(英語版)の"Monty Hall problem"の記事(2012年4月22日 2136の版)で 挑戦者が選ばなかった扉を一つに合体させる考え方の例としてこの説を引用している。
以下、この説明を 「開ける前に switch 説」 と呼ぶことにする。
「開ける前に switch 説」 を詳しく調べると本来のモンティ・ホール問題と異なる点がある。
扉の間の対称性に着目して 特定事象による条件付確率あるいは事後確率の問題設定 と 非条件付確率の問題設定 の関係を議論するができなくなっている。
「扉合体説」 のゲームでは挑戦者が当たりを選んだときに残りのはずれ扉のどちらを開けるかというホストのくせに影響されないからである。
|
次のように仮定してください。 あなたは扉1を選びます、 すると、あなたは扉1を開けるか、扉2と扉3の両方を開けるか、選択の機会が与えられます。 後者を選んだ場合、どちらかの扉に賞品があれば、それが手に入ります。 あなたは扉二つの方を選ぶでしょう? オリジナルの問題でも同等の機会が与えられています。 (オリジナルの問題では)あなたにモンティが、 「あなたの扉をキープしてもよいし、残りの二つに替えてもよい。 私は残りの二つの中からハズレの扉を一つ開けて上げよう。」と言ったのと同じだからです。 これでわかりましたか? |
以下、この説明を 「開ける前に switch 説」 と呼ぶことにする。
「開ける前に switch 説」 を詳しく調べると本来のモンティ・ホール問題と異なる点がある。
扉の間の対称性に着目して 特定事象による条件付確率あるいは事後確率の問題設定 と 非条件付確率の問題設定 の関係を議論するができなくなっている。
「扉合体説」 のゲームでは挑戦者が当たりを選んだときに残りのはずれ扉のどちらを開けるかというホストのくせに影響されないからである。
◇ 挑戦者が選ばなかった扉を合体させるゲームと等価だとする説明
例をあげる。
「開ける前に switch 説」 と本質的に同じものなので、本来のモンティ・ホール問題との相違点を同様に持っている。
扉の枚数を減らすアクションが含まれているので、本来のモンティ・ホール問題との類似度が 「開ける前に switch 説」 より高くなっている。
|
ホストがはずれの扉を一つ開けて、開いていない扉を一つ残すということは
挑戦者が選ばなかった扉を合体させて一つにすることと等価である。 合体させて一つになった扉は扉二つ分の当たりやすさを持っているから、 合体して一つになった扉に switch して当たる確率は 2/3 だ。 |
「開ける前に switch 説」 と本質的に同じものなので、本来のモンティ・ホール問題との相違点を同様に持っている。
扉の枚数を減らすアクションが含まれているので、本来のモンティ・ホール問題との類似度が 「開ける前に switch 説」 より高くなっている。
このようにさまざまな解答や説明が考案されているが、これらを読んだり理解したりしても、不思議さはなくならない。私自身の体験からそう思う。モンティ・ホール問題や3囚人問題の問題文を読むと無意識のヒューリスティクが本人の自覚抜きに標本空間を切り替えてしまうので、標本空間の切替をともなわないこれらの説明では、説明にならないからである。
ちまたで見かける「不特定事象による条件付確率あるいは事後確率の解答」
モンティ・ホール問題は事後確率の問題であるという立場に立ちながら、素朴な確率概念で理解できる解答をあれこれ工夫している人の中に、ホストが開ける扉をどれかの扉に特定化せずに、不特定な証拠事象の下で事後確率を説明しようとしている人を、インターネット上でたまに見かける。
そういう人たちは、事象の独立性の概念を無意識ながらにも使っているらしい。
こうした説明の例を一つ上げる。
そういう人たちは、事象の独立性の概念を無意識ながらにも使っているらしい。
こうした説明の例を一つ上げる。
◇ ホストが開ける扉がハズレに決まっていることを利用した解答
| ホストが開く扉がハズレであることは最初から分かっているので、ホストがハズレの扉を開いても、 最初に選んだ扉で賞品を獲得する確率 1/3 は変わらず、switch すると 1- 1/3 、すなわち 2/3 の確率で勝てる。 |
この解答は「必ず発生することが起きても確率に影響しない」というヒューリスティクに基づいているのだと思われる。
そうしたヒューリスティクは数学的に説明できるものなので、悪くない。まぎれもなく「不特定事象による条件付確率あるいは事後確率の解答」と見なすことができる。
※ 「必ず発生することが起きても確率に影響しない」ことは次のように確かめられる。
事象Bが起きても起きなくても事象Aが必ず発生するという条件で、事象Aを証拠事象とする事象Bの事後確率 P(B|A) を計算すると、
P(B|A) = P(A|B) × P(B) / P(A) = 1 × P(B) / 1 = P(B)
となって、事象Bの事前確率と一致する。
ただし、当たり扉の配置や恩赦の決め方が等確率でないことがわかっていたり、ホストがハズレ扉を開けるときや、看守が処刑される囚人の名を上げるときのくせがわかっていたりすると、特定事象による条件付確率あるいは事後確率の問題設定に比べて不特定事象による条件付確率あるいは事後確率の問題設定 が不利になることもあるので、注意が必要である。
Shimojo, S., & Ichikawa, S. (1989). に出て来る "irrelevant, therefore invariant" や Falk, R.(1992). に出てくる "no-news, no-change" を参考にして、 この論法を 「先刻承知確率不変説」 と私は呼ぶことにしている。
この解答の論法は3囚人問題でも使える。
ちまたで見かける「不特定事象による条件付確率あるいは事後確率の解答」を「特定事象による条件付確率あるいは事後確率の解答」に結びつけようとする解答
「不特定事象による条件付確率あるいは事後確率の解答」を求めてから、「特定事象による条件付確率あるいは事後確率の解答」を導こうとする人がいる。大概は後段で扉の対象性を使っていないので、後述の「確率継承説」の匂いが消えないものが多い。
◇ ホストが開ける扉がハズレに決まっていることを利用しつつ、ホストが開けた扉を特定してしまった解答
|
ホストが開く扉がハズレであることは最初から分かっているので、 ホストがハズレの扉3 を開いても、最初に選んだ扉1 で賞品を獲得する確率 1 / 3 は変わらず、 switch すると 1 - 1 / 3 、すなわち 2 / 3 の確率で勝てる。 |
上で取り上げた 「ホストが開ける扉がハズレに決まっていることを利用した解答」 によく似ているが、残念ながら、ホストが開けた扉を特定してしまっている。
扉2 と扉3 の間の対称性に触れるか、もしくは「特定事象による条件付確率あるいは事後確率の解答」 に帰着させないことを宣言するかしなければ、 この説明は 「数学的に不完全」、 もしくは「数学的に誤り」 と言わざるを得ない。
この説明の勘違いを 「先刻承知確率不変説の過剰適用」 と私は呼ぶことにしている。
|
(あなたが扉Aを選び、ホストが扉Cを開けたとして) 扉を開けることによって、モンティは挑戦者に次のように述べたことになる。 「・・・途中省略・・・ あなたが扉Aで勝つチャンスは 1/3 である。 私はそれを変化させなかった。 しかし扉Cを除くことによって、扉Bが賞品を隠している確率が 2/3 であることをあなたに示した。」 |
前段の「私はそれを変化させなかった。」のくだりは数学的にかなり端折った表現になっているが、Devlin はちゃんと事象の独立性を考慮しているのだろう。しかし後段の「扉Bが賞品を隠している確率は 2/3 に変わった。」の部分は途中の論理が大きく省略されているので、きちんと扉の間の対象性を考慮せずに 「先刻承知確率不変説の過剰適用」 となっている。
あるいはもしかしたら後述の「確率継承説」に基づいた論理なのかもしれない。
Wkipedia(英語版)の"Monty Hall problem"の記事(2012年4月22日 2136の版)で、挑戦者が選ばなかった扉を一つに合体させる考え方の例としてこの説を引用しているのは、私にはこじつけに感じられる。
ちまたで見かける「確率継承説」による説明
モンティ・ホール問題は事後確率の問題であるという立場に立ちながら、素朴な確率概念で理解できる解答をあれこれ工夫している人の中に、「確率継承説」とでも言うべき迷信的な考え方に迷いこんだ人をよく見かける。 私もその一人で、挑戦者が選んだ扉が当たりである確率がホストが扉を開ける前後で変わらずに、ホストが開け残した扉に残りの確率が集中することを説明しようとして「確率継承説」に迷いこみ、しばらく抜け出すことができなかった。
◇ 例1
|
(挑戦者が扉Aを選び、ホストが扉Cを開けたとして) 扉Aが正しい選択であるチャンスは 1/3 で、扉Bまたは扉Cで勝つオッヅは 2/3 である。 扉Cが除かれたことによって、扉Bが確率 2/3 を継承する。 |
この考え方は、2001年1月に出版された "Butterfly Economics: A New General Theory of Social and Economic Behavior"の中で使われている。この本のある書評によると、オームロッドは上のように説明しているらしい。この説明は、上記のDevlin, Keith (July ‐ August 2003). の説明に似ているが、「確率継承説」の匂いが「継承する」という言葉で強められている。
◇ 例2
Devlin, Keith (July ‐ August 2003). が試みたさまざまな説明の1つ
この説明の中の 「移りました ( shifted ) 」 という言葉から、「確率継承説」の匂いが強く感じられる。
|
モンティが3つのうちの1つの扉を開けて賞品がないことを示してから switch の機会をあなたに与えたとき、結果として彼はあなたに1つから2つへの switch を提案したに等しくなります。
あなたは最初に扉Aを選びました。彼は今 「扉Aと扉Bと扉Cの2つとを交換しませんか? そうだ、あなたが交換するか決める前に、あなたのため、その2つの扉の1つ(賞品がないもの)を開けましょう。」 と言っています。モンティが扉Cを開けると、結果として扉Bまたは扉Cの後ろに賞品がある魅力的な確率 2/3 が扉Bだけに移りました。 |
この説明の中の 「移りました ( shifted ) 」 という言葉から、「確率継承説」の匂いが強く感じられる。
◇ 例3
|
(ホストが扉3を開けた後の図に対して) 通常の仮定の下では、プレイヤーの選択の勝機は 1/3 のままで、残り二つを合体させたものの勝機は 2/3 のままであり、開け残されたものに 2/3 が残り、0 が開けられたものに残る。 |
この図と文は Wkipedia(英語版)の"Monty Hall problem"の記事で、挑戦者が選ばなかった二つの扉を合体させて考える方法の段落で使われている。(図は私が模写したもので原図ではない)
この文の中の「残る」という表現から「確率継承説」の匂いが強く感じられるが、本文で引用しているAdams, Cecil (1990).の説明やDevlin, Keith (July ‐ August 2003). の説明 (上の例で上げた説明とは別もの) の方にはあまり感じられない。
Wikipedia(英語版)の図と同じものが、Wikipedia(日本語版)の「モンティ・ホール問題」の記事でも使われていて、2012年4月22日 (日) 19:42の版の説明文では英語版の「残る」という表現の代わりに、「集中する」と言う表現になっている。
◇ 例4
| 田中が選んだ紙コップにキャンディがある確率は1/4で、田中が選ばなかった3個の紙コップの中にキャンディーがある確率は 3/4。 2個の紙コップがハズレだとわかっても田中が選ばなかった紙コップの中に当たりがある確率は変わらないので、残った紙コップに、確率3/4が残る。 |
2011年7月8日のNHK 「23:55」 の中で、爆笑問題の田中に太田が出題するという形式でモンティ・ホール問題が披露されたときの説明を、テレビ放送を観てあまり記憶が薄れないうちに書き留めたものである。
田中が選ばなかった紙コップが一つのグループを形成していることを、イラストのように画像合成で示していた。
「確率継承説」の匂いが「確率3/4が残る」という表現から感じられる。
これらの説明はいずれも次のような構造になっている。
- ①3つの扉を挑戦者が選んだ扉のブループA とそれ以外のグループB に分けて、それを意識させることで、それぞれのグループの中に当りがある確率が変わらないことを理解させようとしている。
- ②最終的にグループB の中の特定もしくは不特定の開け残された扉にグループB の確率が集中するとしている。
しかし、
①のステップについていうと、二つのグループに分けることには数学的にはあまり意味がない。数学的に説明するためには、事象の独立性の説明を省略することができないからである。
②のステップについていうと、グループB のこれこれの扉に確率が集中すると説明したいのであれば、グループB に属する扉の間の対象性を明確に述べなければ、数学的には減点である。
結局これらの説明は、次のような素朴な確率論に合うようにひねり出した苦肉の策なのだろう。
- ①確率を相対的な「率」でなく絶対的な「量」のようにとらえている。
- ②確率という「量」に保存則が成立すると考えている。
つまり、これらの解答は「確率継承説」」と呼べるような一種の迷信に基づいていると言える。
じつは私もこうした迷信にはまっていた一人で、しかもかなり長い間はまっていた。
「確率継承説」が間違いであることを一発で論証
特定事象による条件付確率あるいは事後確率の解答を得たつもりの説明に対して
扉2と扉3の中に当りがある確率 2/3 が残った特定の扉2に継承されるという説明の誤りは、扉の間の対象性を無くして考えればよい。例えば、扉1、扉2、扉3 のそれぞれが当りである事前確率がそれぞれ、0.2、0.5、0.3 で、挑戦者が扉1を選んで、ホストが扉3を開けた場合、「確率継承説」では扉2が当りである事後確率が 0.8 ( = 0.5 + 0.3 ) となるが、実際の事後確率 0.833・・・ ( = 0.5 / ( ( 0.2 ÷ 2 ) + 0.5 ) となって、一致しないことから、「確率継承説」が誤りであることがわかる。
不特定事象による条件付確率あるいは事後確率の解答を得たつもりの説明に対して
「確率継承説」による説明をする人が、特定事象による条件付確率あるいは事後確率の解答を得たつもりでなく、不特定事象による条件付確率あるいは事後確率の解答を得たつもりなのかも知れない。そうした場合には、事象の独立性がないケースを考えればよい。
「確率継承説」では、挑戦者が選ばなかった扉の中から、ホストが あてずっぽう に扉を開けたケースも含んでいる。NHKの 「23:55」 で言えば、太田が田中に あてずっぽう で開けるコップを指示した場合も含んでいる。
このような場合に残った扉やコップが当りである事後確率 は 1/2 になって、「確率継承説」の予想と反してしまうことから、「確率継承説」が誤りであることがわかる。
「確率継承説」では、挑戦者が選ばなかった扉の中から、ホストが あてずっぽう に扉を開けたケースも含んでいる。NHKの 「23:55」 で言えば、太田が田中に あてずっぽう で開けるコップを指示した場合も含んでいる。
このような場合に残った扉やコップが当りである事後確率 は 1/2 になって、「確率継承説」の予想と反してしまうことから、「確率継承説」が誤りであることがわかる。
【ちょっと寄り道】 NHKの深夜番組「23:55」でのモンティ・ホール問題
上で示したように、2011年7月8日23:55に放送された「23:55」の爆笑問題のコーナーでモンティ・ホール問題が取り上げられたが、そのときの太田のとぼけた声と、田中のとぼけた表情が面白かった。
田中の前に紙コップ4個が伏せられている。
太田:「ひとつの紙コップにキャンディがある」
太田:「田中が選んだ紙コップにキャンディがあればそれを食べられる。」と述べて田中に選ばせる。
田中:画面向かって左端の紙コップを選ぶ。
太田:「田中にいいことを教えて上げよう。画面向かって右端の紙コップは空だ。開けて見なさい」
田中:右端の紙コップを開けて、中をカメラに向ける。
太田:「もう一ついいことを教えて上げよう。一つ置いた紙コップも空だ。開けてみなさい」
田中:右から3番目の紙コップを開けて、中をカメラに向ける。
太田:「2個の紙コップが残った。紙コップを変えてもよいがどうする?」
田中:最初に選んだ紙コップを開けて空であることを示す。がっかりはしていない。
太田の「田中にいいことを教えて上げよう」という言葉から、「天使モンティ」である可能性が高くなってしまっている。種明かしの後で、田中はキャンディを食べさせてもらっている。 なにやら物思いにふけっているような表情で、太田の説明をいぶかしんでいるようにも見えた。
Bertrand's box paradox
三つの箱の一つに2枚の金貨、もう一つに2枚の銀貨、残りの一つに金貨か銀貨のどちらか1枚が入っている。ランダムに箱を選んで、中からランダムに硬貨を取り出したら金貨であった。残りの1枚が金貨である確率は?
Three-Card Swindle
一枚のカードの両面に赤い印、もう一枚のカードの片面に赤、反対の面に黒い印、残りのカードの一面に赤か黒の印を付ける。ディーラーがランダムに帽子から取り出して片面を見たら赤い印が付いていた。反対の面も赤の印が付いているかどうか、ディーラーと客の間で掛けを行う。
Boy or Girl paradox (The Two Children Problem)
- 〇Mr.Jones has two children. The older child is a girl. What is the probability that both childeren are girls?
- 〇Mr.Smith ha s two childeren. At least one of them is a boy. What is the probability that both children are boys?
最初に抜いたカードがスペードである確率
よく切った一組のトランプを裏返しにして、その中から1枚抜いて裏返しのまま置く。残りからランダムにカードを n 枚抜いたらすべてスペードだった。最初に抜いたカードがスペードである確率は?
モンティ・ホール問題の歴史
モンティ・ホール問題が文献に現れるのは、TVゲームショー"Let's Make A Deal"の中のゲームの一つを見た Steve Selvin が そのゲームの確率に関するパズル風の小論を 1975年に American Statiscian の1975年2月号の"Letters to the Editor"のコーナーに発表したことが最初である。(Selvin, Steve (1975a).)
Steve Selvin は、モンティ・ホールが行っているゲームに関する確率について標準仮定を仮定しつつ「非条件付確率の問題設定(挑戦者が選ぶ扉を限定しない方法)」で答えを出している。
統計数学の学会誌に提出していることや、Monty Hall 本人に書簡を送って意見を求めていることを考え合わせると、Steve Sevin は現実の実際のゲームの確率を論じているつもりだったのかも知れない。
2月号に発表した内容への反論に答えて、同じ年の8月号に「特定事象による条件付確率あるいは事後確率の解答」を Steve Selvin が発表している。(Selvin, Steve (1975b).)
8月号に発表した小論には Monty Hall からの返事が引用されていて、それによると Monty Hall は、Steve Selvin が想定したような標準仮定が実際のゲームでは成立しないことを述べている。
このことから、モンティ・ホール問題のゲームと Monty Hall の実際のゲームとの関連性は、当初から薄かったことがわかる。
現在、モンティ・ホール問題の問題文の基準とされている"Ask Marilyn"の問題文に酷似している Barry Nalebuff の問題文が現れたのは、1987年のことであった。(Nalebuff, Barry (1987).)
モンティ・ホール 問題が有名になるきっかけは、米国の日曜ニュース雑誌 PARADE のコラム "Ask Marilyn"での1990年から1991年に掛けての大論争である。(vos Savant, Marilyn (1990).;vos Savant, Marilyn (1990b).;vos Savant, Marilyn (1991).)
"Ask Marilyn"は読者が出した問題に自称女性最高IQ保持者のMarilyn vos Savant が答えるというものである。Craig F.Whitaker が投稿したモンティ・ホール問題に対して switch が有利だと Marilyn vos Savant が回答したところ、大勢の読者から反論が殺到するという大騒ぎになった。
このときの問題文には Let's Make A Deal や Monty Hall などの固有名詞が書かれておらず、現実のゲーム番組から離れた純粋な数学パズルであった。
1991年7月21日(日)のNew York Times の日曜版の記事 "Behind Monty Hall's Doors - Puzzle, Debate and Answer? -" (Tierney, John (1991).)で大々的に取り上げられたことが、モンティ・ホール問題を世界に広めるきっかけだったに違いない。
この記事の中で "Ask Marilyn"で大論争になった問題が "Monty Hall Problem" 、" Monty Hall Dilemma" 、"Monty Hall Paradox" などの呼び名で知られていた問題だったことも報告されている。この記事が無かったら、モンティ・ホール問題を、「3扉問題」とか、「自動車とヤギ」などと呼ぶようになっていたかも知れない。現に、Wikipedia(ドイツ語版)では今でも「ヤギ問題」と呼んでいる。(2011年5月現在)
問題文に回答したMarilyn vos Savant も、さらに彼女の回答に反論した読者たちのほとんども標準仮定のもとに議論していた。
このころのエピソードとして、放浪の天才数学者として知られていたエルデーシュのケースがある。
エルデーシュの10代からの数学友達のヴァージョニの書いた Vazsonyi, Andrew (1999). を読むと次のことがわかる。
Steve Selvin は、モンティ・ホールが行っているゲームに関する確率について標準仮定を仮定しつつ「非条件付確率の問題設定(挑戦者が選ぶ扉を限定しない方法)」で答えを出している。
統計数学の学会誌に提出していることや、Monty Hall 本人に書簡を送って意見を求めていることを考え合わせると、Steve Sevin は現実の実際のゲームの確率を論じているつもりだったのかも知れない。
2月号に発表した内容への反論に答えて、同じ年の8月号に「特定事象による条件付確率あるいは事後確率の解答」を Steve Selvin が発表している。(Selvin, Steve (1975b).)
8月号に発表した小論には Monty Hall からの返事が引用されていて、それによると Monty Hall は、Steve Selvin が想定したような標準仮定が実際のゲームでは成立しないことを述べている。
このことから、モンティ・ホール問題のゲームと Monty Hall の実際のゲームとの関連性は、当初から薄かったことがわかる。
現在、モンティ・ホール問題の問題文の基準とされている"Ask Marilyn"の問題文に酷似している Barry Nalebuff の問題文が現れたのは、1987年のことであった。(Nalebuff, Barry (1987).)
モンティ・ホール 問題が有名になるきっかけは、米国の日曜ニュース雑誌 PARADE のコラム "Ask Marilyn"での1990年から1991年に掛けての大論争である。(vos Savant, Marilyn (1990).;vos Savant, Marilyn (1990b).;vos Savant, Marilyn (1991).)
"Ask Marilyn"は読者が出した問題に自称女性最高IQ保持者のMarilyn vos Savant が答えるというものである。Craig F.Whitaker が投稿したモンティ・ホール問題に対して switch が有利だと Marilyn vos Savant が回答したところ、大勢の読者から反論が殺到するという大騒ぎになった。
このときの問題文には Let's Make A Deal や Monty Hall などの固有名詞が書かれておらず、現実のゲーム番組から離れた純粋な数学パズルであった。
1991年7月21日(日)のNew York Times の日曜版の記事 "Behind Monty Hall's Doors - Puzzle, Debate and Answer? -" (Tierney, John (1991).)で大々的に取り上げられたことが、モンティ・ホール問題を世界に広めるきっかけだったに違いない。
この記事の中で "Ask Marilyn"で大論争になった問題が "Monty Hall Problem" 、" Monty Hall Dilemma" 、"Monty Hall Paradox" などの呼び名で知られていた問題だったことも報告されている。この記事が無かったら、モンティ・ホール問題を、「3扉問題」とか、「自動車とヤギ」などと呼ぶようになっていたかも知れない。現に、Wikipedia(ドイツ語版)では今でも「ヤギ問題」と呼んでいる。(2011年5月現在)
問題文に回答したMarilyn vos Savant も、さらに彼女の回答に反論した読者たちのほとんども標準仮定のもとに議論していた。
このころのエピソードとして、放浪の天才数学者として知られていたエルデーシュのケースがある。
エルデーシュの10代からの数学友達のヴァージョニの書いた Vazsonyi, Andrew (1999). を読むと次のことがわかる。
- ヴァージョニは友人から聞いたモンティ・ホール問題を決定木(※参照)を使って解いた。 (その決定木は、「非条件付確率の問題設定」 によるものだった)
- 1995年 (エルデーシュ 82歳前後) にヴァージョニがエルデーシュに説明したが、エルデーシュは決定木(※参照)による説明を理解しなかった。
- ヴァージョニがパソコンを使ってモンテカルロ法でシミュレーションして見せるとエルデーシュはヴァージョニが正しいが、その理由が理解できないと述べた。 (エルデーシュはモンテカルロ法の知識があったというよりも、モンテカルロ法の開発者と知己であった)
- 数日後、友人のグラハムの説明で理解したとエルデーシュからヴァージョニに電話があった。
このときのグラハムの説明内容が、ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月) の最後の方に書かれているので、抜粋すると次のようになる。
「司会者がかならず別のドアに変えるチャンスをくれるということをあらかじめ知っていることが鍵になるんだ。
それが問題を解くときに考慮に入れておかなければならないゲームのルールのひとつだ」
---ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月)
それが問題を解くときに考慮に入れておかなければならないゲームのルールのひとつだ」
---ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月)
- ※ポール・エルデーシュはハンガリーの数学者。(1913~1996 ハンガリー語でエルデーシュ・パール)
Wikipedia(日本語版)によると、数論、組合せ論、グラフ理論、集合論、確率論、級数論など 幅広い分野で膨大な結果を残し、 特にセルバーグと共に素数定理の初等的な証明を発見したことが有名 - ※他の文献でヴァージョニが使ったとされる決定木を見たところ、「確率樹形図」に似ていなくもない。
"Ask Marilyn"での論争後数年経ってからは、事後確率の問題に直面した場合に無意識に行う素朴な確率判断の心理学的研究材料として、盛んに取り上げらるようになった。
モンティ・ホール問題が有名になるにつれて、TVドラマ、小説、映画、行動経済学の本、平成教育委員会などにも登場するようになった。
2009年には日本の中学3年の学力テストの問題になるに至った。
Wikipedia に載るようになったのは2001年のことであったが当初は英語版の Wikipedia ですら自己流の問題文を採用していた。
しかし、2011年9月現在では、大概の言語の Wikipedia で"Ask Marilyn"の問題文を採用するようになっている。
モンティ・ホール 問題の問題文のいろいろ
問題文に様々なバリエーションがあることが、モンティ・ホール問題の特徴である。以下、歴史的に重要だったり、賞品の隠し場所が変化したり、賞品が面白かったりしていて興味を引くものを年代順に上げる。
Selvin, Steve (1975a).の問題文
モンティ・ホール問題の問題文として文献に表れた最も古いものである。ある日のテレビ番組の録音筆記のような文体である。問題文を作った Steve Selvin は、現実のゲームに確率論を応用しているつもりだったのかも知れない。
問題文の特徴
この問題文の中の"I'll do you a favor and open one of the remaining boxes on the table (he opens box A)."という文により、標準仮定のうちの「②ホストは挑戦者の選んだ扉を開けない」と「④ホストはハズレの扉しか開けない」が明確になっている。
問題文の特徴
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 化けていない | 勘違いしていない | 手で掴むことの出来るサイズの箱 |
当りの箱に自動車のキー ハズレの箱は空 |
いる | いない |
(選らんだ箱を掴んでいる挑戦者に対して) "I'll do you a favor and open one of the remaining boxes on the table (he opens box A)." --- Selvin, Steve (1975a).から |
"Ask Marilyn"並 | いる | いる |
この問題文の中の"I'll do you a favor and open one of the remaining boxes on the table (he opens box A)."という文により、標準仮定のうちの「②ホストは挑戦者の選んだ扉を開けない」と「④ホストはハズレの扉しか開けない」が明確になっている。
胡桃の殻とエンドウ豆の問題(1982)
"Impossible?:suprising solutions to counerintuitive coundrums" (著者 Julian Havil )によると、
Aha! Gotcha book (Gardner, Martin (1982). )の中に胡桃の殻とエンドウ豆を使ったバクチに関するパズルがあって、次のような内容であるらしい。
Aha! Gotcha book (Gardner, Martin (1982). )の中に胡桃の殻とエンドウ豆を使ったバクチに関するパズルがあって、次のような内容であるらしい。
3個の胡桃の殻のどれにエンドウ豆があるか当てたら掛け金が2倍になるというゲームをやっていた
勝つ確率が 1/3 しかないことに気付いたマークさんが立ち去ろうとしたらオペレータが次のように提案した。
今度からは、マークさんが選ばなかった殻のうちハズレの一つをひっくり返しましょう。そうすればエンドウ豆がある殻が2つに減るからマークさんが勝つ確率が上がります。
哀れなマークさんは、あっという間にスッテしまいました。
ゲーム内容がモンティ・ホール問題にそっくりであるので、モンティ・ホール問題の一種だと考えてよいだろう。
エンドウ豆を仕込む人物と殻を開ける人物が同一人物( オペレータ) であったり、必ず別の殻を開けるとオペレータ が宣言し、かつ何度も実行したりしている点が、通常のモンティ・ホール問題や3囚人問題と大きく異なっている。
Steve Selvin の問題文と並んで、モンティ・ホールのゲーム番組を実際に見た人間が作ったことがはっきりしている問題文の一つである。今日、モンティ・ホール問題の問題文の基準とされている"Ask Marilyn"の問題文と、固有名詞の有無を除いてそっくりである。ホストが現金など第4の選択肢との交換の提案をしていない点も、モンティ・ホールの実際のゲームから離れた純粋数学パズルらしさである。
問題文の特徴
問題文の特徴
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 化けていない | 勘違いしている可能性が高い | カーテン |
当りのカーテンにグランド賞 その他のカーテンに、ささやかな賞品 |
いる | いる |
仮装した挑戦者が選ぶと、モンティ・ホールは選ばれなかった二つのカーテンの一つの後ろに何があるか見せる。 今までの番組の歴史を通して、選ばれなかったカーテンを開けてグランド賞を見せたことがないことから、三つのカーテンそれぞれの後ろに何があるかをモンティが知っているに違いない。 ---Nalebuff, Barry (1987).の一部翻訳 |
"Ask Marilyn"並 | いない | いない |
"Ask Mariln" の問題文(1990年にPARADE誌に掲載、投稿はその1~2年前)
Craig F.Whitaker という数学の先生が "Ask Mariln"に出題した問題文である。
(内容については、「第一部 モンティ・ホール問題と3囚人問題の問題文と解法」 を参照)
モンティ・ホール問題の問題文の中で最も有名であり、標準仮定をくどくどと既述するような野暮な問題文でもなく、誤解を誘うほど雑な問題文でもないので、モンティ・ホール問題の問題文の基準と考えてよかろう。なお、大概の人がこの問題文から標準仮定を読み取ることがわかっている。
問題文の特徴
2003年出版のMark Haddon の小説"the curious incident of the dog in the night-time"で"Aks Marilyn"の問題を題材にしていて、Craig F. Whitaker さんの名も出てくることから、その少し後に彼に対して新聞 (たぶん New York Times) の取材が行われている。その記事によると、彼が友人から聞いた問題を"Ask Marilyn"に投稿したのは、雑誌に掲載される約2年前のことらしいので、投稿したのは 1988~1989年ごろとなる。
同じ記事によると、モンティ・ホール問題が "Ask Marilyn" に掲載された 1990年9月9日(日曜) の朝6時に "Ask Marilyn"の読者から抗議の電話が彼の元に掛かって来て、その日の後も、 数件掛かって来たらしい。
Let's Make A Dealの公式サイトの既述によると、1987~1989年ごろは Let's Make A Deal のTV放送休止期間であったことがわかる。
インターネットで見たMonty Hall へのインタビュー記事によると、同じ時期に、ディズニー・ワールドのアトラクションとして興行されていたこともあるらしい。
この問題文は Nalebuff の問題文によく似ているので、Craig F. Whitaker さん自身、もしくは彼の友人が Nalebuff の問題文を読んだのだろう。
しかし、この問題文は次の点で Nalebuff の問題文と大きく異なっている。
ホストが賞品のありかを知っているケースと知らないケースの両方を Marilyn vos Savant が取り上げていたら、 「後者のケースでは switch してもしなくても当る確率は同じ」 と答えていただろう。 そして無意識の確率判断が出す直感的な答えと一致して人々を安心させるから、 大勢の人が反論する騒動にならなかっただろう。 ホストが賞品のありかを知っているケースと知らないケースを比較できるような分析をしなければならないから、大勢の博士たちがうっかり反論するようなことも無かったろう。 そして New York Times で取り上げられることもなく、モンティ・ホール問題が世界的に有名になることもなかっただろう。
問題文に "Monty Hall" という固有名詞が書かれていないのは、 Craig F. Whitaker さんが友人から問題文を教わったとき Monty Hall が有名人であることを知らなかったため記憶に残らなかったのかも知れないし、 その他にも色々な理由が考えられるが、 上記のようなことがあるので Marilyn vos Savant によって伏せられた可能性もなきにしもあらずである。
(内容については、「第一部 モンティ・ホール問題と3囚人問題の問題文と解法」 を参照)
モンティ・ホール問題の問題文の中で最も有名であり、標準仮定をくどくどと既述するような野暮な問題文でもなく、誤解を誘うほど雑な問題文でもないので、モンティ・ホール問題の問題文の基準と考えてよかろう。なお、大概の人がこの問題文から標準仮定を読み取ることがわかっている。
問題文の特徴
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 化けていない | 言及なし | 扉 |
当りの扉に自動車 その他の扉にヤギ |
いない | いる |
あなたは一つの扉、たとえば扉1を選び、どの扉の後ろに何があるか知っているホストが、ヤギがいると知っている別の扉、たとえば扉3を開けます。 ---Whitaker, Craig F. (1990). の一部翻訳 |
"Ask Marilyn"の問題文そのもの | いない | いる |
2003年出版のMark Haddon の小説"the curious incident of the dog in the night-time"で"Aks Marilyn"の問題を題材にしていて、Craig F. Whitaker さんの名も出てくることから、その少し後に彼に対して新聞 (たぶん New York Times) の取材が行われている。その記事によると、彼が友人から聞いた問題を"Ask Marilyn"に投稿したのは、雑誌に掲載される約2年前のことらしいので、投稿したのは 1988~1989年ごろとなる。
同じ記事によると、モンティ・ホール問題が "Ask Marilyn" に掲載された 1990年9月9日(日曜) の朝6時に "Ask Marilyn"の読者から抗議の電話が彼の元に掛かって来て、その日の後も、 数件掛かって来たらしい。
Let's Make A Dealの公式サイトの既述によると、1987~1989年ごろは Let's Make A Deal のTV放送休止期間であったことがわかる。
インターネットで見たMonty Hall へのインタビュー記事によると、同じ時期に、ディズニー・ワールドのアトラクションとして興行されていたこともあるらしい。
この問題文は Nalebuff の問題文によく似ているので、Craig F. Whitaker さん自身、もしくは彼の友人が Nalebuff の問題文を読んだのだろう。
しかし、この問題文は次の点で Nalebuff の問題文と大きく異なっている。
- Nalebuff の問題文
- ゲームのルールを説明してから、自分が挑戦者だったらどうするかを聞いている
- Whitaker の問題文
- ゲームのルールを説明する前に、自分が挑戦者であると想像させている
ホストが賞品のありかを知っているケースと知らないケースの両方を Marilyn vos Savant が取り上げていたら、 「後者のケースでは switch してもしなくても当る確率は同じ」 と答えていただろう。 そして無意識の確率判断が出す直感的な答えと一致して人々を安心させるから、 大勢の人が反論する騒動にならなかっただろう。 ホストが賞品のありかを知っているケースと知らないケースを比較できるような分析をしなければならないから、大勢の博士たちがうっかり反論するようなことも無かったろう。 そして New York Times で取り上げられることもなく、モンティ・ホール問題が世界的に有名になることもなかっただろう。
問題文に "Monty Hall" という固有名詞が書かれていないのは、 Craig F. Whitaker さんが友人から問題文を教わったとき Monty Hall が有名人であることを知らなかったため記憶に残らなかったのかも知れないし、 その他にも色々な理由が考えられるが、 上記のようなことがあるので Marilyn vos Savant によって伏せられた可能性もなきにしもあらずである。
Paul Ormerod が書いた経済学書に載った曖昧なモンティ・ホール問題(2001)
2001年1月に出版された "Butterfly Economics: A New General Theory of Social and Economic Behavior", Paul Ormerod 著の中の例である。彼は、"very simple problem . . . yet people usually get it wrong."の例としてモンティ・ホール問題を取り上げている。
あるブログに、邦訳「バタフライ・エコノミクス」の中の問題のくだりが引用されていて、それによると次のような問題文らしい。
問題文の特徴
ホストの行動ルールに関する記述がこんな具合では、標準仮定を読み取らない人が多そうであるが、上記のブログのオーナーが標準仮定に基づいたシミュレーションプログラムを書いていることから、これぐらいの曖昧さでもまだ標準仮定を読み取れることがわかる。
あるブログに、邦訳「バタフライ・エコノミクス」の中の問題のくだりが引用されていて、それによると次のような問題文らしい。
問題文の特徴
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 化けていない | 勘違いしている | 扉 |
当りの扉に一万ドル その他の扉にアヒルのおもちゃ |
いる | いない | 司会者のモンティは、Cのドアを開けて (モンティはどのドアに何が隠されているのかを、すべて承知している) アヒルのおもちゃが置かれているのを見せて、さらに緊張を高める。 | "Ask Marilyn"より劣る | いない | いる |
ホストの行動ルールに関する記述がこんな具合では、標準仮定を読み取らない人が多そうであるが、上記のブログのオーナーが標準仮定に基づいたシミュレーションプログラムを書いていることから、これぐらいの曖昧さでもまだ標準仮定を読み取れることがわかる。
「行動経済学 経済は「感情」で動いている」(友野典男 著) の問題文 (2006年5月初版)
私がモンティ・ホール問題にはまる切っ掛けになった問題文である。扉、自動車、ヤギという道具立ては、"Ask Marilyn"の問題文の流れをくんでいるが、ゲーム番組がクイズ番組に化けたり、番組最後のゲームをモンティ・ホール問題のゲームのモデルだと勘違いしたりしているので、色々な人を経由して出来上がった問題文のようである。
問題文の特徴
この問題文は過去形で書かれているため、標準仮定の曖昧さが"Ask Marilyn"の問題文より増している。
問題文の特徴
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 化けている | 勘違いしている | 扉 |
当りの扉に自動車 その他の扉にヤギ |
いない | いる | すると、どのドアの後ろに車があるのか知っている司会者は、Cのドアを開けた。もちろん、そこにはヤギがいるだけだ。 | "Ask Marilyn"よりやや劣る | いない | いる |
この問題文は過去形で書かれているため、標準仮定の曖昧さが"Ask Marilyn"の問題文より増している。
Wikipedia(英語版)の"Monty Hall Problem"の記事の問題文
21:29, 22 September 2001の初版の問題文
初版では"Ask Marilyn"の問題文ではなく、下記のような自己流の問題文を採用している。
確率数値を求めておらず、挑戦者が選んだ扉やホストが選んだ扉を特定するような表現もしていない点は、前述したNalebuff, Barry (1987).の問題文によく似ている。
問題文の特徴
この初版が書かれた時期は"Ask Marilyn"の問題文を基準にすることが一般化していなかったので、Wikipediaの英語版でありながら"Ask Marilyn"の問題文を使っていなくても奇異ではない。The problem is as follows: at the end of the show, a player is shown three doors. Behind one of them, there's a car for him to keep, behind the other two there are goats. Of course, the player does not know where the car is, but Monty knows. The player chooses one door. Before that door is opened however, Monty opens one of the two other doors with a goat behind it. He then allows the player to switch to the other closed door. Should the player switch?
確率数値を求めておらず、挑戦者が選んだ扉やホストが選んだ扉を特定するような表現もしていない点は、前述したNalebuff, Barry (1987).の問題文によく似ている。
問題文の特徴
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 番組の種類不明 | 勘違いしている | 扉 |
当りの扉に自動車 その他の扉にヤギ |
いる | いない | Of course, the player does not know where the car is, but Monty knows.The player chooses one door. Before that door is opened however, Monty opens one of the two other doors with a goat behind it. | "Ask Marilyn"並 | いない | いない |
23:56, 19 June 2003 の版の問題文
ホストが扉を開けるときのルールが初版よりも曖昧になっている。日本語版の初版の原文でもある。
問題文の特徴At the end of the show, a player is shown three doors. Behind one of them, there's a prize for him to keep, while the other two contain goats (signifying no prize to be won). Although the show host knows what is behind each door, of course the player does not. After the player makes a first choice, Monty opens one of the two other doors, revealing a goat. ※ ヤギのいる扉を選んで開けているのか、開けたところにたまたまヤギがいたのか、曖昧である。 He then offers the player the option to either stick with the initial choice or switch to the other closed door. Should the player switch?
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 番組の種類不明 | 勘違いしている | 扉 |
当りの扉に賞品 その他の扉にハズレを意味するヤギ |
いる | いない | Although the show host knows what is behind each door, of course the player does not. After the player makes a first choice, Monty opens one of the two other doors, revealing a goat. | "Ask Marilyn"より劣る | いない | いない |
22:48, 12 March 2004の版の問題文。
"Ask Marilyn"の問題文を世界のWikipediaで初めて採用した。
Wikipedia(日本語版)の「モンティ・ホール問題」の記事の問題文
2003年7月11日 (金) 17:56 の初版の問題文
Wikipedia(英語版) の 23:56, 19 June 2003 の版の標準仮定が曖昧な問題文を訳したものである。
問題文の特徴ショーの終わりに、プレイヤーは三つのドアを見せられる。 ドアの一つの後ろにはプレイヤーが得ることができる景品があり、 一方、他の二つのドアには羊(景品がなく、ハズレであることを意味している)が入っている。 しかし、ショーのホストはそれぞれのドアの後ろに何があるか知っており、もちろんプレイヤーは知らない。 プレイヤーが第一の選択をした後、モンティ(ホスト)は他の二つのドアのうち一つをあけ、羊をみせる。 そしてホストはプレイヤーに、初めの選択に忠実であるか、もう一つの閉じているドアに変更するか、どちらかの選択権を提供する。 プレイヤーは、選択を変更すべきだろうか?
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 番組の種類不明 | 勘違いしている | 扉 |
当りの扉に景品 その他の扉にハズレを意味する羊 |
いる | いない | しかし、ショーのホストはそれぞれのドアの後ろに何があるか知っており、もちろんプレイヤーは知らない。プレイヤーが第一の選択をした後、モンティ(ホスト)は他の二つのドアのうち一つをあけ、羊をみせる。 | "Ask Marilyn"より劣る | いない | いない |
2010年2月8日 (月) 11:20 の版の問題文
ホストが扉を開けるルールの曖昧さが初版よりかなり薄れてはいるものの、相変わらず初版の問題文をベースにしている。
他の言語のWikipediaがこぞって"Ask Marilyn"の問題文を採用している中で、日本語版のように独自の問題文を採用しているWikipediaは国際的に少数派である。(2011年4月28日 現在)
問題文の特徴プレイヤーの前に3つのドアがあって、1つのドアの後ろには賞品の新車が、 2つのドアの後ろにはヤギ(はずれを意味する)がいる。 プレイヤーは新車のドアを当てると新車がもらえる。 プレイヤーが1つのドアを選択した後、モンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。 ここでプレイヤーは最初に選んだドアを、残っている開けられていないドアに変更しても良いと言われる。 プレイヤーはドアを変更すべきだろうか?
| クイズ番組に化けているか |
番組最後のゲームと 勘違いしているか |
賞品をどこに隠すか | 賞品構成 | 固有名詞を使っているか | 挑戦者になったつもりで問題を解くよう指示しているか | ホストの行動ルールに関する既述 | 標準仮定の明確度 | 確率数値を問うているか | 選んだ扉や開けた扉を特定するような表現をしているか |
|---|---|---|---|---|---|---|---|---|---|
| 番組の種類不明 | 番組の最後かどうか言及なし | 扉 |
当りの扉に新車 その他の扉にハズレを意味するヤギ |
いる | いない | プレイヤーが1つのドアを選択した後、モンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。 | "Ask Marilyn"並 | いない | いない |
他の言語のWikipediaがこぞって"Ask Marilyn"の問題文を採用している中で、日本語版のように独自の問題文を採用しているWikipediaは国際的に少数派である。(2011年4月28日 現在)
その他の言語のWikipediaのモンティ・ホール問題の記事における"Ask Marilyn"の問題文への切り替え時期
| 言語 | 初版 | "Ask Marilyn"への切替時期 |
|---|---|---|
| ドイツ語 | 17. April 2002 um 04:15 | 29. Oktober 2010 um 20:03 |
| スペイン語 | 2004/09/30 12:36:00 | 初版から |
| 中国語 | 2005年7月23日 15:03 | 初版から |
| フランス語 | 31 juillet 2005 à 16:36 | 初版から |
| イタリア語 | 20:46, 11 set 2005 | 12:20, 12 set 2005 |
| オランダ語 | 5 nov 2005 om 01:32 | 21 feb 2009 om 22:45 |
| ロシア語 | 0014, 24 июля 2005 | 2136, 23 ноября 2006 |
| デンマーク語 | 9. jan 2006, 2357 | 14. nov 2007, 1749 |
| ポルトガル語 | 00h16min de 7 de julho de 2006 | 2011/5/11現在未切替 |
| ポーランド語 | 15:14, 5 sty 2006 | 2011/5/11現在未切替 |
| 韓国語 | 2006年10月7日 00:59 | 初版から |
| インドネシア語 | 17:07, 15 Mei 2008 | 初版から |
| トルコ語 | 15:02, 21 Nisan 2010 | 初版から |
イタリア語版が僅か一日で切り替わったことや、ドイツ語版の切替が遅れたことが興味を引く。
モンティ・ホール問題がでっち上げだった可能性
モンティ・ホール問題の歴史上重要な問題文は次の3つである。
| Steve Selvin の問題文 | モンティ・ホール問題の元祖 | |
| Barry Nalebuff の問題文 | "Ask Marilyn"の問題文の原型 | |
| Craig F. Whitaker の問題文 | "Ask Marilyn"でモンティ・ホール問題を世界的にした問題文 |
ところがよく調べて見ると、これらの問題文がでっち上げである可能性が出て来る。
- ◇モンティ・ホール問題に関する発言を求められたMonty Hall は一貫して、似たようなゲームをしたことがあるともないとも発言していない。
- ◇モンティ・ホール問題のゲームに似たゲームを Let's Make A Deal で見たという証言にめったに出会わない。
Wikipedia(英語版)の "Let's Make A Deal"の記事や、Friedman の論文が数少ない例外 - ◇上記の問題文と同時期の Let's Make A Deal のビデオをインターネットで見ても、それらしきゲームをやっていない。
調べれば調べるほど、Steve Selvin が Let's Make A Deal のゲームと3囚人問題を合成してモンティ・ホール問題をでっち上げたという疑惑が強くなる。
問題文の中のゲームとLet's Make A Deal のゲームが似ているか否かの調査結果
◇ Steve Selvin の問題文の中のゲームの場合
| 資料 | 出典 | 問題文の中のゲームがでっち上げか否かに関する事項 | でっち上げの可能性を高めたか |
|---|---|---|---|
| Steve Selvin の問題文の内容や、作者本人の言葉 | Selvin, Steve (1975a). |
①問題文の冒頭の"It is "Let's Make A Deal" -a famous TV show starring Monte Hall."という文を見ると、Let's Make A Deal で実際に行われたゲームについて書いているように思える。 ②ゲームの進め方を別にすると、ホストと挑戦者の間の会話の描写が、当時の番組のビデオの中の Monty Hall と挑戦者の間の会話の雰囲気とよく合っている。 |
でっち上げの可能性をやや低める |
| Steve Selvin に意見を求められた Monty Hall の返事(1975) | Monty Hall(1975). |
①Steve Selvin が問題文を Monty Hall に送ったことは、実際のゲームと問題文の中のゲームがかけ離れていないことを示唆している。 ②Monty Hall が返した返事の中の、 "The big hole in your argument of problems is that once the first box is seen to be empty, the contestant cannot exchange his box. " は実際のゲームと Steve Selvin のゲームが別物であることを示唆している。(←2015/10/18 修正) ③返事の中に、 "And if you ever get on my show, the rules hold fast for you -- no trading boxes after the selection. " と書かれているので、問題文のゲームに似たゲームを実際に行うことがあり得ると Monty Hall 本人が思っているらしい。 ③返事の中で、Steve Selvin が見たであろう実際のゲームに触れていないが、番組では毎回異なるゲームを行っているので、 Monty Hall 本人がよく覚えていなくても不思議でない。 |
なんとも言えない(←2015/10/18 修正) |
| Let's Make A Deal の公式サイトの "Show Info"のページ |
Let's Make A Deal の公式サイトの "Show Info"のページ (2012/01/03現在) |
Prizes were disguised so that Traders were never sure whether ~途中省略~, or which of three envelopes contained $1,000. という文章がある。 |
でっち上げの可能性をやや低める |
| Wikipedia(英語版)の "Let's Make A Deal"の記事に書かれている内容 | Wikipedia(英語版)の"Let's Make a Deal"の記事(2010年11月26日 21:36の版) | Wikipedia(英語版)の "Let's Make A Deal"の記事に、Steve Selvin の問題文に良く似ているゲームが"Games of chance" として2種類紹介されている。 | でっち上げの可能性をやや低める |
|
インターネットで見ることのできるLet's Make A Deal のビデオ (1975年ごろ) (Steve Selvin が見たであろうTV放送の時期について、注参照) |
http://www.youtube.com |
下記のように Steve Selvin の問題文のゲームによく似ているものがあった。 ゲームの手順 ①5つの品物のうち、99セントのものを当てればシボレーをもらえる。 |
でっち上げの可能性をやや低める。 |
|
Steve Selvin の問題文のゲームのように ①開始時点で当り賞品が何か挑戦者に伝える ②当り以外の2つともハズレである ③ハズレには賞品が無い という特徴を持ったゲームは、私が見た範囲には無かった。 |
でっち上げの可能性をやや高める。 | ||
| 3囚人問題の問題文との類似性 |
市川 伸一, 下條 信輔. (2010). Selvin, Steve (1975a). |
市川 伸一, 下條 信輔. (2010).で紹介されている3囚人問題の問題文の最後で、囚人Aが自分が恩赦になる確率が 1 / 2 になったと述べ、 Selvin, Steve (1975a).の問題文では ホストが挑戦者に対して、挑戦者が持っている箱が当りの確率は 1 / 2 だと述べている。 | でっち上げの可能性をやや高める。 |
| Selvin, Steve (1975a).では、問題文に続けて解答も書かれているが、3囚人問題への言及がない。 | でっち上げの可能性をやや低める。 |
注: Steve Selvin が彼の問題文の中のゲームに良く似たゲームを Let's Make A Deal で見たことがあるならば、それは次のいずれかであろう。
1968/10/30~1976/7/9 ABC の Daytime や Primetime にて放送
1971/9/18~1977/5/28 Nighttime Syndicated にて放送
◇ Baryy Nalebuff の問題文の中のゲームの場合
| 資料 | 出典 | 問題文の中のゲームがでっち上げか否かに関する事項 | でっち上げの可能性を高めたか |
|---|---|---|---|
| Barry nalebuff の問題文の内容(前掲の問題文参照) | Nalebuff, Barry (1987). |
①Host Monty Hall asks contestants to choose the prize behind one of three curtains. Behind one curtain lies the grand prize;the other two curtais conceal only small gifts. という文から、番組最後の"big deal of the day" をモンティ・ホール問題のゲームのモデルだと勘違いしている可能性が高い。 ②Now, Monty must know what lies behind all three curtains, because never in the history of the show has he ever opende up an unchosen curtain to reveal the grand prize. という文は、確率計算に必要な条件を明確化するために付け加えた創作である可能性が高い。 |
でっち上げの可能性を高める |
| Friedman が Barry Nalebuff から聞き出した言葉(注参照) | Friedman, D. (1998). | Nalebuff の言葉は、彼 が Let's Make A Deal を注意深く見ていなかったことを示している。 | なんとも言えない |
|
インターネットで見ることのできるLet's Make A Deal のビデオ(1987年ごろ) (Barry Nalebuff が見たであろうTV放送の時期について、注参照) |
http://www.youtube.com |
何本か見たビデオの中に、Barry nalebuff の問題文のゲームとやや似ているゲームがあった。 ゲームの手順 ①現金の箱と「乗り物」と書かれた扉1から選択 |
なんとも言えない |
注: Friedman はNalebuff から次の言葉を聞き出している。
注: Barry Nalebuff が彼の問題文の中のゲームに良く似たゲームを Let's Make A Deal で見たことがあるならば、それは次のいずれかであろう。Nalebuff says he personally recalls watching the show and seeing the switch option offered (as do I), but he cannot recall "whether Monty offered this option all the time and whether or not his making the offer was at all connected to whether you picked the right door." ---Friedman, D. (1998). から
1980/9/29~1981/7/14 Syndicated にて放送
1984/9/17~1986/9/12 Syndicated にて放送
◇ Craig F. Whitaker の問題文の中のゲームの場合
"Ask Marilyn" でモンティ・ホール問題が取り上げられた時期は "Let's Make A Deal" の放送が再開された時期でもある。
しかし、 Lane Pageという人による Craig F. Whitaker さんへの取材記事を読むと、"Ask Marilyn"に問題文を投稿した時期と、Let's Make A Deal が放送されていなかった時期が重なる可能性が高い。Page, Lane (2005).
注: "Ask Marilyn"で議論をしていた読者たちがAsk Marilyn"の問題文の中のゲームに良く似たゲームを Let's Make A Deal で見たことがあるならば、それは次の放送であろう。
しかし、 Lane Pageという人による Craig F. Whitaker さんへの取材記事を読むと、"Ask Marilyn"に問題文を投稿した時期と、Let's Make A Deal が放送されていなかった時期が重なる可能性が高い。Page, Lane (2005).
| 資料 | 出典 | 問題文の中のゲームがでっち上げか否かに関する事項 | でっち上げの可能性を高めたか |
|---|---|---|---|
| インターネットで見ることのできるLet's Make A Deal のビデオ(1975~1990年ごろ) | http://www.youtube.com |
見ることのできた映像の中では、Zonk賞品(冗談賞品)が 2つのカーテンや扉に置かれていたケースは皆無。 仮にZonk賞品が2箇所に置かれているケースがあったとしても、両方ともヤギにするとは考えにくい。 |
でっち上げの可能性を高める |
| "Ask Marilyn"の問題文に対する Monty Hall の意見(1991) | Tierney, John (1991). |
New York imes のJohn Tierney の取材の中で Monty Hall は "Ask Marilyn" の問題文の中のゲームに似たゲームを行ったことがあるのかないのか、まったく触れていない。 |
でっち上げの可能性をやや高める |
| "Ask Marilyn"の問題文に対する世間の反応(1991年以降) | もろもろの資料 |
"Ask Malilyn"の問題文も、当時放送されていた Let's Make A Deal も有名であったので、ゲーム内容に類似点があれば、何かの資料で読むことができるだろうが、そのような資料に出会うことがない。 |
でっち上げの可能性をやや高める |
| Let's Make A Deal の公式サイトでのモンティ・ホール問題の扱い |
Let's Make A Deal の公式サイトの "Monty Hall Problem "のページ (2010/10/11現在) |
モンティ・ホール問題に関するページの中で "Ask Marilyn"の問題文を紹介しているが、それに対応する Let's Make A Deal のゲームがどのようなものか書いていない。 | でっち上げの可能性をやや高める |
注: "Ask Marilyn"で議論をしていた読者たちがAsk Marilyn"の問題文の中のゲームに良く似たゲームを Let's Make A Deal で見たことがあるならば、それは次の放送であろう。
1990/7/9~1991/7/11 NBC Daytime にて放送
モンティ・ホール問題のゲームがでっち上げか否かに関する調査結果のまとめ
上記のような調査結果から、モンティ・ホール問題は、Stebe Selvin がたまたま見たある日のあるゲームに関する問題であったものが、Baryy Nalebuff 、Craig F. Whitaker へと受け継がれていく間に、賞品の隠し場所や ハズレ賞品の内容について創作が加わったものだと言えそうである。
私の想像によると、次のように問題文が変容して行ったのだろう。(あくまでも私の想像である)
私の想像によると、次のように問題文が変容して行ったのだろう。(あくまでも私の想像である)
◇ Steve Selvin の問題文の中のゲームの場合
次のことから、Steve Selvin の問題文のように三つの箱を使ったゲームを Steve Selvin がたまたま見た放送でやっていて、たまたまそのときは、箱を switch する機会が挑戦者に与えられていた可能性がある。
- Steve Selvin の問題文の中のゲームの情景は U-Tubeで見ることのできる映像の情景と雰囲気が似ている。
- Monty Hall の手紙の内容から判断して、挑戦者にSwitch の機会が与えられることもあったらしい。
- Let's Make A Deal の公式サイトの "Show Info"のページに「三つの封筒」という言葉が見える。
- 映像資料を見る限り、ゲーム開始時点で賞品のリストを示すような展開を見たことが無い。
- 映像資料を見る限り、Let's Make A Deal で同じゲームが別の放送で繰り返して行われた形跡もない。
◇ Baryy Nalebuff の問題文の中のゲームの場合
Baryy Nalebuff は あくまでも Steve Selvin の問題文の中のゲームを下敷きにして、箱やカーテンなどの小道具、大道具を当時の Let's Make A Deal に合わせて書き変えただけであり、ゲームの進め方には手を着けていないのだろう。
(あくまでも私の想像である)
(あくまでも私の想像である)
◇ Craig F. Whitaker の問題文の中のゲームの場合
Lane Pageという人による Craig F. Whitaker さんへの取材記事 (Page, Lane (2005). ) を読むと、"Ask Marilyn"に問題文を投稿した時期と、Let's Make A Deal が放送されていなかった時期が重なる可能性が高い。そして Craig F. Whitaker さんは Monty Hall が何者か知らなかったため、Baryy Nalebuff の問題文から固有名詞を省いたのかも知れない。
Zonk 賞品としてヤギを採用したのは、Let's Make A Deal を見たことのある友人などから聞いた話を元に作り出した創作かも知れない。
(あくまでも私の想像である)
Zonk 賞品としてヤギを採用したのは、Let's Make A Deal を見たことのある友人などから聞いた話を元に作り出した創作かも知れない。
(あくまでも私の想像である)
Monty Hall が「地獄から来たMonty」かどうかは心配無用
下記の資料を読むと、Monty Hall が挑戦者が当たりを選んだときだけ switch の機会を与える「地獄から来たMonty」だったのかと心配になる。しかし、モンティ・ホール問題のゲームに良く似たゲームがLet's Make A Deal で行われたことはほとんど無いことや、Monty Hall がアドリブでゲームを進めているらしいことから、Monty Hall が「地獄から来たMonty」かどうか心配しても意味がない。
Monty Hall(1975).
Steve Selvin から小論 "A Problem in Probability" を 受け取った Monty Hall が返した返事を Let's Make A Deal の公式サイトで見ることができる。その中に「地獄から来たMonty」を思わせる既述がある。
"The big hole in your argument of problems is that once the first box is seen to be empty, the contestant cannot exchange his box."
1991年に Monty Hall に取材した New York imes のJohn Tierney が次のように書いている。
Not according to the rules of the show, because he did have the option ofnot offering the switch, and he usually did not offer it.
1987年にBarry Nalebuff がLet's Make A Deal のゲームのTV放送を観て作った問題文を題材に論じている。そして、Monty Hall 本人や Nalebuff などに、実際の Monty Hall の行動を問い合わせ、Monty Hall 本人からは、滅多にswitchの提案をしなかったことを聞きだしている。Let's Make A Deal の制作アシスタントの Carol Andrews からは、Monty Hall が switch の提案をしたことは無いと聞き出している。
Nステージ問題 – モンティ・ホール問題をより現実のゲームに近づけようとする試み –
Rao, M. Bhaskara. (1992). は "Comment on Morgan et al."( American Statistician, 46, 241-242.)で、次のようなゲームを考察している。
・ドアが4つ(当たりが一つ、ハズレが三つ)ある。
・最初に挑戦者が選ぶ。ホストが残りの三つの中からハズレ扉を一つ開ける。
・ホストが残りの中からハズレ扉を一つ開ける。
・挑戦者に扉を switch する機会があたえられる。
・挑戦者の決定後、ホストが残りの二つの中からハズレ扉を一つ開ける。
・挑戦者に扉を switch する機会があたえられる。
これは、私が U-Tube で観た Let's Make A Deal の実際のゲームに似たところがある。
それらのゲームでは、{現金、大当たりのドア、中当たりのドア、Zonk(冗談賞品)のドア} のような組合せだったりして、{当たり、ハズレ、ハズレ、ハズレ}のような組合せは皆無であるが、段階ごとに一つずつ開けていくという点で、Rao さんの考えたゲームに似たところがある。
Rao さんも熱心に Let's Make A Deal のTV放送を観たのだろう。
(あくまでも私の想像である)
Rosenhouse, Jason.(2009). の中には、このNステージ問題で、最後に一度だけ switch するのがベストだということを数学的帰納法で導いている箇所がある。 扉の枚数が5枚以上の一般論を知りたい人には、Bapeswara Rao, V. V. and Rao, M. Bhaskara (1992). を入手するより、この本を読む方が手軽でしょう。
モンティ・ホール問題が有名になるきっかけとなった "Ask Marilyn" での大論争
1990年9月から半年以上に渡って繰り広げられた"Ask Marilyn"での大論争は、モンティ・ホール問題を世に広めるきっかけになっただけあって、その経緯自体が興味深い。PARADE という日曜ニュース雑誌のコラム"Ask Marilyn" に Craig F.Whitaker という人が投稿した問題に対して「挑戦者が選ばなかった扉が当たりの確率は2/3である」と Marilyn vos Savant が回答したことが騒動の発端である。1990年9月9日(日曜)のことであった。(vos Savant, Marilyn (1990).)
PARADE誌は数百の新聞に配信されていたらしい。
彼女の回答に対して大勢の読者から続々と反論の投書が寄せられ始めたので、12月に"Ask Marilyn"でふたたび取り上げて説明を試みたが、反論の投書が止まず、翌年の2月に実験を提案して"Ask Marilyn"での議論を打ち切った。(vos Savant, Marilyn (1990b).;vos Savant, Marilyn (1991).)
その後、多数の教育機関で実験が行われ、彼女の答えの正しさが知れ渡ると同時に、反論の投書も減り始めた。実験結果に驚嘆した数学教師からの賞賛の手紙や、実験結果を発表して賞をもらった学生や小学生からの感謝の手紙が、Marilyn vos Savant により発表されている。
1991年7月21日 の New York Times 日曜版で特集記事(Tierney, John (1991).)が組まれるに至ったのは、多数の博士達に素人女性が勝ったというセンセーションが New York Times の John Tierney の耳に入ったためだろう。その記事によると
PARADE誌は数百の新聞に配信されていたらしい。
彼女の回答に対して大勢の読者から続々と反論の投書が寄せられ始めたので、12月に"Ask Marilyn"でふたたび取り上げて説明を試みたが、反論の投書が止まず、翌年の2月に実験を提案して"Ask Marilyn"での議論を打ち切った。(vos Savant, Marilyn (1990b).;vos Savant, Marilyn (1991).)
その後、多数の教育機関で実験が行われ、彼女の答えの正しさが知れ渡ると同時に、反論の投書も減り始めた。実験結果に驚嘆した数学教師からの賞賛の手紙や、実験結果を発表して賞をもらった学生や小学生からの感謝の手紙が、Marilyn vos Savant により発表されている。
1991年7月21日 の New York Times 日曜版で特集記事(Tierney, John (1991).)が組まれるに至ったのは、多数の博士達に素人女性が勝ったというセンセーションが New York Times の John Tierney の耳に入ったためだろう。その記事によると
- 〇Marilyn vos Savant は約1万通の反論の手紙を受け取り、そのうち、博士号取得者(多くは数学または科学の)からのものが約千通にのぼった。
- 〇CIAのいくつかのホール(廊下?)で討論された。
- 〇ペルシャ湾の戦闘機パイロットも討論した。
- 〇マサチューセッツ工科大学で分析された。
- 〇ロスアラモスの国立研究所の計算機で分析された。
- 〇Marilyn vos Savant の提案を受けて、小学生から大学生まで、全米にまたがる1000以上の学校で実験が行われた。
- 〇Monty Hall も Marilyn vos Savant の答えの正しさを認めている。
- 〇Marilyn vos Savant に反論した学者達の多くも、最終的に彼女が正しいという結論に達した。
- 〇その中のSachs博士から Marilyn vos Savant宛てに敗北宣言の手紙が書かれた。
- 〇Marilyn vos Savantのコラムを読んだ Monty Hall が次のようなパターンを提示した。
挑戦者がハズレを選んだとき、すぐにその扉を開いてハズレだと伝えてから、ゲームをやり直させ、 次に挑戦者が当たりを選んだとき、ハズレの扉を開いてから、挑戦者に、stay するか、switch するか、 あるいは5千ドルと交換するかを選ばせる。 このようなパターンの場合、自動車を得るには switchしてはいけなことを、Manty Hall が実際にやって見せた。 - 〇Monty Hall はめったに挑戦者に switch させなかった。(注参照)
- 〇Martin Gardner が問題文の曖昧さを指摘した。
- 〇問題文は確かに曖昧であるが影響はなかったと Mailyn vos Savant が反論した。
- 〇Monty Hall の言葉でしめくくり。
「もしも、5千ドルとの交換を私に提案させることができたら、扉を開けずにお金を持って帰りなさい」
番組最後の"big deal of the day"がモンティ・ホール問題のゲームのモデルだと、Tierney が勘違いしていて、Monty Hall もそれに話を合わせていた可能性がある。
Marilyn vos Savant の解答の変遷
1990年9月9日号のPARADE 誌上での解答
switch して賞品を得る確率が 2/3 だとしているが理由は述べていない。そのかわり、扉の枚数が百万枚に増えたときのことを想像すれば納得がいくだろうと述べている。
1990年12月2日号のPARADE 誌上での解答
「非条件付確率の問題設定(挑戦者が選んだ扉を扉1に限定)」の解を、等確率の場合分けの方法で導いている。
1991年2月17日号のPARADE 誌上での解答
「非条件付確率の問題設定(挑戦者が選んだ扉もランダム)」での実験を提案している。
実験の内容は紙コップと硬貨を使って、二人がかりで実験し、データを記録して、switchする戦略で賞品を獲得する確率とstayする戦略で賞品を獲得する確率を計算するというものである。
実験の内容は紙コップと硬貨を使って、二人がかりで実験し、データを記録して、switchする戦略で賞品を獲得する確率とstayする戦略で賞品を獲得する確率を計算するというものである。
Marilyn vos Savant の解答は正しかったのか
正しい①
彼女が 1991年2月17日号のPARADE誌で提案した実験は標準仮定を前提としたものであるが、その結果に全米の小中高大学生や大学教授たちが驚嘆して彼女に感謝し、さらには彼女に反論した人々の半数から彼女の正しさを認める手紙が来たのだから、標準仮定を前提とした彼女の解答は正しい。
間違っている①
"Ask Marilyn"の問題文には標準仮定が成立しない余地があるにもかかわらず、標準仮定のケースしか答えていないので彼女の解答は不完全である。
正しい②
問題文の質問は証拠事象を特定していない。従って、「非条件付確率の解答」をしている彼女の12月の解答は正しい。
間違っている②
問題文の質問はホストが扉3を開いたことを証拠事象とする確率を求めている。従って、彼女の「非条件付確率の解答」は誤りである。
正しい③
ホストが扉3を開ける癖があったなら、switchして賞品を得る確率は 1/2 になってしまうが、最悪でも 1/2 以上なので switch の方が有利であることに変わりはない。設問は switch が有利かどうかを聞いているのだから、彼女の解答は正しい。
間違っている③
ホストが扉3を開ける癖があったなら、switchして賞品を得る確率は 1/2 だから、確率が 2/3 だとする彼女の解答は誤りである。
このような議論は New York Times の特集記事の後すぐに始まり、21世紀になってもまだ続いている。
最近の例としては、Wikipedia(英語版)の"Monty Hall Problem"の執筆者たちに向けて、対称性に基づく解を提案した Richard Gill (2011年2月)の例がある。
彼の説の要旨は次のとおりである。
| 3つの扉の間の対称性により、条件付確率の問題設定を 非条件付確率の問題設定に帰着させることができる。 Marilyn vos Savant の解答が条件付確率の解答になっていないから間違いだと述べる人は、 "Ask Marilyn" の問題文の中で、挑戦者が選んだ扉を扉1に、 ホストが開けた扉が扉3にそれぞれ特定されているかのように書かれていることに惑わされているのだ。 |
Marilyn vos Savant に多くの人たちが反論した理由
次のことが、Marilyn vos Savant の解答に反論が殺到した理由だろう。
- ◇無意識のヒューリスティクが瞬間的に答えを出すので、素人にも解ける問題だと錯覚する。
- ◇Marilyn vos Savant の解答は、日常的に使っているヒューリスティクへの信頼を脅かすものであった。
- ◇そもそも、"Ask Marilyn"は Marilyn vos Savant の解答に反論して楽しむコラムであった。
- ◇Marilyn vos Savant は間違えることもある。 現に、Craig F. Whitaker さん (モンティ・ホール問題の出題者) が出した別の問題に間違えたことがある。
- ◇"Ask Marilyn"で取り上げられた時期は、"Let's Make A Deal"のTV放送が再開されたばかり(2ヶ月後)であったため興味を引いた。
- ◇Marilyn vos Savant の扉の数を百万枚に増やした場合を想像する説明が数学的に無意味なものだった。
- ◇Marilyn vos Savant の 1990年12月の説明も 非条件付確率の解答に過ぎず、特定事象による条件付確率あるいは事後確率の解答になっていなかった。
- ◇Marilyn vos Savant は一貫して 「戦略」 (switch する戦略と switch しない戦略) に着目して説明しているため、 日常的な確率概念のもとに 「扉」 に着目して考える人々 (数学者含む) から見てうさんくさく見えた。
- ◇条件付確率や事後確率に関する詳しい教育を、当時の数学者の多くが受けていなかった。
- ◇Marilyn vos Savant が科学者たちから嫌われていた。
※ポール・ホフマン著「放浪の天才数学者エルデシュ」によると、アインシュタインなどの有名な理論に異を唱える Marilyn vos Savant に対して、多くの学者が反感を持っていたらしい。
"Ask Marilyn" の問題文の曖昧さは、反論が殺到したことと関係がない
von Randow(1993)は、"Ask Marilyn"の問題文で挑戦者が当たりを選んだときのホストの行動ルールの情報がないことが低い正答率の説明になると述べているらしい。(Krauss and Wang(2003)による)
Wikipedia(日本語版)の「モンティ・ホール問題」の記事は"Ask Marilyn"の問題文の曖昧さが原因で反論が殺到したとしている。(2010年8月8日現在)
しかし、このような説はデマである。
その根拠をいくつか列挙する。
Wikipedia(日本語版)の「モンティ・ホール問題」の記事は"Ask Marilyn"の問題文の曖昧さが原因で反論が殺到したとしている。(2010年8月8日現在)
しかし、このような説はデマである。
その根拠をいくつか列挙する。
〇標準仮定を読み取るか否かと、正答するか否かとの間に因果関係はない
標準仮定を意識させるような問題文を使っても使わなくても、正答率に大きな差がないことが心理学的研究によって明らかになっている.
◇ 市川 伸一, 下條 信輔. (2010).の実験
◇ 市川 伸一, 下條 信輔. (2010).の実験
囚人Aが恩赦になるときに看守が囚人BとCのどちらの運命を囚人Aに伝えるかという選択確率を意識させるような問題文を使った実験を行って、選択確率の知識があってもそれをうまく活用できなかったという、研究成果を、「3囚人問題研究の展開と意義をふり返って」の中で紹介している。
◇ Granberg らの実験
Krauss, Stefan and Wang, X. T. (2003). によると、Granberg らは実験で、「モンティは必ず挑戦者が選ばなかったハズレのドア開ける」という文言を加えた問題文を使ったが、被験者のたった 13% しかswitchを選択しなかった。
Krauss, Stefan and Wang, X. T. (2003).は実験で「等確率開扉の仮定」以外の標準仮定を明記した問題文を使ったが確信を持って switch の方が有利だとしている回答は 5~6% にとどまっている。
◇ De Neys, W. & Vershueren, N. (2006). が報告している実験
Krauss, Stefan and Wang, X. T. (2003). が実験で使った「等確率開扉の仮定」以外の標準仮定を明記した問題文をベースに作った問題文を使った実験の結果、大学生の 5.2% が switch と答えている。
〇"Ask Mariylyn"の問題文から標準仮定を読み取らない人は少ない
Mrilyn vos Savant に反論した人の大部分が "Ask Marilyn"の問題文から標準仮定を読みっていたことを示す根拠がある。
◇ "Ask Marilyn"の問題文よりあいまいなシナリオでも、標準仮定を読み取る人の方が多い。
◇ "Ask Marilyn"の問題文よりあいまいなシナリオでも、標準仮定を読み取る人の方が多い。
映画「ラスベガスをぶっつぶせ」( 原題 "21" )の中の モンティ・ホール 問題の授業のシーンや、2010年1月3日の平成教育委員会のお年玉の袋3つを使った問題の授業では、ホストの行動ルールについての説明が貧弱であるが、Yahoo! Answers やYahoo!知恵袋などのQAサイトでこれらの映画や番組に関する記事を見ると、標準仮定に依拠した説明を読んだ質問者の多くが、その説明に納得している。
◇ Marilyn vos Savant の Webページによると、ホストが意図的にハズレの扉を開けると読み取った読者が大勢を占めていることが書かれている。
◇ Wikipedia(英語版) の "Monty Hall problem" の記事 (20:04, 18 December 2012 の版) によると vos Savant, Marilyn (1996).に、 "Ask Marilyn"の問題文を読んだ人の多くが標準仮定を読み取ったことが報告されている。
〇"Ask Marilyn"でMarilyn vos Savant に反論した人たちが取った行動は上記を裏付けている
◇ Tierney, John (1991). によると、 Marilyn vos Savant に反論した数学者の Sachs 博士が自分の誤りを認める手紙を彼女に送っている。
その中で彼は次のような興味深い英語の慣用句を使っている。
"telling her that after removing my foot from my mouth I'm now eating humble pie."
"telling her that after removing my foot from my mouth I'm now eating humble pie."
◇ Marilyn vos Savant の Webページによると、"Ask Marrilyn"で反論が公開された読者の半分から自分の誤りを認める手紙が来たそうである。
〇3囚人問題でも正答率は似たり寄ったりである
◇ 3囚人問題は標準仮定の曖昧さがモンティ・ホール問題より少ないが、誤答する人の割合は似たり寄ったりである。
仮にこれらの根拠がなかったとしても、問題文の曖昧さが低い正答率の説明になるという説がデマであることが次のようにしてわかる。
標準仮定と異なる仮定を想定して switch してもしなくても同じだと判断したプロセスが数学的な思考プロセスによるものだとしたら、標準仮定が成立する場合には結果が異なること(あるいは異なるかも知れないこと)に気付くのは容易である。
しかし switch してもしなくても同じだと判断した人たちはそこまで至っていないので、彼らの思考プロセスは無意識に自動起動されたヒューリスティクによるものに他ならない。
無意識に自動起動されるヒューリスティクのロジックは標準仮定が成立するか否かを考慮するような高度なものではないので、標準仮定を明記しても正答率は簡単には上がらない。
ワーディングの議論
標準仮定がワーディングの議論の的になる理由
モンティ・ホール問題や3囚人問題を解くには 標準仮定を確認することが必要になる。 ということはとりもなおさず、標準仮定に議論の余地があることを意味している。
大多数の人が無意識に仮定し、それでいながら結果の確率を左右する重要な仮定であることが、「標準仮定」がワーディングの議論の的になる理由だろう。
大多数の人が無意識に仮定し、それでいながら結果の確率を左右する重要な仮定であることが、「標準仮定」がワーディングの議論の的になる理由だろう。
標準仮定を無意識に仮定する理由
私は次のような性質を確率判断のヒューリスティクが次のような性質を持っていて、それが標準仮定を無意識に仮定する原因になっていると考えている。
◇ 確率の違いに関する情報や知識の無い事象に等確率を割り付ける。
◇ 可能性に言及されていない事象は発生しないものと仮定する。
◇ 確率の違いに関する情報や知識の無い事象に等確率を割り付ける。
◇ 可能性に言及されていない事象は発生しないものと仮定する。
ワーディングの議論の例
"Ask Marilyn"の論争の後でしばらくの間、"Ask Marilyn"の問題文は曖昧であるとする立場に立って、標準仮定以外の条件での確率を検討する議論、すなわち「ワーディングの議論」が盛んに行われたことが、下記の資料からわかる。
これらであげられたものを年代順に列挙する。
- ◇ 三好一英・服部環 (2009).
- ◇ Krauss, Stefan and Wang, X. T. (2003).
- ◇ Tierney, John (1991).
- ◇ Wikipedeia(英語版)の"Monty Hall problem"の記事
- ◇ American Statistician のデジタルアーカイブ
これらであげられたものを年代順に列挙する。
| ワーディングを論じた人や文献 | 私が参照した文献 | 主張内容 | ワーディングを論じた動機 |
|---|---|---|---|
|
Diaconis (有名な統計数学者で手品師) |
Tierney, John (1991). | ホストの行動の意図を知らなければ確率を求めることはできないと述べている。 | 不明 |
| Martin Gardner | Tierney, John (1991). | もしもホストが maleover なら、プレイヤーが switch することがホストの利益になるときしか他の扉を開けないだろから、switch で賞品を得る確率は限りなくゼロに近いと述べている。 | 不明 |
|
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). "Let's Make A Deal: The player's dilemma," American Statistician 45: 284-287. |
同左 |
・Marilyn vos Savant の解答で想定している標本空間は、条件付き確率の解答を出せるような標本空間ではないので彼女の解答は"wrong"だとしている。 ・その根拠として、挑戦者が当たりの扉を選んだときにホストが開く扉に偏りがあるケースを論じている。 |
数学者によるワーディングの議論の項参照 |
|
Gillman, Leonard (1992). "The Car and the Goats," American Mathematical Monthly 99: 3-7. |
同左のページ3 | 挑戦者が当たりの扉を選んだときにホストが開く扉に偏りがあるケースを論じている。 | 数学者によるワーディングの議論の項参照 |
| Bell, William (1992). Comment on Let's make a deal by Morgan et al., American Statistician 46(3): 247 (August 1992). | 同左 | ホストが開ける扉の好みを反映しない Marilyn vos Savant の解は"wrong"だとする Morgan らの説を受けて、扉1が当たりである事象と、ホストが扉3を開ける事象が独立だと言う判断が直感的に明らかなら、Marilyn vos Savant の解答も reasonable だとしている。 | 数学者によるワーディングの議論の項参照 |
|
Klein, I. (1993), Comment on Morgan et al. American Statistician, 47, 82-83. |
同左 | conditional solustion と unconditional solution の答えが一致する条件式を求めている。 | 数学者によるワーディングの議論の項参照 |
| von Randow, G.(1993).Das Ziegenproblem: Denken in Wahrscheinlichkeiten. Reinbeck, Germany: Rowohlt Verlag. | Krauss, Stefan and Wang, X. T. (2003). | "Ask Marilyn"の問題文で挑戦者が当たりを選んだときのホストの行動ルールの情報がないことが低い正答率の説明になることや、"Ask Marilyn"の問題文に当たり扉の配置の確率が明記されていないことなどを指摘しているらしい。 | 数学者によるワーディングの議論の項参照 |
| Nickerson, R.S. (1996. Ambiguities and unstated assumptions in probabilistic reasoning. Psychological Bulletin, 120, 410-433., | Krauss, Stefan and Wang, X. T. (2003). |
次のようなことを書いているらしい。 ・ホストの行動に関する情報もしくは仮定がなければ、switch すべきか否かは決められない。 ・当たり扉の配置の確率が"Ask Marilyn"の問題文に明記されていない。 |
ちょっとした条件の違いが大きな確率の違いになることの例としてモンティ・ホール問題を取り上げたため、ワーディングを論じたものと思われる。 |
|
Mueser, Peter R. and Granberg, Donald (May 1999). ※1999年という遅い時期にワーディングを論じている |
同左 |
"THE HOST'S PROTOCOL AND THE GENERAL SOLUTION" という章の冒頭で次のように書いている。 ・問題文にはホストの行動様式がほとんど書いてない。 ・特に、 挑戦者が選ばなかった中からハズレの扉を開けること、 挑戦者が当りを選らんだとき残りの扉を等確率で開けること、 および、 賞品の配置が3つの扉に等確率で配置されることについて何も書かれていない。 |
Granberg, Donald and Brown, Thad A. (1995). の流れをくんだ実験を行っている。 ホストがあてずっぽうに扉を開けてしまう問題文や、ホストが挑戦者に協力的だったり非協力的だったりする問題文で実験を行っている。 |
ワーディングを論じる意義はあるのか
ワーディングを論じる意図が次のようなものであれば、論じることにも意義がある。
- ◇Steve Selvin の問題文や Craig F. Whitaker の問題文など主要な問題文の既述だけでは数学の問題として "well defined" でないので、数学の問題として議論するときはしっかり前提条件を明らかにしよう。
- ◇モンティ・ホール問題の問題文の曖昧さを操作して、問題文の曖昧さと正答率の間に関係があるか研究しよう。
- ◇確率に関する状況描写を聞いたり読んだりしたときに、確率に大きな違いのでるような仮定を無意識にすることがあるので気をつけよう。
- ◇先刻承知確率不変説の過剰適用 の誤りを説明するために 等確率開扉の仮定 が成り立たないケースを材料にしよう。
次のような意図で論じるのであれば、特に問題はない。
- ◇問題文の曖昧さは即ち、素事象の確率値の範囲が決まっていないことだと解釈して、素事象の確率値に関する方程式を立て、 扉をswitch した方が有利になる条件や、質問した囚人の恩赦確率が上がらない条件などを示してみよう。
しかし、次のような議論には無理がある。
- ◇Marilin vos Savant の説明のような 非条件付確率の問題設定 が不完全であることを示すために、 特定事象による条件付確率あるいは事後確率の問題設定 と答えが食い違うケースを色々取り上げよう。
このような議論の無理は次のとおり。
- 挑戦者が選んだ扉が当たりのときだけホストが他の扉を開けるなどという条件にすると単純になりすぎて面白みがない。
- 挑戦者が選んだ扉が当たりのときにホストが開ける扉に好みがある条件にしても、 好みがない標準的な条件と比べて錯覚に基づく解答の間違いを示す力に優劣がない。
- 当りの扉が一つしかないのにホストが当たり扉を開けてしまうことがあるという意地悪な条件では、テレビ番組らしくなくなってしまう。
- 当たり扉の配置やホストの行動パターンに関する仮定の中で、標準仮定は最も秩序立った仮定の1つであり、 当たり扉の配置やホストの行動パターンに何の制約も無い仮定は最も乱雑な仮定である。 ワーディングを議論する人は、これらの中間にある仮定を取り上げて確率を計算していることになるか、あるいは、挑戦者が当りを選んだときだけホストが扉を開けるなどといった、 秩序高くても問題文から読み取りにくい仮定を取り上げて確率を計算していることになる。 そんな計算などしなくても、「仮定によって確率は異なる」 の一言で済むのではないだろうか?
次のような議論にも無理がある。
- ◇残った扉が当りである確率がどちらも
1/2 だと考えてもおかしくないこと訴えるために問題文の曖昧さを取り沙汰しよう。
このような議論の無理は次のとおり。
- 確率の手掛かりが無い場合に、おこりうるケースすべてに同じ確率を割り振るのは日常の確率概念の世界の話であり、数学パズルであるモンティ・ホール問題に当てはめようとするのは、すじ違いである。
- そこまでして確率 1/2 を復活させようとする心理の方が心理学的な研究対象になる。
ワーディングを論じる論文が出た当時の数学界の状況
状況その1
1975年の"AmericanStatistician"の5月号の目次にベイズ統計の教育に関する特集が組まれていたので、それ以前に教育を受けた数学者の中に、条件付き確率や事後確率の知識の乏しい人がいてもおかしくないことがわかる。
15年後の1990年に "Ask Marilyn"で Marilyn vos Savan に反論した博士たちの中に数学者も含まれていたのは、そのためだろう。
2011年の現代では、書店にベイズ統計学の教科書が並ぶようになっているので、状況が変わっているらしい。
15年後の1990年に "Ask Marilyn"で Marilyn vos Savan に反論した博士たちの中に数学者も含まれていたのは、そのためだろう。
2011年の現代では、書店にベイズ統計学の教科書が並ぶようになっているので、状況が変わっているらしい。
状況その2
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). の論文への "comment" として書かれたSeymann R. G. (1991). "Comment on Let's make a deal: The player's dilemma," の中に、病気を早期発見するための検査結果を見た人がやりがちな確率の錯覚について書かれている。 条件付確率や事後確率の話題が当時の統計数学界を賑わしていたのかも知れない。
状況その3
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). の論文が掲載された "American Statistician"の 同じ号に、この論文に対するSeymann R. G. (1991). のコメントや、vos Savant, Marilyn (1991b).からの返事、それらに対する Morgan らの反論が掲載されて、あたかも誌上討論会のようになっている。このことから、当時の統計数学界でモンティ・ホール問題が大問題になっていただろうことがわかる。
数学者たちがワーディングを議論した動機
Diaconis のような大物数学者を別にして、数学者や数学の学生たちがワーディングを議論した動機として、次のような想像ができる。
あくまでも想像に過ぎないことを、くれぐれも御注意されたい。
◇ 条件付確率や事後確率の話題は当時の統計数学界で論文誌に採用されやすかった。
モンティ・ホール問題が話題になった1991年という時期が、条件付確率や事後確率の話題が統計数学者の関心を引き始めていた時期と重なった。そうした中で、標準仮定の重要性に気付かずに Marillyn vos Savant の受け売りをしている統計数学者もいる状況だったことから、Marillyn vos Savant の解答の不備を指摘するだけでも論文誌に採用される状況であった。 (あくまでも私の想像である)
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). はその格好の事例といえるかも知れない。
彼らの論文"Let's Make A Deal: The player's dilemma," を読むと、次のような趣旨で書かれているように見える。
- Marilyn vos Savant の解答で想定している問題設定では、ホストが開ける扉に偏りがある場合の確率を計算できないことを発見して論文にする価値ありと思った。(あくまでも私の想像である)
- Marilyn vos Savantの解答は"wrong"だとする既述のくどさは、彼女に対する反感から来たものではなく、人々を啓蒙しようという意識から来たものだろう。 (あくまでも私の想像である)
◇ 非条件付確率の問題設定 と 特定事象による条件付確率あるいは事後確率の問題設定 の答えが一致する条件に興味を持った
これらの問題設定ごとの確率が一致する条件を考えるということは、必然的にゲームのルールのバリエーションを考えることになる。一見するとワーディングを議論しているように見えるが、問題設定の間の関連性の検討手段として議論しているだけなのだろう。
Morgan らの論文に触発された下記の議論はその格好の事例である。
①Bell, William (1992).
Morgan らの論文に触発された下記の議論はその格好の事例である。
①Bell, William (1992).
Bell, William (1992). が上の表にあるような議論をしたのは、Marilyn vos Savant の解答で想定している標本空間は不完全"だとする Morgan らの主張に無理を感じたからだろう。(あくまでも私の想像である)
Klein, I. (1993), が上の表にあるような議論をしたのは、Marilyn vos Savant の解答と条件付確率あるいは事後確率の解答が一致する条件について、当たり扉の配置確率やホストが開ける扉の偏りなどをパラメータとする一般式を求めてみたかったのだろう。
◇ 非条件付確率の解答を理解できなかった。
Marilyn vos Savant の非条件付確率の解答は、よほど確率論に詳しくないと居心地の悪いものである。確率判断の無意識のヒューリスティクが、扉3が開かれた時点で無意識に標本空間を切り替えてしまうからである。
また、ホストが開ける扉にくせがあると非条件付確率の解答と特定事象による条件付確率あるいは事後確率の解答で異なる確率値になるが、同一の問題に複数の確率値が並存することも居心地の悪いものである。
このようなわけで、自分が理解できない「非条件付確率の解答」の不備を指摘して世の中を啓蒙してやろうする数学者がいても不思議ではない。 (あくまでも私の想像である)
また、ホストが開ける扉にくせがあると非条件付確率の解答と特定事象による条件付確率あるいは事後確率の解答で異なる確率値になるが、同一の問題に複数の確率値が並存することも居心地の悪いものである。
このようなわけで、自分が理解できない「非条件付確率の解答」の不備を指摘して世の中を啓蒙してやろうする数学者がいても不思議ではない。 (あくまでも私の想像である)
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). はこの格好の事例といえるかも知れない。
彼らの論文に対する Marilyn vos Savant からの批判に対して書かれた Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991c). を読むと、 他の統計数学者から 非条件付確率の解答 を受け入れないことを批判されてもなお、 彼らが Marilyn vos Savant の問題設定が誤りであると信じている様がわかる。
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., and Doviak, M. J. (2010), を読むと、2010年になってもまだ、この考えから抜けきれていないことがわかる。
※ Wikipedia(英語版) の "Monty Hall problem" の記事(20:04, 18 December 2012 版)の"A second controversy" の項に、 非条件付確率の解答と特定事象による条件付確率あるいは事後確率の解答が一致する条件である標準仮定を仮定することが自然であることを、 彼ら(彼?)が2011 年に受け入れたらしいことが書かれている。 Rosenhouse, Jason.(2009). にも類似の記述がある。
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., and Doviak, M. J. (2010), を読むと、2010年になってもまだ、この考えから抜けきれていないことがわかる。
※ Wikipedia(英語版) の "Monty Hall problem" の記事(20:04, 18 December 2012 版)の"A second controversy" の項に、 非条件付確率の解答と特定事象による条件付確率あるいは事後確率の解答が一致する条件である標準仮定を仮定することが自然であることを、 彼ら(彼?)が2011 年に受け入れたらしいことが書かれている。 Rosenhouse, Jason.(2009). にも類似の記述がある。
◇ 間違えて恥をかいた。
モンティ・ホール問題を統計数学者が解けなくても恥ではないことが当時まだ知られていなかったため、答えを間違えた数学の先生たちは恥ずかしさを感じるばかりであった。そして自分の名誉回復のため、標準仮定だけの議論では不十分だということを述べたり、Marilyn vos Savant の解き方では答えが得られない変形問題をひねり出したりした。 (あくまでも私の想像である)
◇ 自尊心が傷ついた。
統計数学の専門家を自認しているような先生や学生がモンティ・ホール問題を間違えると、人前で恥をかかなかったとしても自尊心が傷つくだろう。 そうした人たちが専門家ならではの目で問題を分析して自尊心を取り戻したかったのかもしれない。(あくまでも私の想像である)
ワーディングを議論した数学者たちが後世に残した成果
ワーディングの議論の内容そのものは、Diaconis のような大物が数語で片付けてしまうような価値の低い問題である。しかし、後世に残した成果が皆無というわけではない。
◇ 標準仮定の重要性の認知を広めた
少なくとも統計数学界では、標準仮定のあいまいな問題文を作ったり、標準仮定を明記せずに論じるような数学者が減っただろう。
あるいはモンティ・ホール問題を友人に説明していたら、横からワーディングの議論の知識のある奴にツッコミを入れられたようなときに、「そんなことは先刻承知、Wkipediaに書いてあるよ」と反論できる。
あるいはモンティ・ホール問題を友人に説明していたら、横からワーディングの議論の知識のある奴にツッコミを入れられたようなときに、「そんなことは先刻承知、Wkipediaに書いてあるよ」と反論できる。
数学の問題としてのとらえ方が複数あることの認知を広めた。
非条件付確率の問題設定は誤りだとする数学者と、誤りではないとする数学者の論争を通して、条件付確率を求める特定事象による条件付確率あるいは事後確率の問題設定以外の問題設定も成立することの認知を広めた。
確率に関する問題で、結果に影響する仮定を無意識にすることがあることを知らしめた。
このような心構えが重要になるような重大な人生の局面に巻き込まれる人もいるだろう。
3囚人問題ではワーディングが論じられない理由
3囚人問題では、ワーディングが議論された形跡がまったく無い。囚人Aの方から看守に掛け合って問題がスタートしているのでルールの曖昧さが少ないことが理由だろう。
Wikipedia(英語版)でのワーディングの議論の扱い
Wikipedia(英語版)の"Monty Hall problem"の記事(2012年3月19日 20:49版)でワーディングの議論を紹介している"Criticism of the simple solutions"の項目の内容の一部をご紹介する。
- ◇モンティ・ホール問題を数学の問題としてとらえる方法に次の2通りがあるとしている。
1.What is the probability of Bryan winning the car if he will abandon his initial pick? 2.What is the probability of the car being behind the door 2 (注:ブライアンというのは架空の挑戦者の名前である)
この2つのとらえ方は私が言う、非条件付確率の問題設定と特定事象による条件付確率あるいは事後確率の問題設定に対応する。
- ◇ホストの行動パターンによっては、これらの2つのとらえ方で確率の計算結果が異なることを述べている。
- ◇非条件付確率の問題設定を誤りだとするMorgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991). の意見と、どちらも正しいとするBehrends (2008)の意見を併記している。
エンターテインメントの素材としてのモンティ・ホール問題
テレビの教育番組や教養娯楽番組に登場したモンティ・ホール問題
| 番組 | 内容 |
|---|---|
| 2010年1月3日放送のフジテレビ 「平成教育委員会」 |
正月番組らしく三つのお年玉袋を使っている。 実験はしていない。 |
| 2011年07月06日放送のNHK 「ためしてガッテン」 (「数字トリック見破り術」) | 番組では、図表で解説したり、中学生参加で実験したりしている。ネットで調べると四国の中学校らしい。ホームページでも解説している。 |
| 2011年7月8日放送のNHK 「23:55」 |
紙コップ四つを扉に見立て、キャンディを賞品に見立てて爆笑問題の田中に紙コップを選ばせている。 ためしてガッテンと同時期にもかかわらず、説明の仕方が異なることにビックリ。 |
|
BBCのWebサイトの "NEWS MAGAZINE" の "Stick or switch? Probability and the Monty Hall problem"というページの動画 2013/09/12 という日付が付いている |
数学者 Marcus du Sautoy が紙コップとその中に入るヤギ、豚、牛のフィギュア、およびミニカーを使って実験している。 |
テレビドラマ、小説、コミックなどに登場したモンティ・ホール問題
| 番組 | 内容 |
|---|---|
| 2003年頃のフジテレビ知的深夜バラエティ番組 「数と共に去りぬ」 | 時限爆弾の3本の配線を扉に見立てている。 |
| 2012/2/29放送の日テレ 「数学♥女子学園」 第8話 |
公式ホームページによると 「消費期限切れメンタイコパンをさゆり(道重さゆみ)が、捨ててしまったことが発端となり、・・・」 Wikipedia(フランス語版) の "Problème de Monty Hall" の記事でも紹介 |
|
「嘘喰い」 第302話 「直感と論理」 ネットで検索して出てくる記事は2012年10月ごろの記事が多い。 |
Googleの画像検索で船の船腹に無数の扉がある情景を見ることができた。 |
|
「長い廊下がある家」(有栖川有栖、光文社文庫)の中の「ロジカル・デスゲーム」 2013/07/20 初版1刷 |
ネット上の紹介文によると、探偵が別の男に命を懸けたゲームを強いられ、グラスが3つあり、・・・といった内容らしい。 |
映画やTVドラマ、およびコント仕立てのクイズに出てくる モンティ・ホール 問題は、説明不足のため「標準仮定」を読み取ることができなかったり、もはや モンティ・ホール 問題とは言えないような問題設定になっていたりする。
以下、似非モンティ・ホール問題の例を類型別にあげる。
以下、似非モンティ・ホール問題の例を類型別にあげる。
「問題すり替わり型」似非モンティ・ホール問題の例
ホストの行動がくずれて標準仮定が成立しないことが明白になってしまったケースがある。
2003年頃のフジテレビ知的深夜バラエティ番組[「数と共に去りぬ」の似非 モンティ・ホール 問題
ある人のブログで紹介されている内容を要約する。
犯人が仕掛けた時限爆弾に赤、黄、青の3本の線があり、特定の1本を切ると爆弾が停止し、他の線を切ると爆発する。
爆弾処理者が「いちかばちか青を切る」と述べた。
そこへ犯人から「黄色を切ると爆発する」と電話で知らせて来た。
居合わせた数学者がモンティ・ホール問題を参考にして赤を切るべしと述べた。
爆弾処理者が青を切ろうとしていることを犯人が知らずに、黄色は爆発だと知らせて来たとするなら、青を切っても赤を切っても確率は等しくなってしまう。
インターネットで見かけた自己流モンティー・ホール問題
ある人のブログに、その人が作った自己流問題文がモンティ・ホール問題として紹介されていたが、明白に標準仮定が成立しない似非モンティ・ホール問題であった。問題の箇所を要約すると次のようになる。
参加者が選んだ「B」以外の箱に司会者がうっかりぶつかって蓋がずれた。
その隙間からハズレの賞品が見えることに参加者が気付いた。
このような問題文では挑戦者が選んだ箱が当たりである確率が 1/2 になる。
3囚人問題でも、囚人Bの処刑日の書かれた予定表を囚人Aが偶然に見たという設定にすれば、同じ理屈になる。
「ホストの行動ルールあいまい型」似非モンティ・ホール問題の例
ホストの行動ルールの記述が貧弱なため、標準仮定が成立するともしないとも判断できない似非モンティ・ホール問題である。
①"Ask Marilyn"の問題文を雑にコピーしたケース
小説に載った似非(かも知れない)モンティ・ホール問題
2003年出版のMark Haddon の小説"the curious incident of the dog in the night-time"で"Aks Marilyn"の問題を題材にしていて、そこに出てくる問題文は "Ask Marilyn"の問題文をコピーしたものであるが、
惜しむらくは、"Ask Marilyn"の問題文の中の、
"the host. who knows what's behinde the doors, opens another door, say #3, which has a goat."
というくだりが
"Now Monty Hall opens a different door, say #3 to reveal a goat."
という曖昧な別の文章になってしまい、標準仮定の中の「ホストはハズレの扉しか開けない」という条件が読み取りにくくなっている。ホストが開けた扉がたまたまヤギだったと解釈したならば、switch して賞品を得る確率は 1/2 となる。
②数学教室での実演形式の問題文で説明不足のケース
米国のTVドラマ NUMB3RS に出て来た似非モンティ・ホール問題
U-Tubeで見たところ、問題のシーンは次のようである。
数学教師がモンティ・ホール問題を題材に講義を行っている。
扉に見立てた3枚のボードがある。
教師が挑戦者を募ると、女学生が挙手して選ばれ、女学生が真ん中の扉を選択する。
教師が「あなたが選ばなかった扉を開ける」と言いながら扉3に見立てたボートを裏返すとヤギの絵が出てくる。
このように挑戦者が選んでから教師がホストの行動を説明しているので、ルールを示しているのか、エピソードを示しているのか区別がつかなくなってしまい、「③ホストは必ず残りの扉を一枚開ける」という仮定が保証されなくなってしまっている。
モンティ・ホール問題の変形問題の「地獄から来たモンティ」だと解釈したならば、switch して賞品を得る確率は 0 になり、「天使モンティ」だと解釈したならば、1になる。
2008年公開アメリカ映画「ラスベガスをぶっつぶせ」( 原題 "21" )の中の似非 モンティ・ホール 問題
「ラスベガスをぶっつぶせ」という映画に、大学教授が モンティ・ホール 問題を授業するシーンがある。
U-Tubeで見たところ、問題のシーンは次のようである。
U-Tubeで見たところ、問題のシーンは次のようである。
縦にスライドする黒板が3組横並びになっているのを、3枚の扉に見立てる。
一つに新車があり、他の二つにヤギが居て、挑戦者が新車の扉を当てれば新車が手に入ると、教師が述べる。
挑戦者役を募ったところ、主人公が選ばれて主人公が扉1(黒板1)を選ぶ。
教師が「ホストは当たり扉を知っている。あなた(主人公)が選ばなかった扉を開ける」と言いながら
扉3に見立てた黒板3のスライド可能部分をスライドさせる。
黒板3のスライド可能部分の下から出て来た面には何も書いてなかった。
扉3はヤギだと教師が述べてから、教師が主人公に扉2にswitchするか否か、問う。
主人公が扉2に switch すると答えると、教師ががっかりした表情をしながら、何故 switch するのか主人公に問う。
主人公が "variable change"(数学用語にない) を使って解いたと言う。
"variable change"という言葉を聞いた教師が、「こいつは出来る」という表情をする。
上記の NUMB3RS のシーンと同様、「地獄から来たモンティ」である可能性が高くなってしまっている。
"variable change"を、秋山仁先生が数学用語の「変数変換」と訳したことでも話題になっている。
NHKの深夜番組「23:55」でのモンティ・ホール問題
NHKの 「23:55」 の爆笑問題のコーナーでモンティ・ホール問題が取り上げられたことがある。
そのときの内容はこちら → "【ちょっと寄り道】 NHKの深夜番組「23:55」でのモンティ・ホール問題"
2017年の再放送を見たときに、改めてよく考えてみたところ、そもそもモンティ・ホール問題になっていないことに気づいた。 「数学教室での実演形式の問題文で説明不足のケース」 に該当するからである。
2017年に再放送を見たとき、田中が最終的に選んだコップが空だとわかっときにほんの一瞬だけ眉をしかめていたことに気づいた。
そのときの内容はこちら → "【ちょっと寄り道】 NHKの深夜番組「23:55」でのモンティ・ホール問題"
2017年の再放送を見たときに、改めてよく考えてみたところ、そもそもモンティ・ホール問題になっていないことに気づいた。 「数学教室での実演形式の問題文で説明不足のケース」 に該当するからである。
2017年に再放送を見たとき、田中が最終的に選んだコップが空だとわかっときにほんの一瞬だけ眉をしかめていたことに気づいた。
「等確率開扉の仮定」を守りきれない似非かも知れないモンティ・ホール問題
自分がホスト役になって、カードや紙コップを扉に見立ててモンティ・ホール問題を実演しようとすると、等確率開扉の仮定を忠実に守ることが困難である。
例えば、ホスト役の自分に手前のカードばかりをめくる癖があると、相手が switch して賞品を得る確率は 2/3 ではなく、1 や 1 / 2 になってしまう。
標準仮定を前提とした立場の人にとって、こうしたモンティ・ホール問題は「似非モンティ・ホール」問題に見える。(私も以前はそうだった)
しかし、U-Tube などで実際の Monty Hall のゲームを観ると、等確率開扉の仮定の妥当性を云々できるような状況でないことがわかる。
Monty Hall は同じゲームを繰り返して行っていないようなので、ホストの行動パターンに関する統計データは得られそうにもない。
モンティ・ホール問題を特定事象による条件付確率あるいは事後確率の問題設定と捉え、かつ、自分を含む誰かが統計データを取っているような状況でもなければ、自分がホスト役になって、カードや紙コップを扉に見立ててモンティ・ホール問題を実演するときに、等確率開扉の仮定が保証できないことに後ろめたさを感じる必要はなさそうである。
例えば、ホスト役の自分に手前のカードばかりをめくる癖があると、相手が switch して賞品を得る確率は 2/3 ではなく、1 や 1 / 2 になってしまう。
標準仮定を前提とした立場の人にとって、こうしたモンティ・ホール問題は「似非モンティ・ホール」問題に見える。(私も以前はそうだった)
しかし、U-Tube などで実際の Monty Hall のゲームを観ると、等確率開扉の仮定の妥当性を云々できるような状況でないことがわかる。
Monty Hall は同じゲームを繰り返して行っていないようなので、ホストの行動パターンに関する統計データは得られそうにもない。
モンティ・ホール問題を特定事象による条件付確率あるいは事後確率の問題設定と捉え、かつ、自分を含む誰かが統計データを取っているような状況でもなければ、自分がホスト役になって、カードや紙コップを扉に見立ててモンティ・ホール問題を実演するときに、等確率開扉の仮定が保証できないことに後ろめたさを感じる必要はなさそうである。
「似非モンティ・ホール問題」 というより 「新種のモンティ・ホール問題」 と呼ぶべき例
一見するとモンティ・ホール問題のようであるが、詳細に調べると 特定事象による条件付確率あるいは事後確率の問題設定 をとることができなかったり、 標本空間が別物であったりして、 厳密にはモンティ・ホール問題でないものがある。
①扉が区別できない問題文にしてしまったケース
平成教育委員会でのお年玉袋を使ったモンティ・ホール 問題もどき
2010年1月3日の平成教育委員会で、お年玉のポチ袋3つを使った問題が出された。
ある人のブログにこのときの出題内容が詳しく書かれていて、それによると次のような出題内容であったらしい。
ある人のブログにこのときの出題内容が詳しく書かれていて、それによると次のような出題内容であったらしい。
ポチ袋が3つあり、その中の一つにお年玉が入っている。
子供役がポチ袋の一つを取る。
親役のたけし先生が残りの二つをとり、片方の中身を確認してから空だと言う。
Yahoo! 知恵袋などのQAを見ても大体似たような展開である。
実はこのような問題形式は「対戦型モンティ・ホール問題」とよばれるもので、いわゆる「モンティ・ホール問題」すなわち「標準型モンティ・ホール問題」とは、厳密には区別されるものである。
対戦型形式と標準型形式
実際、番組の中では「モンティ・ホール問題」という言葉はまったく使われていなかったらしい。
補足1
「対戦型モンティ・ホール問題」で数学的なとらえ方が 不特定事象による条件付確率あるいは事後確率の問題設定 、もしくは 非条件付確率の問題設定 に限定されることを承知の上でモンティ・ホール問題の一種に数える人もいるかも知れない。
「対戦型モンティ・ホール問題」でも 、たけし先生が開ける袋が最初に見た袋か 2番目に見た袋かを区別できるような状況であれば、 特定事象による条件付確率あるいは事後確率の問題設定 をとることができるので、まったくモンティ・ホール問題からかけ離れているわけでもない。
「対戦型モンティ・ホール問題」でも 、たけし先生が開ける袋が最初に見た袋か 2番目に見た袋かを区別できるような状況であれば、 特定事象による条件付確率あるいは事後確率の問題設定 をとることができるので、まったくモンティ・ホール問題からかけ離れているわけでもない。
補足2
2010年1月3日の平成教育委員会の出題内容には次のような疑問点もある。
「最初に確認した袋に入っていたら別の袋を開けて、最初に確認した袋に入っていなかったらその袋を開ける」 というような手順の場合、
たけし先生が最初に見た袋を開けた場合に残りの袋が当たりである確率は 1/2 になり、
たけし先生が最初に見た袋を開けなかった場合にその袋が当たりである確率は 1 になる。 (2013/07/29 にこの文を訂正)
最初に見た袋がハズレの場合も残りの袋を開けて、片方当りならハズレの方を開けて、両方ハズレだったらどちらかを開けるといった手順なら、どんな場合にも残りの袋が当たりである確率は 2/3 になるかと思いきや、こんどは、たけし先生の表情からたけし先生が当りの袋を持っているかどうか判別できそうである。
たけし先生が手に持った2つの袋の中を同時に見るしかない。
「最初に確認した袋に入っていたら別の袋を開けて、最初に確認した袋に入っていなかったらその袋を開ける」 というような手順の場合、
たけし先生が最初に見た袋を開けた場合に残りの袋が当たりである確率は 1/2 になり、
たけし先生が最初に見た袋を開けなかった場合にその袋が当たりである確率は 1 になる。 (2013/07/29 にこの文を訂正)
最初に見た袋がハズレの場合も残りの袋を開けて、片方当りならハズレの方を開けて、両方ハズレだったらどちらかを開けるといった手順なら、どんな場合にも残りの袋が当たりである確率は 2/3 になるかと思いきや、こんどは、たけし先生の表情からたけし先生が当りの袋を持っているかどうか判別できそうである。
たけし先生が手に持った2つの袋の中を同時に見るしかない。
②扉の中のハズレ賞品を区別できると解釈したケース
モンティ・ホール問題の問題文には、Steve Selvin が作った世界最初の問題文のようにハズレ賞品が無いものと、 Craig F. Whitaker さんが Marilyn vos Savant に出題した問題文のようにハズレ賞品のヤギがあるものがある。
後者の場合、2頭のヤギを区別してヤギに着目して問題を解く事ができる。
例:
Wikipedia(英語版) の "Monty Hall problem" の記事から一時削除されていたが、 2012年11月19日 16:45の版で復活した説明図.。 挑戦者の顔と手のイラストで、挑戦者が選んだ賞品を示している。
しかし、以下に上げる理由から、ハズレ賞品を区別して問題を解いたら、厳密には 「モンティ・ホール問題」 と良く似た 「ハズレ賞品付きモンティ・ホール問題」 を解いたと言うべきである。
理由1
後者の場合、2頭のヤギを区別してヤギに着目して問題を解く事ができる。
例:
Wikipedia(英語版) の "Monty Hall problem" の記事から一時削除されていたが、 2012年11月19日 16:45の版で復活した説明図.。 挑戦者の顔と手のイラストで、挑戦者が選んだ賞品を示している。
しかし、以下に上げる理由から、ハズレ賞品を区別して問題を解いたら、厳密には 「モンティ・ホール問題」 と良く似た 「ハズレ賞品付きモンティ・ホール問題」 を解いたと言うべきである。
理由1
Steve Selvin が作った元祖モンティ・ホール問題ではハズレの箱は空である。
理由2
ハズレ賞品を区別して扉を区別しない解き方と、扉を区別してハズレ賞品を区別しない解き方が同じ問題を解いていると言えるのは、問題の捉え方を 非条件付確率の問題設定 に限定し、さらに解き方も挑戦者の最初の選択を特定しない方法に限定した場合に限られる。
デマを含んだ解説文や書籍を読んだ人たちがネット上でそのデマを広めているところを見ることがある。
そのようなデマをいくつか上げる。
そのようなデマをいくつか上げる。
モンティ・ホール問題の由来に関するデマ
モンティ・ホール問題は Monty Hall のゲームそのものに関する問題だ
「モンティ」という固有名詞がやたらと出てくる解説文を読んで、モンティ・ホール問題は Monty Hall のゲームそのものに関する問題だと勘違いしている人を、インターネットでよく見かける。
モンティ・ホール問題のゲームと Monty Hall が実際に行ったゲームとの類似性は薄いので、正しくは、「Monty Hall のゲーム番組の中のゲームをヒントに、モンティ・ホール問題が生み出された」と言うべきである。
モンティ・ホール問題のゲームと Monty Hall が実際に行ったゲームとの類似性は薄いので、正しくは、「Monty Hall のゲーム番組の中のゲームをヒントに、モンティ・ホール問題が生み出された」と言うべきである。
- ※Steve Selvin への返事の中で、挑戦者に switch の機会を与えない場合があることを Monty Hall が述べているので、Monty Hall が行ったゲームはモンティ・ホール問題のゲームと重要な点で食い違っている。Monty Hall(1975).
- ※U-Tube などで Monty Hall のゲーム番組の映像を調べても、モンティ・ホール問題のゲームに似たゲームを Monty Hall が行っているシーンを見ることは稀で、その稀なゲームについても、ゲームの進め方がモンティ・ホール問題のゲームと異なっている。
モンティ・ホール問題はクイズミリオネアのようなクイズ番組に関する問題だ
モンティ・ホール問題を紹介している書籍の邦訳で、"game show" を「クイズ番組」と訳しているものがある。
それを読んでクイズミリオネアのような番組に関する問題だと勘違いしている人を、インターネットでよく見かける。
さらに進んでバラエティ番組だと勘違いしている人もいる。
モンティ・ホール問題ができた1975年のアメリカのテレビ番組でなく、自分が日頃目にしているテレビ番組の中に類似のものを探した結果だろう。
それを読んでクイズミリオネアのような番組に関する問題だと勘違いしている人を、インターネットでよく見かける。
さらに進んでバラエティ番組だと勘違いしている人もいる。
モンティ・ホール問題ができた1975年のアメリカのテレビ番組でなく、自分が日頃目にしているテレビ番組の中に類似のものを探した結果だろう。
モンティ・ホール問題はクイズ番組でモンティ・ホールという名の人が出した問題だ
伝言ゲームのようにデマの内容が変容している。
ワーディングの議論に関するデマ
問題文があいまいなので、Marilyn vos Savant に反論した人が間違っているとは言い切れない
"Ask Marilyn"の問題文は曖昧なため、標準仮定が成立するとは限らないので、Marilyn vos Savant に反論した人々は間違っているとは言い切れないと書いている解説文があった。(2010年8月現在)
実際には、問題文の曖昧さと確率の錯覚との間に因果関係がほとんど無いことが心理学的研究で明らかになっている。
【補足】
もしかしたら、この説を述べた人は、Marilyn vos Savant に反論した人々の考え方が間違っているか否かではなく、答えの数値だけに着目しているのかも知れない。
実際には、問題文の曖昧さと確率の錯覚との間に因果関係がほとんど無いことが心理学的研究で明らかになっている。
【補足】
もしかしたら、この説を述べた人は、Marilyn vos Savant に反論した人々の考え方が間違っているか否かではなく、答えの数値だけに着目しているのかも知れない。
問題文があいまいなので、残った扉が当りである確率がどちらも 1 / 2 だと考えてもおかしくない
確率の手掛かりが無い場合に、おこりうるケースすべてに同じ確率を割り振るのは日常の確率概念の世界の話であり、数学パズルであるモンティ・ホール問題に当てはめようとするのは、すじ違いである。
日常の確率概念では理解できない種類の数学の問題から逃れようとして、 このデマがひねり出されたのだろう。
日常の確率概念では理解できない種類の数学の問題から逃れようとして、 このデマがひねり出されたのだろう。
確率が 1/2 だと答えた人はホストが当たりの扉を開けることもあると考えたのだ
実際は、確率が 1/2 だと錯覚した人で、標準仮定を読み取らなかった人は少ない。
問題文が曖昧だから確率が 1/2 だと錯覚したのだと言い訳する人の少なさはインターネット上のQAサイトやブログを見てもわかる。
このデマを流す人は 「問題文があいまいなので、Marilyn vos Savant に反論した人が間違っているとは言い切れない」 という説を読んで勘違いしたのだろう。
あるいは 「ホストが当たりの扉を開けることもあれば確率が 1/2 になる」 と知ったために勘違いしたのかも知れない。
【補足】
「ホストが当たり扉を開けることもある」という条件の下に数学的な手順で確率 1/2 と答えた人は多くない。ホストがハズレ扉を開けることもあるという条件を数学的に考慮しつつ確率 1/2 と答えられる人は、条件付確率の計算に慣れているはずである。ホストが当たり扉を開けてしまうケースも考慮しなければならないからだ。そのようなレベルの人なら、「ホストが当たり扉を開けることもある」という条件以外の条件にも気付くだろうから、単純に確率が 1/2 だと答えたりしないだろう。
問題文が曖昧だから確率が 1/2 だと錯覚したのだと言い訳する人の少なさはインターネット上のQAサイトやブログを見てもわかる。
このデマを流す人は 「問題文があいまいなので、Marilyn vos Savant に反論した人が間違っているとは言い切れない」 という説を読んで勘違いしたのだろう。
あるいは 「ホストが当たりの扉を開けることもあれば確率が 1/2 になる」 と知ったために勘違いしたのかも知れない。
【補足】
「ホストが当たり扉を開けることもある」という条件の下に数学的な手順で確率 1/2 と答えた人は多くない。ホストがハズレ扉を開けることもあるという条件を数学的に考慮しつつ確率 1/2 と答えられる人は、条件付確率の計算に慣れているはずである。ホストが当たり扉を開けてしまうケースも考慮しなければならないからだ。そのようなレベルの人なら、「ホストが当たり扉を開けることもある」という条件以外の条件にも気付くだろうから、単純に確率が 1/2 だと答えたりしないだろう。
挑戦者がホストの行動ルールを知らされていることが重要だ
挑戦者の目から見た確率を求めることがモンティ・ホール問題の課題だと解釈して、標準仮定を挑戦者が知らなければ標準仮定が成立していないに等しいと説明している解説文があった。(2010年8月現在)
以下、こういった考え方がデマであるか、デマでないにしても少数派であることの根拠を上げる。
以下、こういった考え方がデマであるか、デマでないにしても少数派であることの根拠を上げる。
- 挑戦者になったつもりで解くことを求めている問題文もあるが、 Steve Selvin が作った世界最初の問題文のように、 第三者の目で解く事を求めている問題文もある。
- モンティ・ホール問題を世界的に有名にした Craig F. Whitaker の問題文のように、挑戦者になったつもりになることを求めている問題文もあるが、そのような問題文を読んだとしても、挑戦者がホストの行動ルールを知らない可能性を考慮する人は少ない。
- そもそもホストの行動ルールを知らない挑戦者になったつもりで確率を考えよと言われたら、答えは無いと答えるか、もはや数学パズルでないと答えるしかない。
数学的な問題としてのとらえ方に関するデマ
モンティ・ホール問題はベイズ理論の例題だ
モンティ・ホール問題を 特定事象による条件付確率あるいは事後確率の問題設定 でとらえたとしても、問題を解くためにベイズの定理もベイズ推定の公式も不可欠でないので、正しくは 「ベイズ理論の公式の練習問題にモンティ・ホール問題が使える」 と言うべきである。
ホストがハズレ扉を開けるときに扉を選り好みする癖があれば、switch して賞品を得る確率が 2/3 にはならない。
このようなことが言えるのは、モンティ・ホール問題を条件付確率や事後確率の問題として捉えた場合に限定されるので、そのことを言い添えなければデマになる。 あるいはデマと言えないまでも、重大な言葉足らずだと言える。
そもそも、ホストの癖に関する統計データを誰も取っていなければ、ホストにどんな癖があろうとも、お釈迦さまでない人間さまには「ホストに癖があったら 2/3 でない」と一般法則を唱えることしかできない。このことから、モンティ・ホール問題を条件付確率や事後確率の問題として捉えるのは、数学的に高尚なように見えて、実は初心者の考え方だということがわかる。
数年前(2010年)に自力で条件対確率を計算して、尤度 (当り扉ごとのホストが開ける扉の確率) の重要性に気付いた自分を自慢していた当時の私も、今の私から見れば初心者に過ぎない。
そもそも、ホストの癖に関する統計データを誰も取っていなければ、ホストにどんな癖があろうとも、お釈迦さまでない人間さまには「ホストに癖があったら 2/3 でない」と一般法則を唱えることしかできない。このことから、モンティ・ホール問題を条件付確率や事後確率の問題として捉えるのは、数学的に高尚なように見えて、実は初心者の考え方だということがわかる。
数年前(2010年)に自力で条件対確率を計算して、尤度 (当り扉ごとのホストが開ける扉の確率) の重要性に気付いた自分を自慢していた当時の私も、今の私から見れば初心者に過ぎない。
ホストがハズレ扉を開けるときの癖を考慮していない Marilyn vos Savant の答えは間違いだ
挑戦者が当たり扉1を選んだときに、ホストがハズレ扉3を開ける確率が 1/2 でないケースを考慮していないからMarilyn vos Savantの答えは間違いだとする説がある。しかし、Marllyn vos Savant が解いた問題設定にはホストが扉3を開ける確率に影響を受ける要素が含まれていないので、完全に的外れな意見である。
モンティ・ホール問題を 条件付確率や事後確率の問題 として捉えないのは間違いだ
こういった考えが誤りであることは次のようにして分かる。
このような考え方は、モンティ・ホール問題の中のゲームを現実のものとしてとらえていて、ホストの行動のくせも加味した詳細な分析をしなければならないとしている。
この考え方が正しいなら、ホストの行動のくせについて、 当り扉の配置とホストが開ける扉の関係だけでなく、ホストは前回どの扉を開けたか、ホストは挑戦者のどちら側に立っているか、・・・など無限に考慮すべき項目が出てくる。
したがって、人間はモンティ・ホール問題を解く事ができなくなる。
同様なことは人間が遭遇するすべての確率の問題に言えることであるから、人間は確率について何も言えなくなってしまう。
こうなりたくなければ、 「モンティ・ホール問題を 非条件付確率の問題 として捉える考え方もあり」 としなければならない。
「モンティ・ホール問題を 条件付確率や事後確率の問題 として捉えないのは間違いだ」 と主張する人は、 「非条件付確率の問題設定」 による解答 (Wikipedia(英語版)の"Monty Hall problem"の記事で言う"symple solutions") を理解できないか、理解できても受け入れられないのだろう。
こうした考え方の背景には、 「証拠事象の現象が発生するたびに標本空間を自動的に切り替える」 という確率判断のヒューリスティクの性質が関係しているの化も知れない。
ヒューリスティクのこうした性質のため、標本空間の切替を伴わない解答を理解できない人や、理解しても受け入れることのできない人が出てくるのだろう。
あるいは、 「第ニ部 モンティ・ホール問題と3囚人問題の認知心理学的検討」 の 「確率の錯覚のメカニズムに関する私の仮説」 で述べた 「客観確率幻想」 が関係しているのかも知れない。
扉という客体自体に確率が宿っているという幻想のため、数学的な問題のとらえ方によって確率が異なるという考えが受け入れられないのだろう。
このような考え方は、モンティ・ホール問題の中のゲームを現実のものとしてとらえていて、ホストの行動のくせも加味した詳細な分析をしなければならないとしている。
この考え方が正しいなら、ホストの行動のくせについて、 当り扉の配置とホストが開ける扉の関係だけでなく、ホストは前回どの扉を開けたか、ホストは挑戦者のどちら側に立っているか、・・・など無限に考慮すべき項目が出てくる。
したがって、人間はモンティ・ホール問題を解く事ができなくなる。
同様なことは人間が遭遇するすべての確率の問題に言えることであるから、人間は確率について何も言えなくなってしまう。
こうなりたくなければ、 「モンティ・ホール問題を 非条件付確率の問題 として捉える考え方もあり」 としなければならない。
「モンティ・ホール問題を 条件付確率や事後確率の問題 として捉えないのは間違いだ」 と主張する人は、 「非条件付確率の問題設定」 による解答 (Wikipedia(英語版)の"Monty Hall problem"の記事で言う"symple solutions") を理解できないか、理解できても受け入れられないのだろう。
こうした考え方の背景には、 「証拠事象の現象が発生するたびに標本空間を自動的に切り替える」 という確率判断のヒューリスティクの性質が関係しているの化も知れない。
ヒューリスティクのこうした性質のため、標本空間の切替を伴わない解答を理解できない人や、理解しても受け入れることのできない人が出てくるのだろう。
あるいは、 「第ニ部 モンティ・ホール問題と3囚人問題の認知心理学的検討」 の 「確率の錯覚のメカニズムに関する私の仮説」 で述べた 「客観確率幻想」 が関係しているのかも知れない。
扉という客体自体に確率が宿っているという幻想のため、数学的な問題のとらえ方によって確率が異なるという考えが受け入れられないのだろう。
確率解釈論に関するデマ
モンティ・ホール問題の確率は「主観確率」だから不思議なのだ
この説を唱える人は、モンティ・ホール問題や3囚人問題の答えを頭で理解しても、心で納得できない理由を、確率解釈論に求めているのだろう。しかし次のように、この説がデマである理由を上げることができる。
デマである理由1:
デマである理由1:
既に発生している現象に関する確率は「主観確率」だと説明する人もいる。 たとえばある数学教師はブログで、『ゲーム開始時点で当たり扉が「物理的に」決まっているので、当たり扉の確率は「主観確率」でしか有り得ない』と説明していた。
このようにゲーム開始時点の確率も「主観確率」だとすると、「どうして最初の確率が 1/3 なのか納得できない」という声が湧き起こるはずであるが、そのような声を聴いたことがない。
このようにゲーム開始時点の確率も「主観確率」だとすると、「どうして最初の確率が 1/3 なのか納得できない」という声が湧き起こるはずであるが、そのような声を聴いたことがない。
デマである理由2:
事後確率やベイズ確率のことを指して「主観確率」だと呼ぶ人もいる。 一方、モンティ・ホール問題は、一般的には非条件付確率の問題設定で解くことが多い。 この場合、求めた確率は事後確率でもベイズ確率でもないので「主観確率」でないことになるが、心で納得しづらいことに変りはない。.
デマである理由3:
事後確率としての「主観確率」の代表選手はガン検診を受けた後にガンに掛かっている確率である。 しかしこの種の確率に対して「納得できない」という言葉は余り聴かれない。自分たちの生死につながる問題にもかかわらずである。
モンティ・ホール 問題の確率は「主観的確率」だ
「モンティ・ホール問題は「主観確率」の例題のひとつだ」 と解説している資料を読んだかして 「モンティ・ホール 問題の確率は「主観的確率」 だと勘違いしている人をインターネットで見かけることがあるが、 哲学 (確率認識論) 用語の 「主観確率」 と 日常語の 「主観的確率」 は全く別物である。
「主観確率」 と 「主観的確率」 を英語で言うと、それぞれ "subjective probability"、 "personal probability" となるので、混同しづらい。
「主観確率」 と 「主観的確率」 を英語で言うと、それぞれ "subjective probability"、 "personal probability" となるので、混同しづらい。
3囚人問題は人気が薄いのでインターネットで調べても Wikipedia(日本語版)の 「3囚人問題」の記事以上の情報に当ることは稀である。 それでも時間を掛ければ多少は見つかるものである。
3囚人問題の問題文のいろいろ
Mosteller, Frederick (1987).に載っている 3囚人問題は、何と!、ロシアンルーレット型の 3囚人問題である。
通常の 3囚人問題との違いは次の通り。
通常の 3囚人問題との違いは次の通り。
通常の 3囚人問題との違いは次の通り。
- 処刑される囚人がいない代わりに、釈放される囚人が二人いる。
- 質問する囚人は看守と友達である。
- 主人公の囚人は看守に、自分以外で釈放される一人の名を聞こうかと思ったが、そうすると釈放される確率が 2/3 から 1/2 に下がるので質問をしない方が良いと思ってしまう。
通常の 3囚人問題との違いは次の通り。
|
|
|
|---|---|
| 恩赦 (一人) | 釈放 (一人) |
| 処刑 (二人) |
|
「3囚人問題」 の別名 「サーベロニ問題」 の謎について
「3囚人問題」 というキーワードで検索すると、「3囚人問題はサーベロニ問題という呼び名で古くから知られていた問題である」 と書いているブログや、 「サーベロニの別荘で行われた学会で激論となったことがこの呼び名の由来だ」 と書いているブログが出てくる。
何やら面白げなので調べて見ると、実際は下記のように面白くも何ともない。
何やら面白げなので調べて見ると、実際は下記のように面白くも何ともない。
「サーベロニ問題」 という名称の由来
北イタリアのコモ湖のベッラージョ岬にロックフェラー財団のベッラージョ・センター(通称 "Villa Serbelloni") がある。
"Villa Serbelloni" はイタリア語で発音すると 「ヴィッラ・セルベッローニ」 であるが、英語で発音すると 「ヴィラ・サーベロニ」 になる。
Wikipedia(英語版) の "Brian Goodwin" (生物学者) の記事によると、このセンターで 1965年から 1968年に掛けての各年に、 "Towards a theoretical Biology" と銘打った理論生物学の学術会議が催されたらしい。
この学術会議には John Maynard Smith も参加している。
そのうちの 1966年の会議が 「難破」 しそうになるほどの激論になったことにちなんで、 John Maynard Smith が "The Serbelloni probrem" という呼称を提案している。Smith, John Maynard (1968).
「難破」 しそうになったのが John Maynard Smith 本人の発表だったのかは、よくわからない。
"Villa Serbelloni" はイタリア語で発音すると 「ヴィッラ・セルベッローニ」 であるが、英語で発音すると 「ヴィラ・サーベロニ」 になる。
Wikipedia(英語版) の "Brian Goodwin" (生物学者) の記事によると、このセンターで 1965年から 1968年に掛けての各年に、 "Towards a theoretical Biology" と銘打った理論生物学の学術会議が催されたらしい。
この学術会議には John Maynard Smith も参加している。
そのうちの 1966年の会議が 「難破」 しそうになるほどの激論になったことにちなんで、 John Maynard Smith が "The Serbelloni probrem" という呼称を提案している。
「難破」 しそうになったのが John Maynard Smith 本人の発表だったのかは、よくわからない。
ロックフェラー財団のベッラージョ・センターの通称名 "Villa Serbelloni" について
(2018年10月に Wikipedia などを再調査して、この段落の内容を次のように訂正しました)
Smith, John Maynard (1968). に出てくる "Villa Serbelloni" という言葉が 「サーベロニの別荘」 と訳されたらしいが、下記の理由で誤訳とおもわれる。
調査した Web ページ
調査結果
このように Villa Serbelloni が広大なので、
"Villa Serbelloni" と呼ばれる建物の意味であれ、
"Villa Serbelloni" と呼ばれるベッラージオセンターの意味であれ、
「別荘」という訳語は適当でない。
"a conference on theoretical biology at the Villa Serbelloni" の翻訳は「ヴィラ・サーベロニでの理論生物学会議」としておいて、脚注でロックフェラー財団のベッラージオセンターのことだと説明する方がよい。
Smith, John Maynard (1968). に出てくる "Villa Serbelloni" という言葉が 「サーベロニの別荘」 と訳されたらしいが、下記の理由で誤訳とおもわれる。
調査した Web ページ
- イタリア語版 Wikipedia の "Bellagio"の記事(20:31, 15 set 2018)
- イタリア語版 Wikipedia の "Villa Serbelloni" の記事(15:41, 13 ott 2018)
- 英語版 Wikipedia の "Rockefeller Foundation" の記事(12:20, 3 October 2018) の"Villa Serbelloni" という章
- comoanditslake.com というサイトの "Villa Serbelloni - Bellagio" というタイトルのページ
- "Villa Serbelloni Gardens | Explore Lake Como" というタイトルのページ
- "Hotel History - Grand Hotel Villa Serbelloni Bellagio" というタイトルのページ
調査結果
- 城の在った場所に Villa が 15世紀に建てられて、18世紀にセルベッローニ家に渡り、20世紀にロックフェラー財団に渡り、ロックフェラー財団のベッラージオセンターになったらしい。
- ベッラージオセンターに含まれない湖岸の街並みも "Villa Serbelloni" の風景として提示されているので、湖岸の建物が密集しているところも Serbelloni の土地だったのかも知れない。
- ベッラージオ岬の丘の頂上付近にある "Villa serbelloni" と呼ばれる建物がベッラージオセンターの最も大きな建物らしい。見晴らしもよいので城があった場所だろう。
- 18世紀に Alessandro Serbelloni が広大な公園のために道やトンネルを整備した。
- ベッラージオセンターは "Villa Serbelloni" と呼ばれることもある。
- ベッラージオセンターの面積は 20万平米 (正方形だと一辺が450m) と広大である。(トランプ大統領の別荘 マー・ア・ラゴ の20倍)
- 公園 (Villa Serbelloni Garden) はロックフェラー財団の所有だがベッラージオ町の管理のもと有料で一般公開されている。
- 湖岸のひと際大きな建物が Grand Hotel Villa Serbelloni という名前のホテルである。
このように Villa Serbelloni が広大なので、
"Villa Serbelloni" と呼ばれる建物の意味であれ、
"Villa Serbelloni" と呼ばれるベッラージオセンターの意味であれ、
「別荘」という訳語は適当でない。
"a conference on theoretical biology at the Villa Serbelloni" の翻訳は「ヴィラ・サーベロニでの理論生物学会議」としておいて、脚注でロックフェラー財団のベッラージオセンターのことだと説明する方がよい。
コモ湖畔の Villa について
「コモ湖 ヴィラ」 でネット検索すると、歴史ある Villa で現在はホテルや博物館になっているがものがいくつか出てくる。
それらの Villa の一つがネスプレッソのコマーシャル (ジョージ・クルーニー出演) のロケ地として使われているのを U-Tube で見ることができる。
それらの Villa の一つがネスプレッソのコマーシャル (ジョージ・クルーニー出演) のロケ地として使われているのを U-Tube で見ることができる。
「3囚人問題はサーベロニ問題という呼び名で古くから知られていた問題である」 という説はデマか
3囚人問題が1950年代 (遅くとも 1959年) から知られているのだから、 この説はデマに他ならない。
しかしインターネットで詳しく検索すると、この呼称だけを使って 3囚人問題を論じている記事も僅かながら出てくるので、 まったくのデマでもない。
「昔は 3囚人問題を 『サーベロニ問題』 という呼び名で覚えた人もいる」 と言い換えれば問題ない。
しかしインターネットで詳しく検索すると、この呼称だけを使って 3囚人問題を論じている記事も僅かながら出てくるので、 まったくのデマでもない。
「昔は 3囚人問題を 『サーベロニ問題』 という呼び名で覚えた人もいる」 と言い換えれば問題ない。
学術会議が 「難破」 しかけたというが、さほどの事件ではなさそうだ
Smith, John Maynard (1968).が 「この問題のせいで学術会議が難破しかけた」 などと面白げに書いたために色々な文献で引用されている。
しかし Wikipedia (日本語版、英語版、フランス語版、ドイツ語版) の 「3囚人問題」 の記事で紹介されていない。(2012年11月02日現在)
インターネットで検索しても肝心の学術会議の様子が出て来ない。
John Maynard Smith本人、もしくは他の誰かの発表の質疑で長い時間をとられたかしたに過ぎないのだろう。
しかし Wikipedia (日本語版、英語版、フランス語版、ドイツ語版) の 「3囚人問題」 の記事で紹介されていない。
インターネットで検索しても肝心の学術会議の様子が出て来ない。
John Maynard Smith本人、もしくは他の誰かの発表の質疑で長い時間をとられたかしたに過ぎないのだろう。
John Maynard Smith は冗談で "The Serbelloni problem"という呼称を提案した・・・と私は思う
彼の提案文は "This should be called the Serbelloni problem since 云々" という強い口調なので、 あくまでもジョークとして書いたに違いない。・・・・・というのが英語力のさほど強くない私の説である。
3囚人問題を 「サーベロニ問題」 や "The Serbelloni problem" の呼称で覚えた人の数
"Serbelloni Problem" でインターネット検索して出てくるのは "Three Prisoners problem" の別名として Smith, John Maynard (1968). を引用する記事が多い。
「サーベロニ問題」 でインターネット検索して出てくるのは、 「3囚人問題は昔サーベロニ問題とよばれていた」 というウンチクが多い。
しかし、よく検索してみると、 3囚人問題を 「サーベロニ問題」 や "The Serbelloni problem" と呼んで 「3囚人問題」 と呼んでいない記事も出てくる。
2012年11月に Google で検索した結果は次のとおり。
重複した検索結果や読解できないページはカウントしていません。
この表から 3囚人問題を 「サーベロニ問題」と呼ぶ記事が英語圏に比べて日本に多いことがわかる。 日本の記事は 2000年代中ごろの記事であることが多く、しかも別の記事の受け売りが多いので、日本では 3囚人問題を 「サーベロニ問題」と覚えた人を起点として 2000年代中ごろからインターネット上で広がっていったのかも知れない。
「サーベロニ問題」 でインターネット検索して出てくるのは、 「3囚人問題は昔サーベロニ問題とよばれていた」 というウンチクが多い。
しかし、よく検索してみると、 3囚人問題を 「サーベロニ問題」 や "The Serbelloni problem" と呼んで 「3囚人問題」 と呼んでいない記事も出てくる。
2012年11月に Google で検索した結果は次のとおり。
| 検索キー |
使っていない件数 |
使っている件数 |
|---|---|---|
|
|
3 | 4 |
| 「サーベロニ問題」 | 10 | 4 |
この表から 3囚人問題を 「サーベロニ問題」と呼ぶ記事が英語圏に比べて日本に多いことがわかる。 日本の記事は 2000年代中ごろの記事であることが多く、しかも別の記事の受け売りが多いので、日本では 3囚人問題を 「サーベロニ問題」と覚えた人を起点として 2000年代中ごろからインターネット上で広がっていったのかも知れない。
2011/10/29 の NHKで錯覚を特集する科学番組を放送していた。司会は小野アナウンサー。番組の最後になんと3囚人問題の研究者、下條信輔が登場して、次のようなことを述べていた。
- 目から視覚野に情報が届くのに 0.1 秒、視覚野から前頭葉に届くのに 0.1秒、計0.2秒も掛かる。
- そのため、動きの早い情景を視覚情報処理するときには未来を予測するような機能が備わっている。
- フラッシュラグ錯覚 (動きの早い物体が実際より先の方にいると勘違いする錯覚) はそうした視覚情報処理の結果である。
- 錯覚をもたらす脳の働きというものは、限られた脳の能力で効率的に外界に適応するために備わった機能である。
下條信輔に「あなたの研究で明らかになった確率判断のヒューリスティクについても同様なことが言えるでしょうか」と質問したら、肯定するに違いない。
モンティ・ホール問題に関する心理学的研究の参考文献
-
Aaron, E. and Spivery, M. (1998).
Frequency vs. probablity formats: Framing the three doors problem. In M. A. Gernsbacher & S. J. Derry(Eds.),
Proceedings of the twentieth annual conference of the Cognitive Science Society (pp. 13-18). Mahwah, NJ: Erlbaum.
-
Brase, G. L., Cosmides, L., & Tooby, J. (1998).
Individuation, counting and statistical inference: The role of frequency and whole-object representations in judgment under uncertainty.
Journal of Experimental Psychology: General, 127, 3–21.
-
Burns, B.D. & Wieths, M. (2004).
The collider principle in causal reasoning: Why the Monty Hall dilemma is so hard.
Journal of experimental Psychology: General, 133, 434-449.
-
De Neys, W. & Vershueren, N. (2006).
Working memory capacity and a notorious brain teaser, Experimental Psychology, 53, 123-131.
-
DeNeys, W.(2006).
Developmental trends in decision making: The case of the Monty Hall dilemma. In J. A. Ellsworth (Ed.),
Psychology of decision making in education. Haupauge, NY:Nova Science Publishers.
-
Fox, C.R. & Levav, J. (2004).
Partition-edit-count: Naive extensional reasoning in judgment of conditional probability,
Journal of Experimental Psychology: General, 133, 626-642.
-
Friedman, D. (1998).
Monty Hall's three doors: Construction and desconstruction of a choice anomaly.
The American Economic Review, 88, 933-946.
(http://www.luiss.it/hey/ambiguity/papers/Friedman_1998.pdf )
-
Franco-Watkins, A. M. Derks, P. L., & Daugherty, M. R. P. (2003).
Reasoning in the Monty Hall problem:Examining choice behaviour and
probability judgements. Thinking and Reasoning, 9(1), 67-90.
-
Glymour, C.N. (2001).
The mind's arrow: Bayes nets and graphical causal models in psychology. MIT Press Cambridge.
-
Granberg, Donald and Brown, Thad A. (1995).
"The Monty Hall Dilemma," Personality and Social Psychology Bulletin 21(7): 711-729.
-
Granberg, Donald (1996).
"To Switch or Not to Switch". Appendix to vos Savant, Marilyn, The Power of Logical Thinking.
St. Martin's Press. ISBN 0-612-30463-3, (restricted online copy at Google Books).
ドナルド・グランバーグ著 「モンティ・ホール・ジレンマ ‐変えるべきか 変えざるべきか‐」
マリリン・ヴォス・サヴァント著 「気がつかなかった数学の罠 論理思考トレーニング法」東方雅美訳 中央経済社刊 (2002) の付録
-
服部雅史, 西田豊, 他. (2009年ごろ).
「確率判断と因果推論 Probability Judgment and Causal Inference」と銘打ったワークショップ
「基準率無視」に関する服部・西田両先生の説明の妥当性などを検討することが目的
高野陽太郎先生が企画者で、市川伸一先生も参加している
-
Herbranson, W. T. and Schroeder, J. (2010).
"Are birds smarter than mathematicians? Pigeons (Columba livia) perform
optimally on a version of the Monty Hall Dilemma." J. Comp. Psychol. 124(1): 1-13.
Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/20175592 March 1, 2010. http://people.whitman.edu/~herbrawt/HS_JCP_2010.pdf
-
Krauss, Stefan and Wang, X. T. (2003).
"The Psychology of the Monty Hall Problem:
Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser," Journal of Experimental Psychology: General 132(1).
Retrieved from http://www.usd.edu/~xtwang/Papers/MontyHallPaper.pdf March 30, 2008.
-
Johnson-Laird, P. N., Legrenzi, P., Girotto, V., Legrenzi, M. S., & Caverni, J.-P. (1999).
Naive probability: A mental model theory of extensional reasoning. Psychological Review, 106, 62-88.
-
三好一英・服部環 (2009).
確率判断課題/意思決定課題としてのモンティ・ホール・ジレンマ -数学から、心理学、そして行動経済学へ- .,筑波大学心理学研究 第37号
-
Miyake, A., Friedman, N. P., Rettinger, D. A., Shah, P., Hegarty,M. (2001).
How are visuospatial working memory,executive functioning,
and spatial abilities related? A latent-variable analysis.
Journal of Experimental Psychology:General, 130, 621-640.
-
Mueser, Peter R. and Granberg, Donald (May 1999).
"The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making",
University of Missouri Working Paper 99-06. Retrieved June 10, 2010.
-
Page, S.E. (1998).
Let's make a deal. Economic Leters, 61, 175-180.
-
Reed, S. K.(1993).
A schema-based theory of transfer.
In D. K. Detterman & R. J.Sternberg (Eds.), Transfer on trial: Intelligence, Cognition and Instruction (pp.39-37).
Norwood, NJ: Ablex.
-
Tubau, E. & Alonson, D. (2003).
Overcoming illusory inferences in a probabilistic counterintu-iteive problem:
The role of explicit representaitions. Memory & Cognition, 31, 596-607.
3囚人問題に関する心理学的研究の参考文献
-
Shimojo, S., & Ichikawa, S. (1989).
Intuitive reasoning about probability: Theoretical and experimental analysis of the “problem of three prisoners”. Cognition, 32, 1-24.
-
Ichikawa,S. & Takeichi, H. (1990).
Erroneous beliefs in estimating posterior probability. Behaviormetrika, Vol 27, Jan 1990, 59-73.
-
Falk, R.(1992).
A closer look at the probabilities of the notorious three prisoners, Cognition, 43, 197-223.
-
小林厚子 (1998).
確率判断の認知心理(1) 東京成徳大学研究紀要, 5, 89-100.
-
市川 伸一, 下條 信輔. (2010).
3囚人問題研究の展開と意義をふり返って . 認知心理学研究. 2010, Vol. 7, No. 2, p.137-145 .
-
寺尾敦・伊藤朋子 (2010).
3囚人問題はなぜ難しいのか-ベイズの定理学習後の解答分析, 日本教育心理学会第52回総会発表論文集, 691.
モンティ・ホール問題に関するその他の文献
-
Adams, Cecil (1990).
On 'Let's Make a Deal,' you pick Door #1. Monty opens Door #2—no prize.
Do you stay with Door #1 or switch to #3?",
The Straight Dope, (November 2, 1990). Retrieved July 25, 2005.
-
Bell, William (1992).
Comment on Let's make a deal by Morgan et al., American Statistician 46(3): 247 (August 1992).
-
Behrends (2008)
Behrends, Ehrhard (2008). Five-Minute Mathematics. AMS Bookstore. p. 57.
-
Devlin, Keith (July ‐ August 2003).
Devlin's Angle: Monty Hall.
The Mathematical Association of America. http://www.maa.org/devlin/devlin_07_03.html. Retrieved 2008-04-25.
-
Gardner, Martin (1982).
Three Scell Game, Aha! Gotcha book
-
Gill, Richard D.(2010).
The Monty Hall Problem is not a Probability Puzzle
-
Gill, Richard (2011)
The Monty Hall Problem. Mathematical Institute, University of Leiden, Netherlands 10-13, 17 March 2011. Eprint [3]
-
Gillman, Leonard (1992).
"The Car and the Goats," American Mathematical Monthly 99: 3–7.
-
ポール・ホフマン 『放浪の天才数学者エルデシュ』 平石律子訳、草思社文庫、(2011年10月)
原タイトル:The man who loved only numbers。
2000年4月の単行本の文庫版。
-
Hogbin, M. and Nijdam, W. (2010).
Letter to the editor, American Statistician. 64, 193
-
Klein, I. (1993),
Comment on Morgan et al. American Statistician, 47, 82-83.
-
Let's Make A Deal の公式サイトの "Monty Hall Problem "のページ
http://www.letsmakeadeal.com/problem.htm
-
Let's Make A Deal の公式サイトの "Show Info"のページ
http://www.letsmakeadeal.com/showinfo.htm
-
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991).
"Let's Make A Deal: The player's dilemma,"
American Statistician 45: 284-287.
-
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., & Doviak, M. J. (1991c).
REJOINDER TO VOS SAVANT
American Statistician 45: 347-348.
-
Morgan, J. P., Chaganty, N. R., Dahiya, R. C., and Doviak, M. J. (2010),
Response to Hogbin and Nijdam's letter, Am. Statist. 64 193-194.
-
Monty Hall(1975).
Steve Selvin の手紙に対する返事
http://www.letsmakeadeal.com/problem.htm
-
Nalebuff, Barry (1987).
"Puzzles: Choose a Curtain, Duel-ity, Two Point Conversions, and More,"
Journal of Economic Perspectives 1(2): 157-163 (Autumn, 1987).
-
Page, Lane (2005).
Perplexing question takes on a life of its own
(Craig F. Whitaker さんへの取材記事)
-
Rao, M. Bhaskara. (1992).
Comment on Morgan et al. American Statistician, 46, 241-242.
-
Bapeswara Rao, V. V. and Rao, M. Bhaskara (1992).
"A three-door game show and some of its variants".
The Mathematical Scientist 17(2): 89–94.
-
Rosenhouse, Jason.(2009).
The Monty Hall Problem. Oxford University Press.
日本語訳
ジェイソン・ローゼンハウス著 「モンティ・ホール問題」. 松浦俊輔訳、青土社.
-
Rosenthal, Jeffrey S. (2005a).
Monty Hall, Monty Fall, Monty Crawl. Math Horizons: September issue, 5–7.
Online reprint, 2008.
-
Rosenthal, Jeffrey S. (2005b)
: Struck by Lightening: the Curious World of Probabilities.
Harper Collings 2005, ISBN 978-0-00-200791-7.
-
Selvin, Steve (1975a).
"A problem in probability" (letter to the editor). American Statistician 29(1): 67 (February 1975).
-
Selvin, Steve (1975b).
"On the Monty Hall problem" (letter to the editor). American Statistician 29(3): 134 (August 1975).
-
Seymann R. G. (1991).
Comment on Let's make a deal: The player's dilemma, American Statistician 45: 287-288.
-
Tierney, John (1991).
"Behind Monty Hall's Doors: Puzzle, Debate and Answer?",
The New York Times, 1991-07-21. Retrieved on 2008-01-18.
http://www.nytimes.com/1991/07/21/us/behind-monty-hall-s-doors-puzzle-debate-and-answer.html?pagewanted=1
-
Vazsonyi, Andrew (1999).
"Which Door Has the Cadillac?," Decision Line, December/January 1999, 17–19.
-
vos Savant, Marilyn (1990).
"Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
-
vos Savant, Marilyn (1990b).
"Ask Marilyn" column, Parade Magazine p. 25 (2 December 1990).
-
vos Savant, Marilyn (1991).
"Ask Marilyn" column, Parade Magazine p. 12 (17 February 1991).
-
vos Savant, Marilyn (1991b).
MARILYN VOS SAVANT REPLY
American Statistician 45: 347.
-
vos Savant, Marilyn (1996).
The Power of Logical Thinking. St. Martin's Press. ISBN 0-312-15627-8.
-
Marilyn vos Savant による The Game Show Problem に関するWeb Page
http://www.marilynvossavant.com/articles/gameshow.html
-
Whitaker, Craig F. (1990).
[Formulation by Marilyn vos Savant of question posed in a letter from Craig Whitaker].
"Ask Marilyn" column, Parade Magazine p. 16 (9 September 1990).
3囚人問題に関するその他の文献
-
Gardner, Martin (1959a).
Mathematical Games column, Scientific American, October 1959, pp. 180–182.
Reprinted in The Second Scientific American Book of Mathematical Puzzles and Diversions.
-
Gardner, Martin (1959b).
Mathematical Games column, Scientific American, November 1959, p. 188.
-
Mosteller, Frederick (1987).
Fifty Challenging Problems in Probability.
Dover 1987 (reprint), ISBN 0-486-65355-2, p. 28-29 (restricted online version at Google Books)
-
Smith, John Maynard (1968).
Mathematical Ideas in Biology, Cambridge University Press, London, 1968.
確率の錯覚現象に関する文献
-
北岡 元 (2008).
仕事に役立つインテリジェンス (PHP新書
-
印南 一路 (2002).
すぐれた意思決定―判断と選択の心理学 (中公文庫
用語解説
-
標準仮定
モンティ・ホール問題や3囚人問題を数学的に解くためには問題文に明示的に書かれていない条件を仮定する必要がある。
標準仮定はそうした仮定の一つであり、モンティ・ホール問題の場合、次のような内容となっている。
①当たり扉はランダムかつ等確率に設定される
②ホストは挑戦者の選んだ扉を開けない
③ホストは必ず残りの扉を一枚開ける
④ホストはハズレの扉しか開けない
⑤ホストは挑戦者の選んだ扉が当たりのとき、ハズレ扉をランダムかつ等確率に選んで開ける
⑥ホストは扉を開けた後に必ずswitchの機会を挑戦者に与える
1975年に モンティ・ホール問題を発案した Steve Selvin も、
1990~1991年に PARADE誌のコラム"Ask Marilyn"で論争した人々の多くも、
標準仮定のもとに議論していた。
「標準仮定」(the standard assumptions)とは Wikipedia(英語版)の "Monty Hall problem"の記事で導入された言葉である。
3囚人問題の標準仮定は、「⑥ホストは扉を開けた後に必ずswitchの機会を挑戦者に与える」を除いたものになる。
-
等確率開扉の仮定
上記の標準仮定のうち、「⑤ホストは挑戦者の選んだ扉が当たりのとき、ハズレ扉をランダムかつ等確率に選んで開ける」を
私は「等確率開扉の仮定」と呼ぶことにしている。
3囚人問題の場合は、「⑤看守は質問した囚人が恩赦のとき、処刑される囚人からランダムかつ等確率に選んだ囚人の名を告げる」となる。
-
特定事象による条件付確率あるいは事後確率の解答
「特定事象による条件付確率あるいは事後確率の問題設定」の下での解答。
-
特定事象による条件付確率あるいは事後確率の問題設定
ホストが「これこれ」のハズレ扉を開けたとか、看守が「だれそれ」が処刑されると明かしたとかを証拠事象として、
「それぞれ」の扉が当たりである条件付き確率や、 「それぞれ」が恩赦になる条件付き確率を計算する問題設定である。
-
不特定事象による条件付確率あるいは事後確率の解答
「不特定事象による条件付確率あるいは事後確率の問題設定」の下での解答。
-
不特定事象による条件付確率あるいは事後確率の問題設定
ホストが「いずれか」のハズレ扉を開けたとか、看守が「いずれか」の処刑される囚人の名を明かしたとかを証拠事象として、
「挑戦者が選んだ」扉、あるいは「残りの」扉が当たりである条件付き確率や、 「質問した」囚人、あるいは「残りの」囚人が恩赦になる条件付き確率を計算する問題設定である。
-
非条件付確率の解答
「非条件付確率の問題設定」の下での解答。
-
非条件付確率の問題設定
ホストが「いずれか」のハズレ扉を開けるとか、看守が「いずれか」の処刑される囚人の名を明かすことは最初から分っていることとして
(相場用語なら「織り込み済み」だとして)
「挑戦者が選んだ」扉、あるいは「残りの」扉が当たりである確率や、 「質問した」囚人、あるいは「残りの」囚人が恩赦になる確率を計算する問題設定である。
証拠事象によって標本空間の絞込みを行わない点が、「不特定事象による条件付確率あるいは事後確率の問題設定」との大きな違いである。
-
戦略に着目した解答
「戦略に着目した問題設定」の下での解答。
-
戦略に着目した問題設定
モンティ・ホール問題特有の問題設定である。
Let's Make A Deal の入場券を持っているが都合が悪くなって兄弟に代わりに参加してもらうときに、
「もしも挑戦者に選ばれたら必ずswitchする」ことを託して賞品を得る確率である。
switch させてもらえなかったけれど賞品を得ることができた場合」も含んで計算する点が非条件付確率の問題設定と異なっている。
-
初期事象
私の造語である。
モンティ・ホール問題の場合の当り扉に関する3つの事象、「扉1が当り」、「扉2が当り」、「扉3が当り」や、
3囚人問題の場合の恩赦になる囚人に関する3つの事象、「囚人A,が恩赦」、「囚人Bが恩赦」、「囚人Cが恩赦」を統一的に表している。
-
中間事象
私の造語である。
モンティ・ホール問題の場合の挑戦者が選んだ扉に関する3つの事象、「挑戦者が扉1を選んだ」、「挑戦者が扉2を選んだ」、「挑戦者が扉3を選んだ」や、
3囚人問題の場合の看守に質問した囚人に関する3つの事象、「囚人A,が質問した」、「囚人Bが質問した」、「囚人Cが質問した」を統一的に表している。
-
対戦型形式と標準型形式
標準型:扉が3枚あって、挑戦者もホストも扉の同じ側にいる形式のモンティ・ホール問題
対戦型:カードが3枚あって、最初に1枚のカードを選ぶ者と、残りのカードを2枚手にする者が相対して行う形式のモンティ・ホール問題
対戦型で最初に1枚のカードを選ぶ者はカードの表を見ることができないが、残りの2枚のカードを手にする者はカードの表を見ることができる。
Tubau, E. & Alonson, D. (2003). が、この二つのタイプの問題文を使って実験を行い、正答率の差を見出している。
-
ボクサー型ゲーム形式
ボクサー型とは Burns, B.D. & Wieths, M. (2004). の実験で使われた次のようなゲーム形式である。
3人のボクサーが勝ち抜き戦を行う。
一人のボクサーは残りのどちらにも勝つが誰がそのボクサーかはわからない。
最初の試合で勝ったボクサーと、まだ試合をしていない残りのボクサーのどちらが勝つ確率が高いかを予想させる。
-
地獄から来たモンティ
モンティ・ホール問題のホストの行動パターンが標準仮定から外れているパターンの一種で、
挑戦者が当り扉を選んだときには switch の機会が与えられるが、ハズレ扉を選んだときには与えられないパターンを言う。
-
天使モンティ
モンティ・ホール問題のホストの行動パターンが標準仮定から外れているパターンの一種で、
挑戦者がハズレ扉を選んだときには switch の機会が与えられるが、当り扉を選んだときには与えられないパターンを言う。
-
夕食問題
市川 伸一, 下條 信輔. (2010). 3囚人問題研究の展開と意義をふり返って . 認知心理学研究. 2010, Vol. 7, No. 2, p.137-145 で、
橋田浩一氏が提案した「夕食問題」を次のように紹介している。、
「夕食のオカズがイカ、マグロ、サンマのうちどれか1品である、それぞれの確率が 1/4、 1/4、 1/2 であるとする。
調理法としては、「イカは焼くかナマかの確率が 1/2 ずつ」「マグロは必ずナマ」「サンマは必ず焼く」ということが分っている。
いま、帰宅時に家から煙があがっているのが見えたとき、今日のオカズがイカである確率はどれだけか」
-
先刻承知確率不変説の過剰適用
私の造語である。
ホストがハズレの扉を開けることは最初から分かっているので、挑戦者が選らんだ扉が当たりである確率は変わらないとする説明の仕方を
「先刻承知確率不変説」 と私は呼ぶことにしている。
挑戦者が選んだ扉だけでなく、ホストが開いた扉まで特定しながらこの論法で説明するためには
扉の間の対称性も理由として上げなければならない。
そうした配慮が欠けている説明の仕方を 「先刻承知確率不変説の過剰適用」 と私は呼ぶことにしている。
-
確率継承説
ホストが開ける扉の範囲が挑戦者が選ばなかった扉の範囲に限定されているので、
挑戦者が選ばなかった扉のどちらかが当たりである確率がホストが開け残した扉に継承されるという説明の仕方である。
ホストが開けた扉や開け残した扉を特定した説明をしていながら、きちんとした条件付き確率の計算になっていないことが多い。
-
客観確率幻想
私の造語である。
標本空間を分割してできる事象ではなく、何かの実体や現象が確率を担うという幻想を表しています。
モンティ・ホール問題の場合で言えば、「扉1が当たり」という「事象」でなく、「扉1そのもの」という実体に確率が割り付けられているという幻想がそれにあたります。
-
客観期待値幻想
私の造語である。
これは、人間が期待値を考えるとき、あたかもエネルギーや質量、あるいはカードのポイントのように
保存される量として期待値が宿ると考えているのだ、 という説を表している。
二つの封筒問題で惹起される錯覚現象の中に 「期待値の錯覚」 現象がある。 (二つの封筒問題の錯覚に気づかない人のために 参照)
その 「期待値の錯覚」 の背後に、「客観期待値幻想」 が潜んでいるのではないかと、私は思っている。
目次に戻る
トップページに戻る