トップページに戻る
「モンティ・ホール問題」 がどんな問題で、どうして扉を替えた方が有利なのか、 一応理解している人を対象に書いています。
ここでも分数を使っていないので、小学生でもわかるかも知れません。
時間の流れとともに条件が絞られていく問題を考えるときに、普通の人がとるとらえ方です。
ホストが開けた扉を区別しないこの考え方は、よほどパズル慣れしていないと出来ないとらえ方です。
ホストが必ずハズレの扉を開けてくれるなら、次の非条件付確率の問題としてのとらえ方と見た目では区別が付きません。
将来のこととして考えるのは、よほどギャンブルに強い人でないとできないとらえ方です。
「場合の数」を数えるだけで解けてしまうので、通俗的な説明で一番よく使われています。
上記の他に、ハズレの賞品を区別するとらえ方もあります。
例えば、当りの扉の賞品が自動車で、ハズレの扉の賞品がヤギの場合、2頭のヤギに名前を付けてから問題を考える人もいます。
しかし、モンティ・ホール問題はもともとハズレの扉(もともとは箱)に何も入っていないので、このとらえ方では一般性がありません。
その一部をご紹介します。
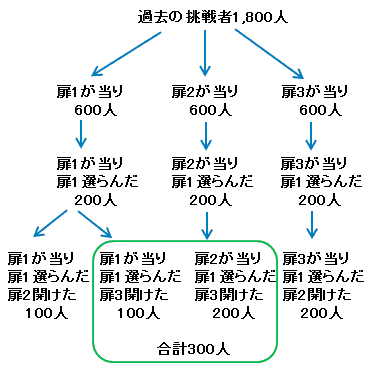
あなたの前に、1800人の人がこのゲームに挑戦していたとしましょう。
このようにして、あなたの前にこのゲームをして、あなたと同じように扉1を選んで、あなたと同じようにホストが扉2 または扉3 を開けた人たちのうち、扉を替えた方がよい人は、 替えない方がよい人の2倍いたことがわかります。
このデータから、あなたの場合も替えたときに賞品をゲットする可能性が、替えないでゲットする可能性の 2倍だということがわかりました。
あなたの前に、1800人の人がこのゲームに挑戦していたとしましょう。
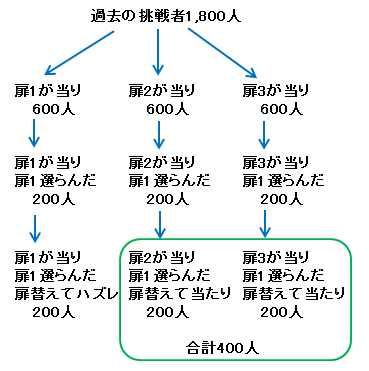
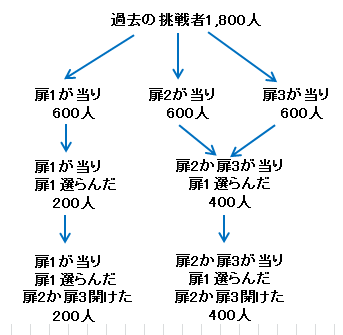
このようにして、あなたの前にこのゲームをして、あなたと同じように扉1を選んだ人たちのうち、扉を替えた方がよい人は、 替えない方がよい人の2倍いたことがわかります。
このデータから、あなたの場合も替えたときに賞品をゲットする可能性が、替えないでゲットする可能性の 2倍だということがわかりました。
当たり扉の決め方で扉の間に偏りがなく、ハズレ扉をホストが開ける開け方にも偏りがないという条件の場合、これらの3つのとらえ方の答えが一致します。
まず、「非条件付確率の問題としてのとらえ方」 から見て行きます。
非条件付確率の問題としてのとらえ方

扉1以外が当たりでも扉1が当たりでも、ホストは扉2か扉3を開けるので、「非条件付確率の問題としてのとらえ方」 の図は 「ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方」 の図と一致します。
ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方

ホストによるハズレ扉の開け方を見ると、 扉1が当たりのときの扉2と扉3の間に対称性があり、扉1以外が当たりのときの扉2と扉3の間にも対称性があるので、 「ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方」 の図を左右対称に 分割すると 「条件付確率の問題としてのとらえ方」 が出来上がります。
条件付確率の問題としてのとらえ方
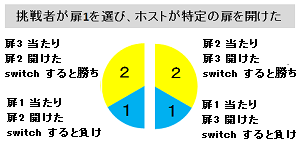
モンティ・ホール問題には数学の問題がいくつも潜んでいたのです。
ホストの行動パターンの条件を変えると、それぞれの計算結果が違ってくることから、 これらが別個の問題であることがわかります。
ホストがハズレの扉を開けるとき扉を選り好みする条件にすると、 条件付き確率の問題としてのとらえ方と他のとらえ方で計算結果が異なってきます。
ホストがハズレ扉を開けるとは限らない条件にすると、 非条件付き確率の問題としてとらえられなくなります。
Web上のわかりやすい説明 でブログなどで見かけたわかりやすい説明を集めています。
条件付き確率の問題としてのとらえ方での説明や、非条件付き確率の問題としてのとらえ方での説明も載っています。
トップページに戻る
2013/08/18 14:36:29
中学生にもわかるモンティ・ホール問題
ここでは、モンティ・ホール問題の数学的なとらえ方に種類があることをご説明します。「モンティ・ホール問題」 がどんな問題で、どうして扉を替えた方が有利なのか、 一応理解している人を対象に書いています。
ここでも分数を使っていないので、小学生でもわかるかも知れません。
モンティ・ホール問題のおさらい
1990年にアメリカの雑誌 「パレード」 のコラム 「マリリンに聞こう」 で議論された問題文は大体、こんな感じです。
あなたはテレビのゲーム番組に挑戦者として出ています。
三つの扉の一つに賞品が隠されています。
あなたは扉を一つ選びます。
もしもあなたが選んだ扉に賞品があればあなたのものになります。
あなたが扉1を選んだとしてください。
そうすると、ホストは残りの扉のうちハズレの扉、たとえば扉3を開けます。
あなたに扉を選び直す権利が与えられます。
あなたは扉1 から扉2 に替えた方が有利でしょうか?
三つの扉の一つに賞品が隠されています。
あなたは扉を一つ選びます。
もしもあなたが選んだ扉に賞品があればあなたのものになります。
あなたが扉1を選んだとしてください。
そうすると、ホストは残りの扉のうちハズレの扉、たとえば扉3を開けます。
あなたに扉を選び直す権利が与えられます。
あなたは扉1 から扉2 に替えた方が有利でしょうか?
モンティ・ホール問題の数学的なとらえ方
主要なとらえ方には次の3種類があります。条件付確率の問題としてのとらえ方
挑戦者が選んだ扉とホストが選んだ扉を限定して、その中で挑戦者が扉を替えた方が有利かどうかを考えます。時間の流れとともに条件が絞られていく問題を考えるときに、普通の人がとるとらえ方です。
ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方
挑戦者が選んだ扉は限定するが、ホストが選んだ扉はどちらでもよいとして、その中で挑戦者が扉を替えた方が有利かどうかを考えます。ホストが開けた扉を区別しないこの考え方は、よほどパズル慣れしていないと出来ないとらえ方です。
ホストが必ずハズレの扉を開けてくれるなら、次の非条件付確率の問題としてのとらえ方と見た目では区別が付きません。
非条件付確率の問題としてのとらえ方
ホストが扉を開ける前の段階で、将来ホストが扉を開けたら挑戦者はどうしたらよいかを考えます。将来のこととして考えるのは、よほどギャンブルに強い人でないとできないとらえ方です。
「場合の数」を数えるだけで解けてしまうので、通俗的な説明で一番よく使われています。
上記の他に、ハズレの賞品を区別するとらえ方もあります。
例えば、当りの扉の賞品が自動車で、ハズレの扉の賞品がヤギの場合、2頭のヤギに名前を付けてから問題を考える人もいます。
しかし、モンティ・ホール問題はもともとハズレの扉(もともとは箱)に何も入っていないので、このとらえ方では一般性がありません。
条件付確率の問題としてのとらえ方での解法
小学生にもわかるモンティ・ホール問題 で説明しています。その一部をご紹介します。
ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方での解法
この部分を 2013/08/12 に書き換えました。あなたの前に、1800人の人がこのゲームに挑戦していたとしましょう。
このようにして、あなたの前にこのゲームをして、あなたと同じように扉1を選んで、あなたと同じようにホストが扉2 または扉3 を開けた人たちのうち、扉を替えた方がよい人は、 替えない方がよい人の2倍いたことがわかります。
このデータから、あなたの場合も替えたときに賞品をゲットする可能性が、替えないでゲットする可能性の 2倍だということがわかりました。
非条件付確率の問題としてのとらえ方での解法
この部分を 2013/08/12 に書き換えました。あなたの前に、1800人の人がこのゲームに挑戦していたとしましょう。
このようにして、あなたの前にこのゲームをして、あなたと同じように扉1を選んだ人たちのうち、扉を替えた方がよい人は、 替えない方がよい人の2倍いたことがわかります。
このデータから、あなたの場合も替えたときに賞品をゲットする可能性が、替えないでゲットする可能性の 2倍だということがわかりました。
とらえ方が違っても答えが一致する理由
この部分を 2013/08/04 に書き足しました。当たり扉の決め方で扉の間に偏りがなく、ハズレ扉をホストが開ける開け方にも偏りがないという条件の場合、これらの3つのとらえ方の答えが一致します。
まず、「非条件付確率の問題としてのとらえ方」 から見て行きます。
非条件付確率の問題としてのとらえ方
扉1以外が当たりでも扉1が当たりでも、ホストは扉2か扉3を開けるので、「非条件付確率の問題としてのとらえ方」 の図は 「ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方」 の図と一致します。
ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方
ホストによるハズレ扉の開け方を見ると、 扉1が当たりのときの扉2と扉3の間に対称性があり、扉1以外が当たりのときの扉2と扉3の間にも対称性があるので、 「ホストが開けた扉は特定しない条件付確率の問題としてのとらえ方」 の図を左右対称に 分割すると 「条件付確率の問題としてのとらえ方」 が出来上がります。
条件付確率の問題としてのとらえ方
これらのとらえ方の違いは単なる「解き方の違い」ではない
上記の三つのとらえ方は単なる「解き方の違い」ではなく、まったく別個の問題になっていることに気付くことが重要です。モンティ・ホール問題には数学の問題がいくつも潜んでいたのです。
ホストの行動パターンの条件を変えると、それぞれの計算結果が違ってくることから、 これらが別個の問題であることがわかります。
ホストがハズレの扉を開けるとき扉を選り好みする条件にすると、 条件付き確率の問題としてのとらえ方と他のとらえ方で計算結果が異なってきます。
ホストがハズレ扉を開けるとは限らない条件にすると、 非条件付き確率の問題としてとらえられなくなります。
お勧めのページ
条件付き確率の問題としてのとらえ方での説明や、非条件付き確率の問題としてのとらえ方での説明も載っています。
トップページに戻る