トップページに戻る
2013/12/29 に 「条件付交換利得の基本」 という項を設け、 「「封筒を開けてから交換型」 の二封筒問題」 という項や 「パラドキシカル分布」 という項の内容の一部を移動しました。
2013/12/30 に 「条件付きでない交換利得の期待値」 という項を追加しました。
2014/01/01 に 条件付き交換利得の期待値と条件付でない交換利得の期待値の関係に着目して全体の構成を見直しました。
2014/11/29 に 条件付き交換利得の期待値を確率分布関数で表現する項を設けました。
「封筒を開ける前に交換型」と「封筒を開けてから交換型」のニ封筒問題のそれぞれの錯覚現象について調べる前に、二封筒問題の数学について基本を押さえました。
そして、同確率条件を満たす金額分布は存在しません。
つまり、二封筒問題のパラドックスのように、選んだ封筒の金額に対して、封筒を交換したときに倍増したり半減したりする確率がどちらも ½ だなどということは現実にはあり得ません。
これについては、付録の 「金額の上限を無くしても同確率条件は成立しなそうだ」 で詳しく論じています。
「期待交換利得ゼロ条件」とは選んだ封筒の金額を条件とする封筒交換後の金額の期待値が選んだ封筒の金額に等しいことが選らんだ封筒の金額によらず常に成立することを表す、私の造語です。
そして、期待交換利得ゼロ条件を満たす金額分布は存在しません。
つまり二封筒問題を論じる人がよく陥る錯覚 「封筒を開けて金額がわかっても封筒を交換することに意味はない」 などということは現実にはあり得ません。
これについては Amos Storkey というエジンバラ大学の先生による"Amos Storkey - Brain Teasers: Two Envelope Paradox - Solution " というWebページが参考になります。
離散的な場合
k = 2 の場合に試しに g(m) = g(m/2) と置いてみると、上の式がパラドックスな値 0.25 m に一致するので正しそうです。
連続的な場合
連続的な場合に高額側の金額である事後オッズの式に係数1/k が現れるわけは、次の図を見ると納得できると思います。
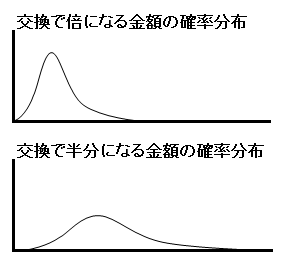
積分の変数変換の公式を思い出しながら計算して確かめる人もいらっしゃるでしょう。
あるいは、次の資料も参考になるでしょう。
と証明されています。 つまり、金額の平均値が無限大であることがパラドキシカル分布であることの条件だということです。
また、交換して手に入る金額の平均値から交換しないで手に入る金額の平均値を引いた値のゼロとも一致します。
交換して手に入る金額の平均値から交換しないで手に入る金額の平均値を引いた値がゼロであることについてはついて、「封筒を開ける前に交換型」の場合、金額の平均値が有限の場合に封筒を交換しても期待値に変わりがないことで計算してみました。∞ − ∞ ということになり、値は定まりません。
金額分布が離散的な場合に、「条件付きでない交換利得の期待値」 として選んだ封筒に入っている金額 x が少額側の場合と高額側の場合を区別した全ての場合について交換利得と確率の積の総和を計算するための数列の和の式を立てると、数列の和の項のグルーピングを変えると和の値が変わるという現象が起きます。
それに関連して、Norton, J.D. 1998. に非常に面白い発見が書かれているので Jhon D. Norton の論文に見る数列の和の項のグルーピング問題でご紹介します。
その理由について、付録の 金額の平均値が有限のとき交換利得の条件付き期待値の期待値は交換利得の期待値か で考えてみました。
このことから、「封筒を開けてから交換型」のゲームを反復した場合の 「条件付き交換利得の期待値の平均」 が、 「封筒を開ける前に交換型」のゲームにおける 「条件付きでない交換利得の期待値」 に近づいていくことがわかります。
ゲーム回数 n を増やしても平均交換利得がゼロに近かないどころか、ますます幅が広がって行くことがあることが、Norton, J.D. 1998. を読むとわかります。
ゲーム回数 n を増やすと平均交換倍率について書かれた論文を見たことがありませんが 1 に近づかも知れないと思います。しかし大数の法則も成立しなそうなので、近づかないかも知れません。
しかし! 「パラドックス」と呼ばれるほど不思議なため、証明したがる人が少なくありません。
かく言う私もその一人です。
封筒を交換しても意味がないことを数学的に証明する方法は、確率分布に差異がないことを示す方法と、期待値に差異がないことを示す方法があります。
2013/12/31 に以降の構成を整頓しました。
2013/09/22 に下記の一部を訂正しました。
2013/11/17 に次の行を追加しました。
その後しばらくたってから、この証明や類似の証明を根拠に二封筒問題のパラドックスが解決されたと主張する人が多いことに気づきました。
そういう人たちにとっては「定義」ではなく、あくまでも「証明」なのでしょう。
金額の平均値が無限大の場合には、Norton, J.D. 1998. に書かれているように、 「条件付きでない交換利得の期待値」 を計算する式の値が定まらないので、「期待値」は開ける前の二つの封筒の互角性を判断する基準にできなそうです。
「期待値」あるいはその他の方法によって平均値無限大の二つの封筒の優劣の有り無しを説明する方法を探る研究が色々されていますが、まだ未解決の問題のようです。
Norton, J.D. 1998.
Clark, Michael. & Shackel, Nicholas. (2000).
Chalmers, David J. (2002).
余談
効用の平均値無限大の世界では期待値は無意味だということを、数学者や意思決定論者が認めれば済んでしまう問題かも知れません。
例として、金額ペアの確率分布が次のようだとします。
このような確率分布で「封筒を開けてから交換型」の二封筒問題を考えると、小額側ペアの事後オッズと高額側ペアの事後オッズが等しくても、交換した方が有利になります。
たとえば、兄弟の片方の金額が 2 で、他方の金額が 4 なら、それぞれの立場に立って考えると、両者とも交換した方が有利になります。
これを不思議に感じる気持ちの方こそ不思議なのです。
二封筒問題のパラドキシカル分布参照
同じ確率分布で「封筒を開ける前に交換型」の二封筒問題を考えたら、こちらの方も常に交換した方がよいのではないかと思えて、封筒を開ける前には二つの封筒が互角だという確信がゆらいできます。
パラドキシカル分布の謎参照
ここでは、「金額着目型」の考え方で計算してみました。少額金額に対する高額金額の倍率をkとする。
封筒に入る可能性のある金額を x とする。
金額 x が少額側の金額である確率をa(x) とする。
x が高額側の金額である確率をb(x) とする 。
b(x) = a(x/k) である 。
封筒を交換しなかったときの期待値をEとすると
E = (xa(x)/2 + xb(x)/2)の総和
= (xa(x)/2 + xa(x/k)/2)の総和。
項別の総和に分割して、
E = (xa(x)の総和 + (k(x/k)a(x/k))の総和)/2。
E =xa(x) (1 + k)/2の総和。
封筒を交換したときの期待値をCとすると
C = ((x/k)b(x)/2 + kxa(x)/2)の総和
項別の総和に分割して、
= (x/k)a(x/k)の総和 + kxa(x)の総和)/2。
C = xa(x)の総和 + kxa(x)の総和)/2。
C =xa(x) (1 + k)/2の総和。
よって、E=C となり、封筒を交換してもしなくても期待値が変わらないことがわかりました。少額金額に対する高額金額の倍率をkとする。
封筒に入る可能性のある金額を x とする。
金額 x が少額側の金額である確率密度関数をa(x) とする。
x が高額側の金額である確率密度関数をb(x) とする 。
b(x) = (1/k)a(x/k) である 。
封筒を交換しなかったときの期待値をEとすると
E = (xa(x)/2 + xb(x)/2)の積分
= (xa(x)/2 + (1/k)xa(x/k)/2)の積分。
項別の積分に分割して、
E = (xa(x)の積分 + (1/k)(k2xa(x))の積分)/2。
E =xa(x) (1 + k)/2の積分。
封筒を交換したときの期待値をCとすると
C = ((x/k)b(x)/2 + kxa(x)/2)の積分
項別の積分に分割して、
= (x/k)(1/k)a(x/k)の積分 + kxa(x)の積分)/2。
C = kx(1/k)a(x)の積分 + kxa(x)の積分)/2。
C =xa(x) (1 + k)/2の積分。
よって、E=C となり、封筒を交換してもしなくても期待値が変わらないことがわかりました。
金額分布が離散的な場合
選んだ封筒に入っている金額にそれが少額側か高額側かを組み合わせたものが素事象に対応するとします。
ある素事象について、少額側か高額側かを反転させた素事象を対事象と呼ぶことにします。
封筒を交換しない場合の期待値をEとすると
E = 各素事象ごとの金額とその確率の積の総和。
封筒を交換した場合の期待値をCとすると
C = 各素事象ごとの対事象の金額とその確率の積の総和。
上のそれぞれの式の項の間に対応関係があるので、 金額の期待値が有限の場合にはE=C となり、封筒を交換してもしなくても期待値が変わらないことがわかりました。
金額分布が連続的な場合
やや、ややこしいので割愛します。
各素事象に効用が割り当てられていて、その期待値が関心の対象だとします。
期待値 = 全素事象の効用と確率の積の総和
全事象が排他的な証拠事象に分割されたとします。
条件付き期待値 = その証拠事象の素事象の効用と確率の積の和 / その証拠事象の確率
条件付き期待値の期待値 = 条件付き期待値とその証拠事象の確率の積の総和
よって、
条件付き期待値の期待値
= (各証拠事象の素事象の効用と確率の積の和)の総和
= 全素事象の効用と確率の積の総和
= 期待値
各素事象ごとに封筒を交換したときの金額の増分を効用と考え、交換利得と呼ぶことにします。
交換利得の期待値をEとすると
E = 各素事象ごとの交換利得とその確率の積の総和。
この式の項はある金額に関して少額側の項と高額側の項が対になっているので、 全事象を通した金額の期待値が有限の場合には、それらが打消し合うことにより、E = 0 となります。
選んだ封筒に入っている金額を証拠事象とした交換利得の条件付き期待値の期待値が期待値E になるので、
全事象を通した金額の期待値が有限の場合には
選んだ封筒の金額ごとの交換利得の条件付き期待値の金額全体での期待値 が 0 であることになります。
パラドキシカル分布の場合にはこのようなことがないのは、いうまでもありません。
二封筒問題のパラドキシカル分布
選んだ封筒に x という金額が入っていたとします。そうすると、もしも同確率条件が成立するならば、2nx と 2n+1x の金額のペア ( n は任意の整数)
の全てが封筒に入る可能性があることになります。
(2nx, 2n+1x) のペアのうち、2nx の方に同確率条件が成立するとすると(2n-1x, 2nx) の
ペアと (2nx, 2n+1x) のペアの両方が同確率で発生することになります。
ということはこうして出来た全ての金額ペアが同確率で発生することになるので、 それらの確率の総和が無限大に発散します。
ゆえに全ての金額ペアの確率の総和も無限大に発散します。
ゆえに、離散的な金額分布の場合には同確率条件は成立しません。Q.E.D
次に金額分布が連続で確率密度関数も連続な場合を考えてみました。
金額ペア (x, 2x) の確率密度関数を g(x) とすると
少額側の金額 s 単独の確率密度関数は g(s) で、
高額側の金額 k 単独の確率密度関数は g(k/2)/2 。
よって、同確率条件から、2g(x) = g(x/2)。 (※1)
よってg(x) = a / x となりますが、 (※2)
この関数を積分すると無限大になってしまいます。
ゆえに、連続的な金額分布の場合にも同確率条件は成立しません。Q.E.D
※1 Chalmers, D.J. 1994. にも同じ式が出て来ます。Chalmers の論文
※2 g(x) = a / x という式が必ず導かれるか余り自信ありませんが、一つの例ではあるし、 統計学博士の美添泰人さんのホームページからリンクされている 「確率に関するパラドックス(その1)」 という表題の pdf ファイルでも同じ関数が導かれているので、間違いないでしょう。
金額分布が連続的な場合の計算にあやふやなところがありますが、同確率条件が成立しなそうだという気にはなります。
この問題に関する論文を調べれば、もしかしたら同確率条件が成立する確率分布が発見されているかも知れませんが、それもなさそうな話です。
もしそうなら色々な論文で紹介しているだろうからです。
トップページに戻る
2014/12/02 23:56:16
初版 2013/09/05
二封筒問題の数学
2013/12/28 に 「金額分布の基本」 という項を設けました。2013/12/29 に 「条件付交換利得の基本」 という項を設け、 「「封筒を開けてから交換型」 の二封筒問題」 という項や 「パラドキシカル分布」 という項の内容の一部を移動しました。
2013/12/30 に 「条件付きでない交換利得の期待値」 という項を追加しました。
2014/01/01 に 条件付き交換利得の期待値と条件付でない交換利得の期待値の関係に着目して全体の構成を見直しました。
2014/11/29 に 条件付き交換利得の期待値を確率分布関数で表現する項を設けました。
「封筒を開ける前に交換型」と「封筒を開けてから交換型」のニ封筒問題のそれぞれの錯覚現象について調べる前に、二封筒問題の数学について基本を押さえました。
二封筒問題のおさらい
「封筒を開ける前に交換型」の二封筒問題とは次のような錯覚現象を言います。- お金もしくは小切手の入った二つの封筒があり、一方には他方の倍の金額が入っている。
- どちらが大きな金額か知らないでランダムに封筒を選ぶと中身がもらえる。
- 選らんだ封筒の中身を x とすると、もう片方の中身は
確率 1/2 で x/2、確率 1/2 で 2x だ。 - だから選ばなかった方の金額の期待値は
(1/2)(x/2) + (1/2)2X = 1.25x で x より大きい。 - 選ばなかった方の金額の期待値の方が大きいから封筒を替えさせてもらおう。
- その後で同じことを考えるので永久に封筒を替え続けることになってしまう???
- 不思議だ。
- お金もしくは小切手の入った二つの封筒があり、一方には他方の倍の金額が入っている。
- どちらが大きな金額か知らない二人の兄弟がランダムに別々の封筒を選ぶ。
- 二人は相手に分からないようにして封筒の中身を見る。
- 兄弟の一人の封筒の中身は x だったので、次のように考えた。
- もう一人の封筒の中身は
確率 1/2 で x/2、確率 1/2 で 2x だ。 - だからもう一人の封筒の金額の期待値は
(1/2)(x/2) + (1/2)2X = 1.25x で x より大きい。 - もう一人の封筒の金額の期待値の方が大きいから封筒を交換することを提案しよう。
- 兄弟ともに同じことを考える???
- 不思議だ。
金額分布の基本
同確率条件が成立する金額分布は存在しない
「同確率条件」とは選んだ封筒の金額 x に対して、選ばなかった封筒の金額が x/2 である確率も、2x である確率もともに ½ であることが、金額 x によらず常に成立すことを表す、私の造語です。そして、同確率条件を満たす金額分布は存在しません。
つまり、二封筒問題のパラドックスのように、選んだ封筒の金額に対して、封筒を交換したときに倍増したり半減したりする確率がどちらも ½ だなどということは現実にはあり得ません。
これについては、付録の 「金額の上限を無くしても同確率条件は成立しなそうだ」 で詳しく論じています。
期待交換利得ゼロ条件が成立する金額分布は存在しない
2013/12/29 に 「同期待値条件」 という用語を 「期待交換利得ゼロ条件」 に改めました。「期待交換利得ゼロ条件」とは選んだ封筒の金額を条件とする封筒交換後の金額の期待値が選んだ封筒の金額に等しいことが選らんだ封筒の金額によらず常に成立することを表す、私の造語です。
そして、期待交換利得ゼロ条件を満たす金額分布は存在しません。
つまり二封筒問題を論じる人がよく陥る錯覚 「封筒を開けて金額がわかっても封筒を交換することに意味はない」 などということは現実にはあり得ません。
これについては Amos Storkey というエジンバラ大学の先生による"
条件付き交換利得の期待値の基本
選んだ封筒の金額を条件とする交換利得の期待値を 「条件付き交換利得の期待値」 と呼ぶことにします。条件付き交換利得の期待値に関する一般式
選んだ封筒の金額を条件とした場合に交換が有利か否かを判別する一般式は次のようになります。
二つの封筒に入っている小額の金額と高額の金額の倍率を k とする。
2013/09/22 に次の行を訂正しました。
封筒に入っていた金額を m として、金額ペア(m/k, m) と (m, km) をそれぞれ小額側ペアと高額側ペアと呼ぶことする。
封筒を切り替えた後の金額の封筒に入っていた金額を証拠事象とする条件付き平均倍率 を CEM (Conditionally Expected Magnification) と書くことにする。
小額側ペアの事後オッズを s 、高額側ペアの事後オッズを b とすると、
CEM =(s/k)/( s + b) + kb/(s + b) =
(s/k + kb)/(s + b)
となる。
(CEM − 1)m が条件付き交換利得である。
注:選ばなかった封筒の金額の条件付き期待値から選んだ封筒の金額を引いたものが条件付き交換利得です。
CEM の値が 1 より大なら封筒を交換すると有利になるので、それを不等式で表すと、次のようになる。
s/k + kb > s + b
すなわちs < kb
これが、選んだ封筒の金額を条件とした場合に交換が有利か否かを判別する一般式である。
2013/09/22 に次の行を訂正しました。
封筒に入っていた金額を m として、金額ペア
封筒を切り替えた後の金額の封筒に入っていた金額を証拠事象とする条件付き平均倍率 を CEM (Conditionally Expected Magnification) と書くことにする。
CEM =
となる。
(CEM − 1)m が条件付き交換利得である。
注:選ばなかった封筒の金額の条件付き期待値から選んだ封筒の金額を引いたものが条件付き交換利得です。
CEM の値が 1 より大なら封筒を交換すると有利になるので、それを不等式で表すと、次のようになる。
すなわち
これが、選んだ封筒の金額を条件とした場合に交換が有利か否かを判別する一般式である。
条件付き交換利得の期待値を確率分布関数で表現した場合
確率分布が離散的な場合と連続的な場合の二通りを考えてみます。離散的な場合
最もポピュラーな確率分布の表現方法は、金額ペアの小さい方の金額 x に対して g(x) で確率を表す方法です。
二つの封筒問題の場合、金額ペアが定まった場合に、少額と高額のどちらを選ぶかの尤度比は1 対 1 なので、封筒に入っていた金額を m と置くと、事後オッズは次のようになります。
s = g(m) , b = g(m/k)
したがって、条件付き交換利得の期待値は次のようになります。
(CEM − 1)m = (((s/k + kb) /(s + b)) − 1)m =
(k − 1)(kb − s)m / (k(s + b)) =
(k − 1)(kg(m/k) − g(m))m / (k(g(m) + g(m/k))
k = 2 の場合は
(g(m/2) − g(m) / 2)m / (g(m) + g(m/2))
二つの封筒問題の場合、金額ペアが定まった場合に、少額と高額のどちらを選ぶかの尤度比は
したがって、条件付き交換利得の期待値は次のようになります。
k = 2 の場合は
連続的な場合
離散的な場合に合わせて、金額ペアの少額の金額に関する関数で確率密度を表してみます。
離散的な場合の確率分布関数 g を確率密度関数と読み替えると、次のようになります。
s = g(m) , b = g(m/k)/k
高額側の金額である事後オッズの式が離散的な場合と異なるだけで、後はまったく同じ理屈になります。
離散的な場合の確率分布関数 g を確率密度関数と読み替えると、次のようになります。
高額側の金額である事後オッズの式が離散的な場合と異なるだけで、後はまったく同じ理屈になります。
連続的な場合に高額側の金額である事後オッズの式に係数
積分の変数変換の公式を思い出しながら計算して確かめる人もいらっしゃるでしょう。
あるいは、次の資料も参考になるでしょう。
- 統計学博士の美添泰人さんのホームページ 「美添泰人のホームページ [青山学院大学 経済学部]」 の 「統計に関する教材」 というページからリンクされている 「確率に関するパラドックス(その1)」 という表題の pdf ファイル
条件付き交換利得に関する制約
Broome,John.(1995). の付録Bで、金額の平均値が有限の場合、
「開けた封筒の金額 x を証拠事象とする残りの封筒の金額の事後期待値が x より大きいことが、 すべての x ついて成り立つ」
ことはない
「開けた封筒の金額 x を証拠事象とする残りの封筒の金額の事後期待値が x より大きいことが、 すべての x ついて成り立つ」
ことはない
と証明されています。 つまり、金額の平均値が無限大であることがパラドキシカル分布であることの条件だということです。
条件付きでない交換利得の期待値の基本
選んだ封筒に入っている金額 x が少額側の場合と高額側の場合を区別した全ての場合について交換利得と確率の積の総和をとったものを条件付きでない交換利得の期待値と呼ぶことにすると、次のようになります。金額の平均値が有限の場合の条件付きでない交換利得の期待値
金額の平均値が有限の場合には計算によってゼロとなります。また、交換して手に入る金額の平均値から交換しないで手に入る金額の平均値を引いた値のゼロとも一致します。
交換して手に入る金額の平均値から交換しないで手に入る金額の平均値を引いた値がゼロであることについてはついて、「封筒を開ける前に交換型」の場合、金額の平均値が有限の場合に封筒を交換しても期待値に変わりがないことで計算してみました。
金額の平均値が無限大の場合の条件付きでない交換利得の期待値
交換して手に入る金額の平均値から交換しないで手に入る金額の平均値を引いたものが 「条件付きでない交換利得の期待値」 に一致することを期待しつつ計算を試みると、 金額の平均値が無限大の場合、金額分布が離散的な場合に、「条件付きでない交換利得の期待値」 として選んだ封筒に入っている金額 x が少額側の場合と高額側の場合を区別した全ての場合について交換利得と確率の積の総和を計算するための数列の和の式を立てると、数列の和の項のグルーピングを変えると和の値が変わるという現象が起きます。
それに関連して、Norton, J.D. 1998. に非常に面白い発見が書かれているので Jhon D. Norton の論文に見る数列の和の項のグルーピング問題でご紹介します。
条件付き交換利得の期待値と条件付きでない交換利得の期待値の関係
金額の平均値が有限な場合
金額の平均値が有限の場合、選んだ封筒の金額を条件とする交換利得の期待値の平均は選んだ封筒の金額を条件としない交換利得の期待値と一致します。その理由について、付録の 金額の平均値が有限のとき交換利得の条件付き期待値の期待値は交換利得の期待値か で考えてみました。
このことから、「封筒を開けてから交換型」のゲームを反復した場合の 「条件付き交換利得の期待値の平均」 が、 「封筒を開ける前に交換型」のゲームにおける 「条件付きでない交換利得の期待値」 に近づいていくことがわかります。
金額の平均値が無限大の場合
Norton, J.D. 1998. に出て来るパラドキシカル分布 では 「条件付きでない交換利得の期待値」 は不定であり、 「条件付き交換利得の期待値の平均」 は無限大なので、両者の間の関係を論じることはできません。ゲームを反復したとき
2014/01/16 にこの項を加えました。- ゲームを反復したときの、選ばなかった方の封筒の金額の総額から選んだ封筒の金額の総額を引いてゲーム回数 n で割った値を平均交換利得と呼ぶことにします。
- ゲームを反復したときの、選ばなかった方の封筒の金額の総額を選んだ封筒の金額の総額で割った値を平均交換倍率と呼ぶことにします。
金額の平均値が有限な場合
この問題を論じた論文を見たことがないので自信ありませんが、ゲーム回数 n を増やすと平均交換利得がゼロに近づき、平均交換倍率が 1 に近づくでしょう。金額の平均値が無限大の場合
2014/01/17 に表題の誤りを訂正し、内容の一部も訂正しました。ゲーム回数 n を増やしても平均交換利得がゼロに近かないどころか、ますます幅が広がって行くことがあることが、Norton, J.D. 1998. を読むとわかります。
ゲーム回数 n を増やすと平均交換倍率について書かれた論文を見たことがありませんが 1 に近づかも知れないと思います。しかし大数の法則も成立しなそうなので、近づかないかも知れません。
「封筒を開ける前に交換型」の二封筒問題の数学
「封筒を開ける前に交換型」の二封筒問題で、封筒を交換した方が有利だなどということはあり得ません。 つまり、わざわざ数学で証明すべき問題ではありません。しかし! 「パラドックス」と呼ばれるほど不思議なため、証明したがる人が少なくありません。
かく言う私もその一人です。
封筒を交換しても意味がないことを数学的に証明する方法は、確率分布に差異がないことを示す方法と、期待値に差異がないことを示す方法があります。
2013/12/31 に以降の構成を整頓しました。
確率分布が同一であることを利用する方法
期待値に差異がないことを示す方法は、金額の平均値が ∞ の場合に役に立たないので、前者の方法で封筒を交換しても意味がないことを示して見ました。2013/09/22 に下記の一部を訂正しました。
- x を負でない実数とする。
- 金額のペア ( x, 2x ) を表す確率変数を P とする。
- 選んだ封筒に入っている金額の確率変数を Y とし、その具体的な値を y とする。
- Y の Y = y における確率密度は
P = (y, 2y) の確率密度とP = (y/2, y) の確率密度を足して2で割ったものである。 - 選ばなかった封筒に入っている金額の確率変数を Z とし、その具体的な値を z とする。
Z の Z = z における確率密度は P = (z/2, z) の確率密度とP = ( z, 2z ) の確率密度を足して2で割ったものである。- ゆえに、Y と Z の確率分布が同一であることがわかったので、封筒を交換しても意味がないことが証明された。
2013/11/17 に次の行を追加しました。
その後しばらくたってから、この証明や類似の証明を根拠に二封筒問題のパラドックスが解決されたと主張する人が多いことに気づきました。
そういう人たちにとっては「定義」ではなく、あくまでも「証明」なのでしょう。
条件付きでない交換利得の期待値を利用する方法
「条件付きでない交換利得の期待値の基本」 で述べたように、金額の平均値が有限な場合には、「条件付きでない交換利得の期待値」 がゼロとなるので、開ける前には二つの封筒が互角であることがわかります。金額の平均値が無限大の場合には、Norton, J.D. 1998. に書かれているように、 「条件付きでない交換利得の期待値」 を計算する式の値が定まらないので、「期待値」は開ける前の二つの封筒の互角性を判断する基準にできなそうです。
「期待値」あるいはその他の方法によって平均値無限大の二つの封筒の優劣の有り無しを説明する方法を探る研究が色々されていますが、まだ未解決の問題のようです。
Norton, J.D. 1998.
Clark, Michael. & Shackel, Nicholas. (2000).
Chalmers, David J. (2002).
余談
効用の平均値無限大の世界では期待値は無意味だということを、数学者や意思決定論者が認めれば済んでしまう問題かも知れません。
「封筒を開けてから交換型」の二封筒問題の数学
金額の確率分布の具体例を考えると、兄弟それぞれに同時に「封筒を交換した方が有利であるという状況が発生」することが珍しくないことがわかります。例として、金額ペアの確率分布が次のようだとします。
|
|
|
|---|---|
| (1, 2) | 1/3 |
| (2, 4) | 1/3 |
| (4, 8) | 1/3 |
このような確率分布で「封筒を開けてから交換型」の二封筒問題を考えると、小額側ペアの事後オッズと高額側ペアの事後オッズが等しくても、交換した方が有利になります。
たとえば、兄弟の片方の金額が 2 で、他方の金額が 4 なら、それぞれの立場に立って考えると、両者とも交換した方が有利になります。
|
|
|
|
|---|---|---|
| (1, 2) | 1/3 | 0 |
| (2, 4) | 1/3 | 1/3 |
| (4, 8) | 0 | 1/3 |
これを不思議に感じる気持ちの方こそ不思議なのです。
パラドキシカル分布の謎
「封筒を開けてから交換型」の二封筒問題で パラドキシカル分布 を考えると封筒を開けたら常に封筒を交換した方が有利になります。二封筒問題のパラドキシカル分布参照
同じ確率分布で「封筒を開ける前に交換型」の二封筒問題を考えたら、こちらの方も常に交換した方がよいのではないかと思えて、封筒を開ける前には二つの封筒が互角だという確信がゆらいできます。
パラドキシカル分布の謎参照
付録
「封筒を開ける前に交換型」の場合、金額の平均値が有限の場合に封筒を交換しても期待値に変わりがないこと
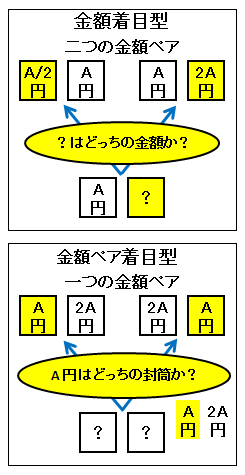
二封筒問題を解くときの考え方には次の二通りの戦略があります。ここでは、「金額着目型」の考え方で計算してみました。
離散的な場合
封筒に入る可能性のある金額を x とする。
項別の総和に分割して、
項別の総和に分割して、
よって、E=C となり、封筒を交換してもしなくても期待値が変わらないことがわかりました。
金額分布が連続的な場合
封筒に入る可能性のある金額を x とする。
項別の積分に分割して、
項別の積分に分割して、
よって、E=C となり、封筒を交換してもしなくても期待値が変わらないことがわかりました。
素事象に着目すれば話は簡単になる
上記の計算は選んだ封筒の金額に着目した「金額着目型」の議論ですが、次のような「素事象着目型」で議論するともっと簡単になります。金額分布が離散的な場合
選んだ封筒に入っている金額にそれが少額側か高額側かを組み合わせたものが素事象に対応するとします。
ある素事象について、少額側か高額側かを反転させた素事象を対事象と呼ぶことにします。
封筒を交換しない場合の期待値をEとすると
封筒を交換した場合の期待値をCとすると
上のそれぞれの式の項の間に対応関係があるので、 金額の期待値が有限の場合には
金額分布が連続的な場合
やや、ややこしいので割愛します。
金額の平均値が有限のとき交換利得の条件付き期待値の期待値は交換利得の期待値か
2013/09/25 にこの項を加えました。条件付き期待値の期待値の一般論
次のようにして、条件付き期待値の期待値は期待値に一致することを確かめました。期待値 = 全素事象の効用と確率の積の総和
条件付き期待値
条件付き期待値の期待値
よって、
二封筒問題に当てはめると
選んだ封筒に入っている金額にそれが少額側か高額側かを組み合わせたものが素事象に対応するとします。各素事象ごとに封筒を交換したときの金額の増分を効用と考え、交換利得と呼ぶことにします。
交換利得の期待値をEとすると
この式の項はある金額に関して少額側の項と高額側の項が対になっているので、 全事象を通した金額の期待値が有限の場合には、それらが打消し合うことにより、
選んだ封筒に入っている金額を証拠事象とした
全事象を通した金額の期待値が有限の場合には
パラドキシカル分布の場合にはこのようなことがないのは、いうまでもありません。
二封筒問題のパラドキシカル分布
具体例
|
|
|
|
|
期待値 |
|
|
期待値 |
|---|---|---|---|---|---|---|---|
| 1 | 少額側 | 1/6 | 1 | 0 | 1/6 | 1 |
=(1 + 1 + 2 - 4)/6 = 0 |
| 2 | 少額側 | 1/6 | -1 | 2/6 | 1/2 | ||
| 高額側 | 1/6 | 2 | |||||
| 4 | 少額側 | 1/6 | -2 | 2/6 | 1 | ||
| 高額側 | 1/6 | 4 | |||||
| 8 | 高額側 | 1/6 | -4 | 1/6 | -4 |
金額の上限を無くしても 同確率条件 は成立しなそうだ
簡単にするため、離散的なケースを考えます。選んだ封筒に x という金額が入っていたとします。そうすると、もしも同確率条件が成立するならば、
(2nx, 2n+1x) のペアのうち、2nx の方に同確率条件が成立するとすると
ということはこうして出来た全ての金額ペアが同確率で発生することになるので、 それらの確率の総和が無限大に発散します。
ゆえに全ての金額ペアの確率の総和も無限大に発散します。
ゆえに、離散的な金額分布の場合には同確率条件は成立しません。
次に金額分布が連続で確率密度関数も連続な場合を考えてみました。
金額ペア (x, 2x) の確率密度関数を g(x) とすると
少額側の金額 s 単独の確率密度関数は g(s) で、
高額側の金額 k 単独の確率密度関数は g(k/2)/2 。
よって、同確率条件から、2g(x) = g(x/2)。 (※1)
よって
この関数を積分すると無限大になってしまいます。
ゆえに、連続的な金額分布の場合にも同確率条件は成立しません。
※1 Chalmers, D.J. 1994. にも同じ式が出て来ます。Chalmers の論文
※2 g(x) = a / x という式が必ず導かれるか余り自信ありませんが、一つの例ではあるし、 統計学博士の美添泰人さんのホームページからリンクされている 「確率に関するパラドックス(その1)」 という表題の pdf ファイルでも同じ関数が導かれているので、間違いないでしょう。
金額分布が連続的な場合の計算にあやふやなところがありますが、同確率条件が成立しなそうだという気にはなります。
この問題に関する論文を調べれば、もしかしたら同確率条件が成立する確率分布が発見されているかも知れませんが、それもなさそうな話です。
もしそうなら色々な論文で紹介しているだろうからです。
参考文献
-
Broome,John.(1995).
The Two-envelope Paradox, Analysis 55(1): 6-11.
-
Chalmers, D.J. 1994.
The two-envelope paradox: A complete analysis?
-
Chalmers, David J. (2002).
The St. Petersburg Two-Envelope Paradox. Analysis 62 (2): 155–157.
-
Clark, Michael. & Shackel, Nicholas. (2000).
The Two Envelope Paradox, Mind Magazine (Vol 109.435.July 2000)
-
Norton, J.D. 1998.
When the sum of our expectations fails us: The exchange paradox.
Pacific Philosophical Quarterly 79:34–58.
用語解説
-
同確率条件
私の造語です。
封筒を交換したときに金額が倍増する確率と半減する確率がともに1/2 であることが、
最初に選らんだ封筒の金額によらず常に成立することを言います。
-
パラドキシカル分布
選んだ封筒の金額を条件とする条件付き期待交換利得が常にゼロより大であるような金額分布を言います。
トップページに戻る