トップページに戻る
なるべく多くの人に二つの封筒問題をわかってもらうため、他の人の書いたページも紹介するなど、あの手この手で説明します。
e = (確率1/2) (x/2) + (確率1/2) 2x = 1.25x
x/2 と x の組み合わせから x を選ぶ確率(= 1/2)
x と 2x の組み合わせから x を選ぶ確率(= 1/2)
もう一つの封筒の金額が x/2 だということは、x/2 と x で二つの封筒が構成されていることを意味していて、 もう一つの封筒の金額が 2x だということは、x と 2x で二つの封筒が構成されていることを意味しているのだから、 実際には、次の確率も考えに入れなければいけなかったのです。
封筒の中身が x/2 と x の組み合わせである確率
封筒の中身が x と 2x の組み合わせである確率
これを踏まえて、期待値計算式を書き直すと次のようになります。
選んだ封筒に x が入っていたときにx/2 と x の組み合わせである確率を P(x/2とx | x入) と書き、 x が入っていたときに x と 2x の組み合わせである確率を P(xと2x | x入) と書くことにすると、
e =P(x/2とx | x入) (x/2) + P(xと2x | x入) 2x
= ( (1/2) P(x/2とx | x入) + 2 P(xと2x | x入) ) x
結局、交換した方がよいかどうかは、期待値計算式を考えてもわからないので、心配することはなかったのです。
· · · といった具合に論理的に説明されただけでは安心できない人もいます。 私のその一人です。
そういう人のために直観的に理解できるような図解を試みました。
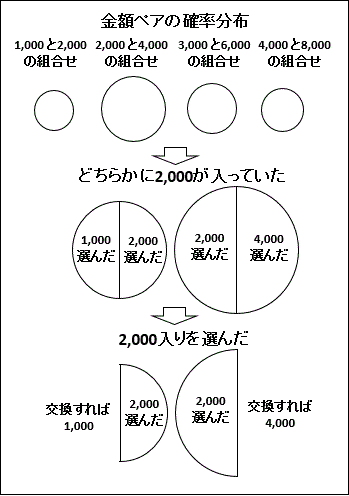
2017年6月に英語のページ "An outline of the Two Envelopes Problem" 用に作った次の図もわかりやすいかも知れません。
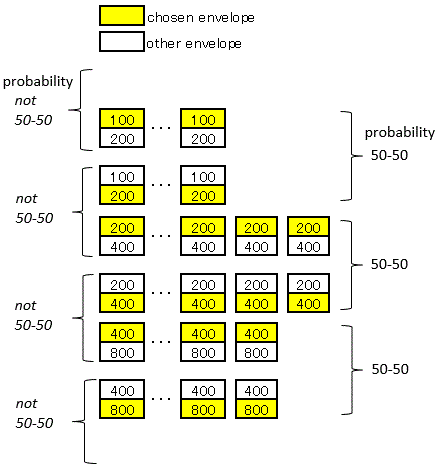
(↑ 2017/06/24 追加)
このことをもっと理解したい人には、次のページがわかりやすいと思います。
二つの封筒問題からパラドックスを発生させるためには、金額の確率分布が次のような条件を持たなければなりません。
たとえば、もしも1円が可能であるなら、たとえ 現象 としてあり得なくても 0.5円も 事象 として考えなければならないし、もしも一兆の一兆倍の金額が可能であるなら、一兆の2兆倍の金額も 事象 として考えなければなりません。 そうでなければ期待値計算式の二つの項の一つが意味を持たなかったり値が不定になったりするため、 期待値計算式が意味を持てず、 パラドックスと無縁になってしまいます。
このようなことから、二つの封筒問題を数学的に議論するときは、正の実数の集合で考えたり、有理数による2のべき(の定数倍)の集合で考えたりすることが一般的です。
「…常に上回るような確率分布はない」 ということについては Broome,John.(1995). などの論文で証明されています。
「…常に 1/2 であるような確率分布はない」 ことについては、次のページの説明がわかりやすいと思います。
次の例はそうした確率分布の中で最も有名で、色々なWebページで紹介されています。
この種の確率分布だと常に交換した方が有利であることを理解するには、次のWebページが参考になります。
この謎はみなさんの楽しみのために残しておきます。
この問題にチャレンジした論文として次のものがあります。
そしてこのような人たちの中の一部は 「変数誤用説」 を唱えます。
Y の期待値 = ½ × (x/2) + ½ × 2x の最初の項の x は 2a を表し、2番目の項の x は a を表しているので、変数記号 x が誤って使われている。
別の人たちは 「二組の金額ペア妄想説」 を唱えます。
Y の期待値 = ½ × (x/2) + ½ × 2x という計算式は(x/2, x) と (x, 2x) という二組の金額ペアを考えている。
しかし、封筒を選ぶ段階では封筒の中の金額ペアは一組しかないからこのような期待値計算式を考えるのは誤りである。
同一の書き間違いの説明として、「変数誤用説」 と 「二組の金額ペア妄想説」 という相反する理論が出されているので、これらの説が両方とも妄想でしかないことが強く示唆されます。
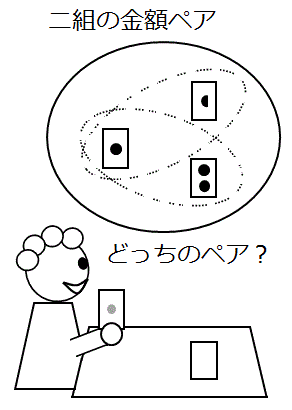
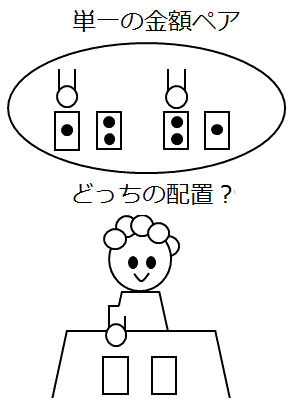
二つの封筒問題のパラドックスを楽しむためには前者のメンタルモデルで考える必要がありますが、Y の期待値 = ½ × (x/2) + ½ × 2x が正解だと考える人たちはそれを許しません。後者のメンタルモデルしか受け入れません。
「変数誤用説」 が唱えるような心理現象はあるか
彼らはなぜパラドックスの源を捨て去れるのか
「二組の金額ペア妄想説」 や 「変数誤用説」 がデマであることを証明する、あるいは逆に、人間の頭の中で実際に起きることがあることを証明する、といった心理学実験がなされるまで、悩みは続きます。
「変数誤用説」 がパラドックスの原因だとする説がどんなに奇妙であるか、当ホームページの次のページで詳しく調べてみましたが、 結局、心理学者が実験しないことには決着が付きません。
「単一金額ペア固執派」 の人が考える 「単一金額ペア型の二つの封筒問題」
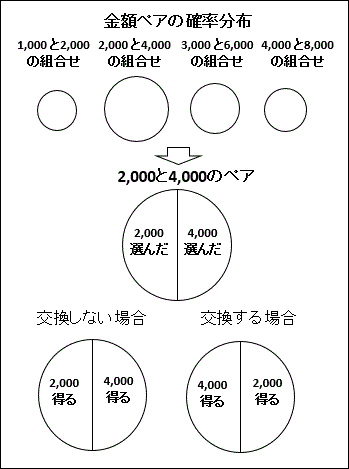
「二組金額ペア想起派」 の人が考える 「二組金額ペア型の二つの封筒問題」
(先にお見せした図と同じですが、比較のため再掲します)

「二組の金額ペア妄想説」 や 「変数誤用説」 が予想するような心理現象が人間の頭の中で実際に起きることがあると証明されたときには、 二つの異なる 「二つの封筒問題のパラドックス」 の存在が同時に証明されることになります。
「二組の金額ペア妄想説」 と 「変数誤用説」 という相反する説が存在することは次のように考えると理解できます。
「二組金額ペア型の二つの封筒問題」 は 「単一金額ペア型の二つの封筒問題」 の要素を含んでいる
「二組金額ペア型二つの封筒問題」 でも二つの封筒が同等であることを証明する過程で、 ある一組の金額ペアが封筒に入れられたときに、その金額ペアの少額側の金額の入った封筒を選ぶ確率と高額側の金額が入った封筒を選ぶ確率が半々であることを必ず利用するので、 「二組金額ペア型の二つの封筒問題」 は 「単一金額ペア型の二つの封筒問題」 の要素を含んでいることがわかります。
「二組金額ペア型の二つの封筒問題」 は 「単一金額ペア型の二つの封筒問題」 より強力である
「二組金額ペア型の二つの封筒問題」 は 「封筒を開けてから交換型」 の二つの封筒問題にも応用できるし、 「パラドキシカル分布」 を導くこともできますが、「単一金額ペア型の二つの封筒問題」 ではそのようなことができません。
improper な確率分布も限定的になら考えてよいとする統計数学者もいるので、このような場合はどうなのか、考えたくなります。 しかし、次のようにあっさりとパラドックスが解消してしまいます。
当ホームページの次のページも参考になるかも知れません。
Cover 博士のアイデア (Cover,T.M.(1987)) などを 「封筒を開けてから交換型」 のゲームに応用して、なるべくたくさん儲ける戦略を研究している人もいます。 私は読んだことがありませんが、 Wikipedia(英語版) の "Two Envelopes problem" の記事に次の例が載っていました。
期待値計算式を含まない二つの封筒問題を考えることができます。
「封筒を開ける前に交換型」 の場合には、このように期待値計算式を含まない問題文にすると、確率の錯覚よりも交換で減ったり増えたりするときの金額に関する錯覚の方が起きやすそうな気がします。
確率の錯覚で片付かないので普通の問題文より面白そうですが、このような問題文での議論を見たことがありません。
トップページに戻る
2017/06/24 22:42:38
初版 2014/05/20
 多くの人がわかる · · · かもしれない二つの封筒問題
多くの人がわかる · · · かもしれない二つの封筒問題
なるべく多くの人に二つの封筒問題をわかってもらうため、他の人の書いたページも紹介するなど、あの手この手で説明します。
二つの封筒問題のおさらい
「封筒を開ける前に交換型」の二封筒問題とは次のようなものです。- お金もしくは小切手の入った二つの封筒があり、一方には他方の倍の金額が入っている。
- どちらが大きな金額か知らないでランダムに封筒を選ぶと中身がもらえる。
- 選らんだ封筒の中身を x とすると、もう片方の中身は
確率 1/2 で x/2、確率 1/2 で 2x だ。 - だから選ばなかった方の金額の期待値は
(1/2)(x/2) + (1/2)2X = 1.25x で x より大きい。 - 選ばなかった方の金額の期待値の方が大きいから封筒を替えさせてもらおう。
- その後で同じことを考えるので永久に封筒を替え続けることになってしまう???
- 不思議だ。
- お金もしくは小切手の入った二つの封筒があり、一方には他方の倍の金額が入っている。
- どちらが大きな金額か知らない二人の兄弟がランダムに別々の封筒を選ぶ。
- 二人は相手に分からないようにして封筒の中身を見る。
- 兄弟の一人の封筒の中身は x だったので、次のように考えた。
- もう一人の封筒の中身は
確率 1/2 で x/2、確率 1/2 で 2x だ。 - だからもう一人の封筒の金額の期待値は
(1/2)(x/2) + (1/2)2X = 1.25x で x より大きい。 - もう一人の封筒の金額の期待値の方が大きいから封筒を交換することを提案しよう。
- 兄弟ともに同じことを考える???
- 不思議だ。
パラドックスの元となる期待値計算式
「封筒を開ける前に交換型」 でも、「封筒を開けてから交換型」 でも、パラドックスの源は期待値計算式です。最初に選んだ封筒の金額 x に対して選ばなかった方の封筒の金額の期待値を次のような式で計算したために、謎が発生しています。確率の錯覚がパラドックスの原因
上記の期待値計算式の中の 1/2 という確率の値が間違っていたのです。 次の二つの確率しか考えていないために、このような錯覚をしてしまったのです。x/2 と x の組み合わせから x を選ぶ確率
x と 2x の組み合わせから x を選ぶ確率
もう一つの封筒の金額が x/2 だということは、x/2 と x で二つの封筒が構成されていることを意味していて、 もう一つの封筒の金額が 2x だということは、x と 2x で二つの封筒が構成されていることを意味しているのだから、 実際には、次の確率も考えに入れなければいけなかったのです。
封筒の中身が x/2 と x の組み合わせである確率
封筒の中身が x と 2x の組み合わせである確率
これを踏まえて、期待値計算式を書き直すと次のようになります。
選んだ封筒に x が入っていたときに
結局、交換した方がよいかどうかは、期待値計算式を考えてもわからないので、心配することはなかったのです。
· · · といった具合に論理的に説明されただけでは安心できない人もいます。 私のその一人です。
そういう人のために直観的に理解できるような図解を試みました。
2017年6月に英語のページ "An outline of the Two Envelopes Problem" 用に作った次の図もわかりやすいかも知れません。
(↑ 2017/06/24 追加)
このことをもっと理解したい人には、次のページがわかりやすいと思います。
- kojette さんのブログサイト "kojetteの研磨日記" の 「一連の確率問題の解説 via 「2つの封筒問題」続き」 というページ
パラドックス発生のための条件
2015/02/15 にこの項を加えました。二つの封筒問題からパラドックスを発生させるためには、金額の確率分布が次のような条件を持たなければなりません。
二つの封筒問題で 現象 として発生する可能性のある金額すべてについて、その半分と倍の金額も 事象 として考えなければならない。
たとえば、もしも1円が可能であるなら、たとえ 現象 としてあり得なくても 0.5円も 事象 として考えなければならないし、もしも一兆の一兆倍の金額が可能であるなら、一兆の2兆倍の金額も 事象 として考えなければなりません。 そうでなければ期待値計算式の二つの項の一つが意味を持たなかったり値が不定になったりするため、 期待値計算式が意味を持てず、 パラドックスと無縁になってしまいます。
このようなことから、二つの封筒問題を数学的に議論するときは、正の実数の集合で考えたり、有理数による2のべき(の定数倍)の集合で考えたりすることが一般的です。
数学的に安心したい人のために
二つの封筒に入る可能性のある金額の組み合わせの確率分布を考えた場合、封筒の中に入っている金額の平均値が有限の場合には、- もう一つの封筒の金額の選んだ封筒の金額を条件とする期待値が選んだ封筒の金額を常に上回るような確率分布はない。
- 選んだ封筒の金額が x のときにもう片方がx/2の確率ともう片方が2xである確率が、 x の値によらず常に 1/2 であるような確率分布はない。
- 選んだ封筒の金額によって交換した方がよかったり、しない方がよかったりしても、選んだ封筒に入っている可能性のある金額全体で考えたときに、常に交換した場合と常に交換しない場合とで差はない。 ( ← 2014/11/04 に加筆)
「…常に上回るような確率分布はない」 ということについては Broome,John.(1995). などの論文で証明されています。
「…常に 1/2 であるような確率分布はない」 ことについては、次のページの説明がわかりやすいと思います。
- tazuma さんのブログ 「Essay, dated.」の「 2つの封筒のパラドックスの変形問題 その2 - Essay, dated.」 というページ
Cover博士が提起した問題がすっきりした数式で説明されていて、さらにその応用として、「他の封筒が大きいあるいは小さい金額を含む確率が常に半々だということはありえない」 ことが書かれています。
- イギリスのBBCの
「BBC - h2g2 - The Two-envelope Paradox」 というページ
最後の方の"A Demonstration" という段落に、常に交換したときの損得の表があって、それらの総和がゼロだから常に交換したときとしないときで差がないことを示しています。
数学的に楽しみたい人のために
金額の平均値が無限大の場合、つまり宇宙より大きな小切手、宇宙より大きな封筒、それを受け取る宇宙より大きな手があった場合、金額ペアの確率分布によっては、選んだ封筒の金額を条件とするもう一つの封筒の金額の期待値が選んだ封筒の金額を常に上回ることがあります。 (2014/09/23 にこの文章の曖昧なところを修正しました)次の例はそうした確率分布の中で最も有名で、色々なWebページで紹介されています。
| 金額ペア | 確率 |
|---|---|
|
|
|
|
|
|
| 途中省略 | 途中省略 |
|
|
|
| 以下同様 | 以下同様 |
この種の確率分布だと常に交換した方が有利であることを理解するには、次のWebページが参考になります。
- tasusu さんの「むしゃくしゃしてやった、今は反省している日記」 というブログの 「たのしい確率 ~2つの封筒問題~」 という記事
パラドキシカルな金額分布の例についての、封筒を交換したときの利得の期待値が常に正であることの説明が、実にすっきりとしています。
封筒を選んでから開けるまでの間を考えると、まだ開けていないので二つの封筒は同等のように思える。
しかし、選んだ封筒の中にはまだ開けていないとは言え、確定した金額が入っているので、封筒を交換した方が有利になる。
不思議だ。
しかし、選んだ封筒の中にはまだ開けていないとは言え、確定した金額が入っているので、封筒を交換した方が有利になる。
不思議だ。
この謎はみなさんの楽しみのために残しておきます。
この問題にチャレンジした論文として次のものがあります。
心理学的に悩みたい人のために
2015/9/5 にこの項を全面的に書き換えました。単一の金額ペアで考えた期待値計算式を正解だと勘違いする人たち
世の中には次のように考える人がいます。|
二つの封筒の金額ペアを (a, 2a) とし、
選んだ封筒ともう一方の封筒の金額の確率変数をそれぞれ X, Y とすると、 ↓ パラドックスが解消した。 ↓ パラドックスの元となった計算式、 書き間違いだったのだ。 |
そしてこのような人たちの中の一部は 「変数誤用説」 を唱えます。
別の人たちは 「二組の金額ペア妄想説」 を唱えます。
しかし、封筒を選ぶ段階では封筒の中の金額ペアは一組しかないからこのような期待値計算式を考えるのは誤りである。
同一の書き間違いの説明として、「変数誤用説」 と 「二組の金額ペア妄想説」 という相反する理論が出されているので、これらの説が両方とも妄想でしかないことが強く示唆されます。
単一の金額ペアで考えた期待値計算式を正解だと勘違いする人たちの頭の中
二つの封筒問題を考えるとき次のような二つのメンタルモデル(頭の中の図式)で考えることができます。二つの封筒問題のパラドックスを楽しむためには前者のメンタルモデルで考える必要がありますが、
心理学的な問題
「二組の金額ペア妄想説」 が唱えるような心理現象はあるか
(x/2, x) と (x, 2x) という二組の金額ペアを使って期待値計算式を作り、パラドックスを感じ、そしてその後で
「二組の金額など思ってもよらない。どうして二組の金額を考えてしまったのだろう?」
などと驚くような人が実際にいるのか?
「二組の金額など思ってもよらない。どうして二組の金額を考えてしまったのだろう?」
などと驚くような人が実際にいるのか?
「変数誤用説」 が唱えるような心理現象はあるか
a を x/2 と書き、2a を 2x と書いて期待値計算式を作り、パラドックスを感じ、そしてその後で変数記号を誤って使っていたことに気づいて驚くような人が実際にいるのか?
たとえ変数記号を誤って使ったとしても、計算結果が怪しいとわかった時点で気が付くのではないのか?
たとえ変数記号を誤って使ったとしても、計算結果が怪しいとわかった時点で気が付くのではないのか?
彼らはなぜパラドックスの源を捨て去れるのか
二組の金額ペアを考えたればこそパラドックスを楽しめることに 「二組の金額ペア妄想説」 や 「変数誤用説」 を唱える人はなぜ気づかないのか?
彼ら自身がパラドックスを感じていないがゆえに、パラドックスの源を捨て去って平気でいられるのではないか?
彼ら自身がパラドックスを感じていないがゆえに、パラドックスの源を捨て去って平気でいられるのではないか?
「二組の金額ペア妄想説」 や 「変数誤用説」 がデマであることを証明する、あるいは逆に、人間の頭の中で実際に起きることがあることを証明する、といった心理学実験がなされるまで、悩みは続きます。
「変数誤用説」 がパラドックスの原因だとする説がどんなに奇妙であるか、当ホームページの次のページで詳しく調べてみましたが、 結局、心理学者が実験しないことには決着が付きません。
二つの 「二つの封筒問題」
「二組の金額ペア妄想説」 や 「変数誤用説」 を唱える 「単一金額ペア固執派」 の人が考える 「二つの封筒問題」 と、このような説を唱えない 「二組金額ペア想起派」 の人の考える 「二つの封筒問題」 とでは、 期待値を計算するときの条件が全く異なるので、 数学的にまったく別の問題です。「単一金額ペア固執派」 の人が考える 「単一金額ペア型の二つの封筒問題」
「二組金額ペア想起派」 の人が考える 「二組金額ペア型の二つの封筒問題」
(先にお見せした図と同じですが、比較のため再掲します)
「二組の金額ペア妄想説」 や 「変数誤用説」 が予想するような心理現象が人間の頭の中で実際に起きることがあると証明されたときには、 二つの異なる 「二つの封筒問題のパラドックス」 の存在が同時に証明されることになります。
「二組の金額ペア妄想説」 と 「変数誤用説」 の関係
2014/11/11 に書いた項 「単一金額ペアへの固執」 を起こしつつも 「変数誤用説」 を唱えない人たち」 を 2015/9/5 にこの項で置き換えました。「二組の金額ペア妄想説」 と 「変数誤用説」 という相反する説が存在することは次のように考えると理解できます。
- なんらかの理由で
Y の期待値 = ½ × (x/2) + ½ × 2x はY の期待値 = ½ × a + ½ × 2a の書き間違いだと勘違いした。 - この説を正当化するために、書き間違いが発生する原因を想像した。
- ある人は 「二組の金額ペア妄想説」 を唱え、別の人は 「変数誤用説」 を唱えた。
二つの 「二つの封筒問題」 の数学的関係
「単一金額ペア固執派」 の人が考える 「単一金額ペア型の二つの封筒問題」 と 「二組金額ペア想起派」 の人の考える 「二組金額ペア型の二つの封筒問題」 の間に次のような関係があります。「二組金額ペア型の二つの封筒問題」 は 「単一金額ペア型の二つの封筒問題」 の要素を含んでいる
「二組金額ペア型二つの封筒問題」 でも二つの封筒が同等であることを証明する過程で、 ある一組の金額ペアが封筒に入れられたときに、その金額ペアの少額側の金額の入った封筒を選ぶ確率と高額側の金額が入った封筒を選ぶ確率が半々であることを必ず利用するので、 「二組金額ペア型の二つの封筒問題」 は 「単一金額ペア型の二つの封筒問題」 の要素を含んでいることがわかります。
「二組金額ペア型の二つの封筒問題」 は 「単一金額ペア型の二つの封筒問題」 より強力である
「二組金額ペア型の二つの封筒問題」 は 「封筒を開けてから交換型」 の二つの封筒問題にも応用できるし、 「パラドキシカル分布」 を導くこともできますが、「単一金額ペア型の二つの封筒問題」 ではそのようなことができません。
improper な確率分布について
封筒を交換すると半々の確率で半減したり倍増したりする確率分布は全事象の確率の総和が 無限大なので、確率の総和が 1 でない improper な確率分布だということになります。improper な確率分布も限定的になら考えてよいとする統計数学者もいるので、このような場合はどうなのか、考えたくなります。 しかし、次のようにあっさりとパラドックスが解消してしまいます。
確率の総和が無限大な確率分布を許した場合、常に交換した方が有利な確率分布が存在する。
しかし、確率の総和が無限大の場合、平均値も無限大となる。
そうすると平均値を二つの封筒の互角性の根拠にすることができないため、対称性だけが根拠として残る。
常に交換した方が有利だということは対称性と矛盾しない。(お互いさまだから)
よって常に交換した方が有利であることと二つの封筒が互角であることは矛盾しない。
しかし、確率の総和が無限大の場合、平均値も無限大となる。
そうすると平均値を二つの封筒の互角性の根拠にすることができないため、対称性だけが根拠として残る。
常に交換した方が有利だということは対称性と矛盾しない。(お互いさまだから)
よって常に交換した方が有利であることと二つの封筒が互角であることは矛盾しない。
人の説に惑わされないために
Yahoo! 知恵袋などのQAサイトの回答を読むと、びっくりするほど様々な説があります。それらを読んで事前に様々な説があることを知っておけば、知ったかぶりをする人の珍説に惑わされないですむでしょう。当ホームページの次のページも参考になるかも知れません。
ギャンブル好きの人のために
2014/09/21 にこの項を加えました。Cover 博士のアイデア (Cover,T.M.(1987)) などを 「封筒を開けてから交換型」 のゲームに応用して、なるべくたくさん儲ける戦略を研究している人もいます。 私は読んだことがありませんが、 Wikipedia(英語版) の "Two Envelopes problem" の記事に次の例が載っていました。
期待値計算式のない二つの封筒問題
2015/03/30 にこの項を加えました。期待値計算式を含まない二つの封筒問題を考えることができます。
- お金もしくは小切手の入った二つの封筒があり、一方には他方の倍の金額が入っている。
- どちらが大きな金額か知らないでランダムに封筒を選ぶと中身がもらえる。
- 封筒を交換すると確率 1/2 で手持ちの半分を失い、確率 1/2 で手持ちと同額を増やせる。
- だから平均すると交換で金額が増えるから封筒を替えさせてもらおう。
- その後で同じことを考えるので永久に封筒を替え続けることになってしまう???
- 不思議だ。
「封筒を開ける前に交換型」 の場合には、このように期待値計算式を含まない問題文にすると、確率の錯覚よりも交換で減ったり増えたりするときの金額に関する錯覚の方が起きやすそうな気がします。
確率の錯覚で片付かないので普通の問題文より面白そうですが、このような問題文での議論を見たことがありません。
参考文献
-
Broome,John.(1995).
The Two-envelope Paradox, Analysis 55(1): 6–11.
-
Cover,T.M.(1987)
Pick the largest number
In Open problems in communication and computation
(eds. T. M. Cover & B. Gopinath), p. 152. Berlin, Germany: Springer
-
McDonnell, M.D. , Grant, A.J. , Land, I. , Vellambi, B.N. , Abbott, D. And Lever, K. (2011).
Gain from the two-envelope problem via information asymmetry: on the suboptimality of randomized switching
Proceedings of the Royal Society A.
-
Norton, J.D. 1998.
When the sum of our expectations fails us: The exchange paradox.
Pacific Philosophical Quarterly 79:34–58.
用語解説
-
パラドキシカル分布
選んだ封筒の金額を条件とする条件付き期待交換利得が常にゼロより大であるような金額分布を言います。
このような場合、封筒を開ける前の二つの封筒が互角であることと矛盾しないのか? と不思議になります。
-
変数誤用説
私の造語です。
「封筒を交換した後の金額の期待値を計算する½ × (x/2) + ½ × 2x という式の左の x は交換して半減するときの値を表し、右の x は交換して倍増するときの値を表していて、同じ変数が別の値を表しているから、おかしな計算結果になるのだ」
という説を指します。
二封筒問題のおまじないの王様 – 変数誤用説 –の中核部分に当たります。
-
二組の金額ペア妄想説
「二組の金額ペア (x/2, x) (x, 2x) を考えたから、誤った期待値計算式E = (1/2)(x/2) + (1/2)2x を思いついてしまっただ。そもそも単一の金額ペア (a, 2a) で考えないからいけないのだ。」 という説です。
「変数の誤用説」 と並んで、E = (1/2)a + (1/2)2a が正しい期待値計算式だとする説の双璧をなしています。
英語でネット検索すると、「変数の誤用説」 よりもこの 「二組の金額ペア妄想説」 信奉者の方が数が多そうです。 (2015/8/29現在)
トップページに戻る