トップページに戻る
二封筒問題の錯覚現象とモンティ・ホール問題や3囚人問題との類似点を発見したことが切っ掛けでのこのページを 2012/7/29 に書きました。
その後何度も手を加えて、2013/12/28 にようやく現在の形になりました。
ニ封筒問題は Wikipedia(英語版)の "Monty Hall problem" の記事でモンティ・ホール問題に類似したパズルとして紹介されています。
Wikipedia(英語版)の "Two envelopes problem" の記事 (17::52, 17 June 2012 の版) では、二封筒問題の問題文として、次のような問題文を採用しています。
このパズルは、結論が誤りであることが自明でありながら、論理のどこで勘違いしているのか簡単には分からず、ついつい、金額の確率分布から封筒を替えたときの期待値を統計数学で求めようとして、ますます混乱して来るという特徴があります。
実際は、このパズルで言うようなことは絶対にないので、統計数学を持ち出すまでもない問題ですが、そのことに自信が持てないため、「パラドックス」と呼ぶ人もいます。
結論が誤りであることが自明であるという点で自転車のパズルと似ていますが、自転車のパズルは小学生レベルの問題で、二封筒問題は大学生レベルの問題だといえそうです。 (自転車のパズルについては、モンティ・ホール問題と自転車のパズルとの共通点 でとりあげました。)
「封筒を開ける前に交換型」の二封筒問題とモンティ・ホール問題の類似点については、 封筒を開ける前に交換型の二封筒問題独自の錯覚現象 で考えました。
封筒を開けてから交換型のニ封筒問題は Wikipedia(英語版)の "Two envelopes problem" の記事の初版によると次のような問題です。
注:不思議なことにWikipedia(英語版)の "Two envelopes problem" の記事の問題文が2005年ごろに封筒を開ける前に交換型の二封筒問題にすり替わっています。
Wikipedia(英語版)の "Two envelopes problem" で二封筒問題を知った私には意外でしたが、日本語でインターネット検索すると「封筒を開けてから交換型」の二封筒問題の方が多く出て来ます。
このような形式の場合、最初に選んだ封筒の金額を証拠事象とした上で、その封筒が高額側である条件付き確率や少額側である条件付き確率を考える問題になります。
そして、どちらの封筒を選んでも交換した方が有利であるような金額が封筒に入ることがあるような確率分布を考えることは簡単です。 (そのかわり、開ける前に交換するタイプとちがって、一回交換したら後もどりできません)
開けた封筒の中の金額によらず常に封筒を交換した方がよいような確率分布すらあります。 (そのような確率分布を工夫した例を、 二封筒問題のパラドキシカル分布 でとりあげました。)
「封筒を開けてから交換型」の二封筒問題とモンティ・ホール問題の類似点については、 封筒を開けてから交換型の二封筒問題はモンティ・ホール問題にもっと似ている で考えました。
2013/09/13 に以下を書き加えました。
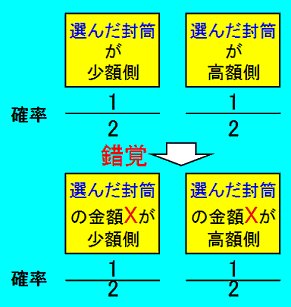
それは、封筒にだけ着目したときの大小関係と封筒の中身の金額も考慮した大小関係を同一視している点です。
そのため次のような錯覚が生じます。
あなたが選んだ封筒に A 円入っていたとすると、封筒を切り替えて手に入る金額の期待値が 1.25A円に思えてしまいます。
ところがこの計算式には 怪しい点があります。
封筒の中の金額 A の値に無関係に、切り替えて半分になる確率や倍になる確率がどちらも1/2 だとしている点です。
実際に上記の数式が成立するためには次の条件が必要です。
要は、手持ちの封筒に対して、 封筒を切り替えて金額が倍になる確率と半分になる確率がどちらも1/2 だということから、
手持ちの封筒の中の金額 A に対してもそうだと勘違いしたために、 このような錯覚に陥るのです。
実際には、金額Aの入っている封筒が少額側の封筒である確率と、高額側の封筒である確率も考慮する必要があったのです。
交換によって倍になる金額の確率分布と、交換によって半分になる金額の確率分布の例によって、このことを示すことができます。
封筒に着目したときの確率が封筒の中の金額に着目したときの確率と一致するとは限らないことを、 Wagner, Carl G.(1999). を参考にしながら、数式で表現すると次のようになります。 (2014/05/12 にこの部分を書き加えました)
しかし、それでもなお、同確率条件は決して成り立たないと思います。 (別ページ 二封筒問題の数学 の付録で論じています)
金額に上限を付けず、金額の平均値も無限大を許すのであれば、選んだ封筒の金額が決まった後には常に封筒を交換した方が有利な金額分布があります。そのような金額分布をパラドキシカル分布( 二封筒問題のパラドキシカル分布) と呼びますが、パラドキシカル分布でも最低金額を選んだときを除いて全域にわたって封筒を交換すると半分になりやすく、同確率条件は成立していません。
連続的な金額分布の場合はどうかというと、Chalmers, D.J. (1994).に簡単な方法が示されています。
g(x) = 1/x という関数を確率密度関数の材料にして、 金額の上限下限を設定し、適当な係数を掛けて確率密度の積分が1になるようにする方法です。 (別ページ 「Chalmers の論文」 でも解説しています)
しかし倍率は量でないので、平均値の1.25 は、倍率計算の分母が同じでなければ、期待値の代わりになりません。
こういう中途半端な意味を 1.25 が持っていることが錯覚の元になっているのかも知れません。
確率の錯覚の数学的構造はマンモグラフィの確率の錯覚の数学的構造に近いことに最近(2013年11~12月ごろ)に気づきました。 二封筒問題共通の錯覚現象とマンモグラフィの錯覚との類似点
ニ封筒問題に上記のような惑わしポイントが生じるのは、問題を考えるときのメンタルモデルが不適切なためだとも考えられます。
ニ封筒問題を読んだときに思い浮かべるであろうメンタルモデルは下記の 「ニ封筒問題で錯覚を起こすメンタルモデル」 であろうと思います。
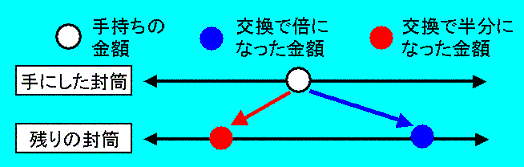
このような不適切なメンタルモデルだから、封筒を切り替えると賞金が倍になる確率と半分になる確率が 手にした封筒の金額 によらず常に1/2 だと錯覚してしまうのです。
適切なメンタルモデルの方を思い浮かべれば、賞金が 2倍になる金額の分布と、半分になる金額の分布に違いがあることがすぐにわかります。
二封筒問題の
錯覚を起こす
適切な
二封筒問題の
2013/09/20 に下図を加えました。
錯覚を起こす
適切な
金額分布が連続な場合はやや複雑なので割愛します。
適切な
2013/09/26 にこの図を加えました。
金額分布が連続な場合はやや複雑なので割愛します。
適切な
2013/12/21 にこの図を加えました。
金額分布が連続な場合はやや複雑なので割愛します。
参考:モンティ・ホール問題の
モンティ・ホール問題で錯覚を起こす
モンティ・ホール問題で錯覚を起こさない適切な
このように、「不適切なメンタルモデルによる錯覚現象」 という点で、二封筒錯覚とモンティ・ホール問題に共通するものがあります。
この二つの戦略が頭の中で混ざり合うために、上で見たような不適切なメンタルモデルが出来上るのかも知れません。
実際、金額ペア着目型で考えるならあくまでも金額ペア着目型で貫き通し、金額着目型で考えるならあくまでも金額着目型で貫き通せば、混乱はなくなります。
「封筒を開ける前に交換型」の二封筒問題であれば金額ペア着目型で考えると、封筒を替えても替えなくても同じであることを示すことができます。
封筒を開ける前なら封筒を替えても替えなくても同じであることの金額ペア着目型説明
モンティ・ホール問題にこの理論を適用すると次のようになります。
「封筒を開けてから交換型」の二封筒問題でも、「封筒を開ける前に交換型」の二封筒問題でも、選んだ封筒の金額を特定した上で、その封筒が少額側であるときにその金額である確率の計算式の中で、その封筒が 「その金額ペア」 である確率、すなわち「基準率」 が重要な位置を占めています。 (二封筒問題共通の錯覚現象とマンモグラフィの錯覚との類似点 で詳しく見ています)
このことから、二封筒問題の確率の錯覚は 「基準率錯誤」 の一種であるので、錯覚の数学的構造の面ではマンモグラフィーの錯覚の方に近いと言えます。
条件付確率の問題設定
不特定事象による条件付確率の問題設定
非条件付確率の問題設定
これらの問題設定の違いは条件付き確率を考えるときの証拠事象の範囲の違いです。
一方、二封筒問題の場合は、「封筒を開ける前に交換型」と「封筒を開けてから交換型」の2タイプで次のように証拠事象の範囲が違っています。
この点は、モンティ・ホール問題と二封筒問題の類似点の一つでもありますが、二封筒問題の場合、証拠事象の範囲の違いがゲームのルールの違いと対応している点が、モンティ・ホール問題の場合と大きく異なります。
二封筒問題とモンティ・ホール問題との間に、「確率の錯覚現象」 という共通点がありますが、数学的に理解した後の不思議さという点ではマンモグラフィーの確率の錯覚現象に近いように思います。
こういう考え方をすると金額の確率分布など関係なくなってしまい、少額の金額と高額の金額の2種類の金額に関する単純な問題になります。
2013/09/26 にこの箇所を修正しました。
やや複雑ですが、金額着目型の場合も、封筒を開ける前なら封筒を替えても替えなくても同じであることを示すことができます。 (二封筒問題の数学)
金額ペア固定型の親戚の金額ペア横断型の考え方で、二つの封筒の金額の総和を固定しないで計算することもできます。
金額が離散的な場合で説明します。
金額ペアを (sn, bn) で表す。
その金額ペアの出現確率を Pn とする。
選んだ封筒に入っている金額の期待値を E とする。
E = 下記の項の全ての和。
(1/2)×Pn×sn
・・・・・少額側の項
(1/2)×Pn×bn
・・・・・高額側の項
交換した先の封筒に入っている金額の期待値を C とする。
C = 下記の項の全ての和。
(1/2)×Pn×sn×2
・・・・・交換前が少額側の項
(1/2)×Pn×bn×(1/2)
・・・・・交換前が高額側の項
2×sn = bn であるので、これを書き換えると
C = 下記の項の全ての和。
(1/2)×Pn×bn
・・・・・交換前が少額側の項
(1/2)×Pn×sn
・・・・・交換前が高額側の項
こうして出来たCの計算式の中の項はEの計算式の中の項と対応が付くので、 E = C であること、すなわち交換してもしなくても同じであることがわかる。
警告! この論法をもってして二封筒問題のパラドックスが解消したと主張する人もいます。
トップページに戻る
2014/05/24 0:46:44
初版 2012/07/29
二封筒問題共通の錯覚現象とモンティ・ホール問題の錯覚との類似点
旧題:封筒を開ける前に交換型の 二封筒問題にもモンティ・ホール問題と類似の錯覚がともなっている二封筒問題の錯覚現象とモンティ・ホール問題や3囚人問題との類似点を発見したことが切っ掛けでのこのページを 2012/7/29 に書きました。
その後何度も手を加えて、2013/12/28 にようやく現在の形になりました。
封筒を開ける前に交換型の二封筒問題
ニ封筒問題は Wikipedia(英語版)の "Monty Hall problem" の記事でモンティ・ホール問題に類似したパズルとして紹介されています。
Wikipedia(英語版)の "Two envelopes problem" の記事 (17::52, 17 June 2012 の版) では、二封筒問題の問題文として、次のような問題文を採用しています。
あなたは2つの封筒を渡されたとしましょう。
どちらにもお金が入っています。
一方は他方の2倍のお金が入っています。
あなたがどちらかを選べば、それに幾ら入っていようと自分の物にすることができます。
あなたがランダムに1つを選ぶと、その封筒を開ける前に、他方に切り替える権利が与えられます。
封筒を切り替える前の金額を A として、封筒を切り替えた後の金額の期待値を計算すると A の 1.25 倍に なるので、封筒を切り替えた方が有利だということがわかります。
ところがそうすると、永久に切替え続けることが有利だという妙な結論になります。
どちらにもお金が入っています。
一方は他方の2倍のお金が入っています。
あなたがどちらかを選べば、それに幾ら入っていようと自分の物にすることができます。
あなたがランダムに1つを選ぶと、その封筒を開ける前に、他方に切り替える権利が与えられます。
封筒を切り替える前の金額を A として、封筒を切り替えた後の金額の期待値を計算すると A の 1.25 倍に なるので、封筒を切り替えた方が有利だということがわかります。
ところがそうすると、永久に切替え続けることが有利だという妙な結論になります。
このパズルは、結論が誤りであることが自明でありながら、論理のどこで勘違いしているのか簡単には分からず、ついつい、金額の確率分布から封筒を替えたときの期待値を統計数学で求めようとして、ますます混乱して来るという特徴があります。
実際は、このパズルで言うようなことは絶対にないので、統計数学を持ち出すまでもない問題ですが、そのことに自信が持てないため、「パラドックス」と呼ぶ人もいます。
結論が誤りであることが自明であるという点で自転車のパズルと似ていますが、自転車のパズルは小学生レベルの問題で、二封筒問題は大学生レベルの問題だといえそうです。 (自転車のパズルについては、モンティ・ホール問題と自転車のパズルとの共通点 でとりあげました。)
「封筒を開ける前に交換型」の二封筒問題とモンティ・ホール問題の類似点については、 封筒を開ける前に交換型の二封筒問題独自の錯覚現象 で考えました。
封筒を開けてから交換型の二封筒問題
二封筒問題には、封筒の中身を見てから交換するかしないか決める形式のものもあります。封筒を開けてから交換型のニ封筒問題は Wikipedia(英語版)の "Two envelopes problem" の記事の初版によると次のような問題です。
二人の兄弟に、計り知れないほどお金持ちのおじさんがいました。
おじさんは区別できない二つの封筒を持っています。
おじさんは、一方にある金額のお金を入れ、もう一方にその2倍の金額のお金を入れました。
それらに封をして二人の兄弟に見せました。
兄弟の一人が片方の封筒を選び、残りの兄弟がもう一方の封筒を選びました。
封筒は見分けが付かないので、彼らの選択はランダムです。
兄弟はそれぞれ自分の部屋に行き、開封しました。
兄弟の一人の封筒の金額は y でした。
彼は兄弟と封筒を交換すべきかどうかについて、次のように考えました。
交換しなければ y を得る。
自分の封筒が少額側の封筒である確率も、高額側の封筒である確率も 50% である。
したがって、封筒を交換した後の期待金額は0.5 (y/2) + 0.5 (2y) = 1.25y.
よって、封筒を交換した方が有利である。
驚いたことに彼の兄弟も同じことを考えていました。
最初の選択がランダムなのに、こんなことがどうして起きるのでしょうか?
おじさんは区別できない二つの封筒を持っています。
おじさんは、一方にある金額のお金を入れ、もう一方にその2倍の金額のお金を入れました。
それらに封をして二人の兄弟に見せました。
兄弟の一人が片方の封筒を選び、残りの兄弟がもう一方の封筒を選びました。
封筒は見分けが付かないので、彼らの選択はランダムです。
兄弟はそれぞれ自分の部屋に行き、開封しました。
兄弟の一人の封筒の金額は y でした。
彼は兄弟と封筒を交換すべきかどうかについて、次のように考えました。
交換しなければ y を得る。
自分の封筒が少額側の封筒である確率も、高額側の封筒である確率も 50% である。
したがって、封筒を交換した後の期待金額は
よって、封筒を交換した方が有利である。
驚いたことに彼の兄弟も同じことを考えていました。
最初の選択がランダムなのに、こんなことがどうして起きるのでしょうか?
注:不思議なことにWikipedia(英語版)の "Two envelopes problem" の記事の問題文が2005年ごろに封筒を開ける前に交換型の二封筒問題にすり替わっています。
Wikipedia(英語版)の "Two envelopes problem" で二封筒問題を知った私には意外でしたが、日本語でインターネット検索すると「封筒を開けてから交換型」の二封筒問題の方が多く出て来ます。
このような形式の場合、最初に選んだ封筒の金額を証拠事象とした上で、その封筒が高額側である条件付き確率や少額側である条件付き確率を考える問題になります。
そして、どちらの封筒を選んでも交換した方が有利であるような金額が封筒に入ることがあるような確率分布を考えることは簡単です。 (そのかわり、開ける前に交換するタイプとちがって、一回交換したら後もどりできません)
開けた封筒の中の金額によらず常に封筒を交換した方がよいような確率分布すらあります。 (そのような確率分布を工夫した例を、 二封筒問題のパラドキシカル分布 でとりあげました。)
「封筒を開けてから交換型」の二封筒問題とモンティ・ホール問題の類似点については、 封筒を開けてから交換型の二封筒問題はモンティ・ホール問題にもっと似ている で考えました。
「封筒を開けてから交換型」 と 「封筒を開ける前に交換型」 の錯覚現象に共通の惑わしポイント
「封筒を開けてから交換型」の二封筒問題の錯覚現象と、「封筒を開ける前に交換型」の二封筒問題の錯覚現象には、共通の惑わしポイントがあります。2013/09/13 に以下を書き加えました。
それは、封筒にだけ着目したときの大小関係と封筒の中身の金額も考慮した大小関係を同一視している点です。
そのため次のような錯覚が生じます。
あなたが選んだ封筒に A 円入っていたとすると、封筒を切り替えて手に入る金額の期待値が 1.25A円に思えてしまいます。
切り替えた後の金額の期待値 =
半分になる確率×(1/2)A +
2倍になる確率×2A=
(1/2)×(1/2)A + (1/2)×2A =
(5/4)A =1.25A
ところがこの計算式には 怪しい点があります。
封筒の中の金額 A の値に無関係に、切り替えて半分になる確率や倍になる確率がどちらも
実際に上記の数式が成立するためには次の条件が必要です。
- 封筒に入れた金額に対して、その半分の金額とのペアとその2倍の金額とのペアの両方が
同確率で発生するように制御していること
(この条件を同確率条件と呼ぶことにします)
- 金のように際限なく分割できるものを 「お金」 としていること
- 賞金の予算が無限大であること
要は、手持ちの封筒に対して、 封筒を切り替えて金額が倍になる確率と半分になる確率がどちらも
手持ちの封筒の中の金額 A に対してもそうだと勘違いしたために、 このような錯覚に陥るのです。
実際には、金額Aの入っている封筒が少額側の封筒である確率と、高額側の封筒である確率も考慮する必要があったのです。
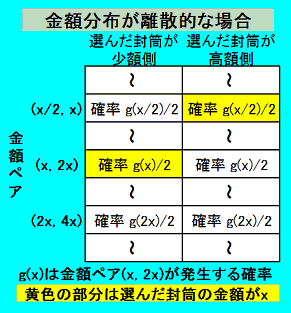
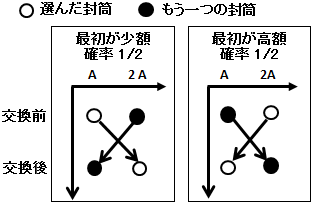
交換によって倍になる金額の確率分布と、交換によって半分になる金額の確率分布の例によって、このことを示すことができます。
| 金額分布 |
封筒を 半分や倍になる確率 |
|---|---|
|
離散的な確率分布の例 (2円,4円)のペアが確率 1/3 |
1円は倍にしかならない 2円は半分になりやすい |
|
連続な金額分布でかつ 予算に上限がある確率分布の例 |
金額の低い方では交換で倍になりやすく、 金額の高い方では半分になりやすい 注:2013/12/22 にここに書いてあったパラドキシカル分布に関する記述を下記の「補足」の項に移動しました。 |
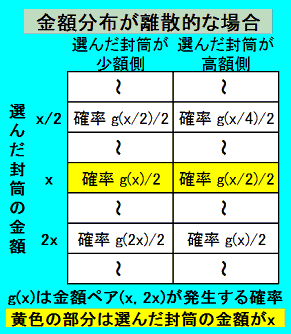
封筒に着目したときの確率が封筒の中の金額に着目したときの確率と一致するとは限らないことを、 Wagner, Carl G.(1999). を参考にしながら、数式で表現すると次のようになります。 (2014/05/12 にこの部分を書き加えました)
選んだ封筒の金額の確率変数を B 、もう一方の封筒の金額の確率変数を R とすると
P(R = B/2) = P(R = 2B) = 1/2
となるが、このことは、
P(R = (1/2) B | B = b) = P(R = 2B | B = b) = 1/2
を意味しない。
となるが、このことは、
を意味しない。
補足
純粋に数学的興味から議論するのであれば金額に上限を付けない現実離れした議論も可能です。しかし、それでもなお、同確率条件は決して成り立たないと思います。 (別ページ 二封筒問題の数学 の付録で論じています)
金額に上限を付けず、金額の平均値も無限大を許すのであれば、選んだ封筒の金額が決まった後には常に封筒を交換した方が有利な金額分布があります。そのような金額分布をパラドキシカル分布( 二封筒問題のパラドキシカル分布) と呼びますが、パラドキシカル分布でも最低金額を選んだときを除いて全域にわたって封筒を交換すると半分になりやすく、同確率条件は成立していません。
部分的同確率条件
離散的な金額分布の場合、2のべき乗を材料にして部分的に同確率条件が成立する金額分布を作ることは簡単です。連続的な金額分布の場合はどうかというと、Chalmers, D.J. (1994).に簡単な方法が示されています。
g(x) = 1/x という関数を確率密度関数の材料にして、 金額の上限下限を設定し、適当な係数を掛けて確率密度の積分が1になるようにする方法です。 (別ページ 「Chalmers の論文」 でも解説しています)
1.25 の意味
(1/2)×(1/2) + (1/2)×2 = 1.25 という計算式には 「封筒を交換したときの倍率の平均値」 という意味があります。しかし倍率は量でないので、平均値の
こういう中途半端な意味を 1.25 が持っていることが錯覚の元になっているのかも知れません。
モンティ・ホール問題との共通点 - 不適切なメンタルモデル
二封筒問題とモンティ・ホール問題の間には「不適切なメンタルモデルによる錯覚現象」という共通点あるので、これからご説明します。確率の錯覚の数学的構造はマンモグラフィの確率の錯覚の数学的構造に近いことに最近(2013年11~12月ごろ)に気づきました。 二封筒問題共通の錯覚現象とマンモグラフィの錯覚との類似点
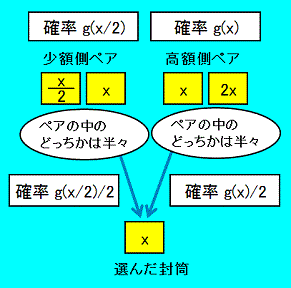
ニ封筒問題に上記のような惑わしポイントが生じるのは、問題を考えるときのメンタルモデルが不適切なためだとも考えられます。
ニ封筒問題を読んだときに思い浮かべるであろうメンタルモデルは下記の 「ニ封筒問題で錯覚を起こすメンタルモデル」 であろうと思います。
このような不適切なメンタルモデルだから、封筒を切り替えると賞金が倍になる確率と半分になる確率が 手にした封筒の金額 によらず常に
適切なメンタルモデルの方を思い浮かべれば、賞金が 2倍になる金額の分布と、半分になる金額の分布に違いがあることがすぐにわかります。
二封筒問題のメンタルモデル その1
錯覚を起こすメンタルモデル
適切なメンタルモデル
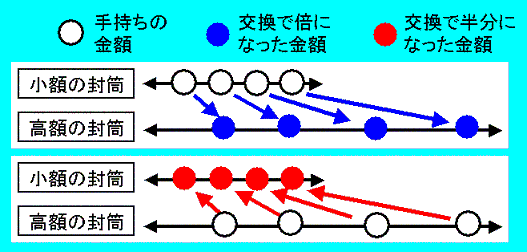
二封筒問題のメンタルモデル その2
2013/09/20 に下図を加えました。
錯覚を起こすメンタルモデル
適切なメンタルモデル (1)
金額分布が連続な場合はやや複雑なので割愛します。
適切なメンタルモデル (2)
2013/09/26 にこの図を加えました。
金額分布が連続な場合はやや複雑なので割愛します。
適切なメンタルモデル (3)
2013/12/21 にこの図を加えました。
金額分布が連続な場合はやや複雑なので割愛します。
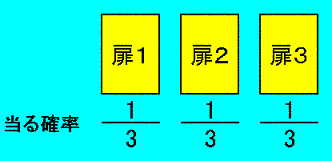
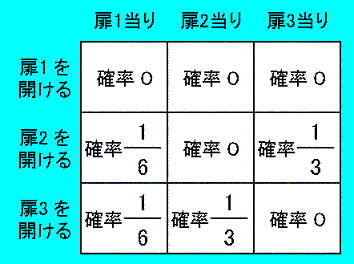
参考:モンティ・ホール問題のメンタルモデル
モンティ・ホール問題で錯覚を起こすメンタルモデル
モンティ・ホール問題で錯覚を起こさない適切なメンタルモデル
このように、「不適切なメンタルモデルによる錯覚現象」 という点で、二封筒錯覚とモンティ・ホール問題に共通するものがあります。
不適切なメンタルモデルが作られるわけ
不適切なメンタルモデルが作られるわけ その①
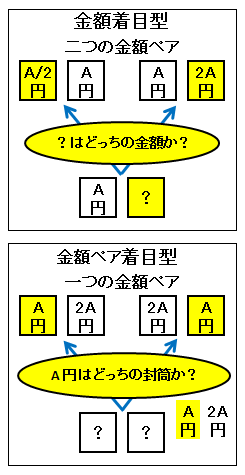
二封筒問題を解くときの考え方には次の二通りの戦略があります。この二つの戦略が頭の中で混ざり合うために、上で見たような不適切なメンタルモデルが出来上るのかも知れません。
実際、金額ペア着目型で考えるならあくまでも金額ペア着目型で貫き通し、金額着目型で考えるならあくまでも金額着目型で貫き通せば、混乱はなくなります。
「封筒を開ける前に交換型」の二封筒問題であれば金額ペア着目型で考えると、封筒を替えても替えなくても同じであることを示すことができます。
封筒を開ける前なら封筒を替えても替えなくても同じであることの金額ペア着目型説明
不適切なメンタルモデルが作られるわけ その②
心理学者による理論でも説明できそうです。- モンティ・ホール問題で、ホストが扉を開けて残った二つの扉が当たりである確率が半々であると錯覚する現象を、Fox, C.R. & Levav, J. (2004). の理論で説明できる。
- 二封筒問題で、封筒を開けた後の金額に対しても少額側か高額側かの確率が半々であると錯覚する現象を、Fox, C.R. & Levav, J. (2004). の理論の応用で説明できる。
モンティ・ホール問題にこの理論を適用すると次のようになります。
- 標本空間を { 扉1当り、扉2当り、扉3当り } の 3つに分割する。
- ホストが扉3を開けたと知らされると扉3に関する分割範囲を除外して { 扉1当り、扉2当り } という分割に修正する。
- { 扉1当り、扉2当り } のそれぞれが確率 1/2 だと錯覚する。
- 標本空間を { 選んだ封筒が高額側、選ばなかった封筒が高額側 } の 2つに分割する。
- 封筒の中の金額を変数として定めたり、封筒を開けて見て知ったりしても、その金額が高額側か少額側かまだ決まっていないため、標本空間の分割の修正ができない。
- そのため、{ 選んだ封筒が高額側、選んだ封筒が少額側 } という分割から離れられず、確率を錯覚する。
不適切なメンタルモデルが作られるわけ その③
上で見たような不適切なメンタルモデルによる錯覚現象を、「基準率錯誤」 (Base Rate Fallacy) という観点で見ることもできます。「封筒を開けてから交換型」の二封筒問題でも、「封筒を開ける前に交換型」の二封筒問題でも、選んだ封筒の金額を特定した上で、その封筒が少額側であるときにその金額である確率の計算式の中で、その封筒が 「その金額ペア」 である確率、すなわち「基準率」 が重要な位置を占めています。 (二封筒問題共通の錯覚現象とマンモグラフィの錯覚との類似点 で詳しく見ています)
このことから、二封筒問題の確率の錯覚は 「基準率錯誤」 の一種であるので、錯覚の数学的構造の面ではマンモグラフィーの錯覚の方に近いと言えます。
モンティ・ホール問題との共通点 - 証拠事象の範囲の差が問題設定の差
モンティ・ホール問題を数学の問題としてとらえる方法には最低でも下記の三つがあります。条件付確率の問題設定
不特定事象による条件付確率の問題設定
非条件付確率の問題設定
これらの問題設定の違いは条件付き確率を考えるときの証拠事象の範囲の違いです。
一方、二封筒問題の場合は、「封筒を開ける前に交換型」と「封筒を開けてから交換型」の2タイプで次のように証拠事象の範囲が違っています。
| タイプ | 証拠事象 |
|---|---|
| 封筒を開ける前に交換 | Ω(全事象) |
|
|
|
この点は、モンティ・ホール問題と二封筒問題の類似点の一つでもありますが、二封筒問題の場合、証拠事象の範囲の違いがゲームのルールの違いと対応している点が、モンティ・ホール問題の場合と大きく異なります。
モンティ・ホール問題との間に「正解を理解した後の不思議さ」という共通点はあるか?
2013/12/22 に表題と内容を書き換えました。二封筒問題とモンティ・ホール問題との間に、「確率の錯覚現象」 という共通点がありますが、数学的に理解した後の不思議さという点ではマンモグラフィーの確率の錯覚現象に近いように思います。
- モンティ・ホール問題で、ホストが扉を開けて残った二つの扉が当たる確率が半々でないことを数学的に理解すると不思議さを感じる。(私の体験から)
- マンモグラフィーで陽性反応が出た後のガンに罹っている確率が錯覚による直観より小さいことを数学的に理解しても、とりたてて不思議さの感覚がわくことはない。(私の体験から)
- 「封筒を開けてから交換型」の二封筒問題で、封筒を開けた後の金額が少額側か高額側かの確率が半々とは限らないことを数学的に理解しても、とりたてて不思議さを感じる人は少ない。(二封筒問題について述べているインターネット上のページなどを調べた結果から)
モンティ・ホール問題との共通点 - 仮説事象の現象が後に起こるという錯覚
- モンティ・ホール問題で、ホストがハズレの扉を開けた後に当たり賞品の位置が決められるかのような錯覚があります。モンティ・ホール問題を読んだ人は誰でも最初はこのような錯覚を持つものですが、中にはこの錯覚から逃れられない人も居ます。
Marilyn vos Savant の誤りを証明したつもりの人たち - 二封筒問題でも、選んだ封筒の金額が決まってから残りの封筒にお金が入れらるかのような錯覚があります。二封筒問題を読んだ人は誰でも最初はこのような錯覚を持つものです。
まとめ
二封筒問題は日常的で直観的な数学で、「つねに封筒を交換した方が良いなどということはあり得ない」 という正解を出せる問題であるにも関わらず、数学パズルとして数学好きを引き付けるのは、どういう仕掛けなのか、考えてみました。| 「期待値」などという数学好きを刺激する言葉を使うことで、 確率論の世界に人々を引きづりこむ。 |
| ↓ |
| 一つの封筒に着目した場合にその封筒が高額の封筒である確率や少額の封筒である確率を意識させる。 |
| ↓ |
| その封筒に入っている金額についても同じ確率を無意識に当てはめてしまう。 |
| ↓ |
| 計算結果が封筒を交換すべしとなって、不思議になる。 |
付録
封筒を開ける前なら封筒を替えても替えなくても同じであることの金額ペア着目型説明
金額ペア固定型の説明
例えば、金額ペア着目型で貫き通すやり方に、封筒に入っている金額の可能性を幾らだか分からないが、とにかく今現在入っているその金額に限定する金額ペア固定型の考え方があります。こういう考え方をすると金額の確率分布など関係なくなってしまい、少額の金額と高額の金額の2種類の金額に関する単純な問題になります。
二つの封筒の金額の合計を3Aとすると、
最初に選んだ封筒の金額の期待値は
(1/2) × A + (1/2) × 2A = (3/2)A
封筒を切り替えた先の金額の期待値は
(1/2) × 2A + (1/2) × A = (3/2)A
よって切り替えても切り替えなくても同じ
警告! この論法をもってして二封筒問題のパラドックスが解消したと主張する人もいます。
最初に選んだ封筒の金額の期待値は
封筒を切り替えた先の金額の期待値は
よって切り替えても切り替えなくても同じ
警告! この論法をもってして二封筒問題のパラドックスが解消したと主張する人もいます。
2013/09/26 にこの箇所を修正しました。
やや複雑ですが、金額着目型の場合も、封筒を開ける前なら封筒を替えても替えなくても同じであることを示すことができます。 (二封筒問題の数学)
金額ペア横断型説明
2013/12/22 にこの項を「封筒を開ける前なら封筒を替えても替えなくても同じであることの金額ペア着目型説明」の項の下に移動し、タイトルも変えました。金額ペア固定型の親戚の金額ペア横断型の考え方で、二つの封筒の金額の総和を固定しないで計算することもできます。
金額が離散的な場合で説明します。
金額ペアを (sn, bn) で表す。
その金額ペアの出現確率を Pn とする。
選んだ封筒に入っている金額の期待値を E とする。
E = 下記の項の全ての和。
(1/2)×Pn×sn
・・・・・少額側の項
(1/2)×Pn×bn
・・・・・高額側の項
交換した先の封筒に入っている金額の期待値を C とする。
C = 下記の項の全ての和。
(1/2)×Pn×sn×2
・・・・・交換前が少額側の項
(1/2)×Pn×bn×(1/2)
・・・・・交換前が高額側の項
2×sn = bn であるので、これを書き換えると
C = 下記の項の全ての和。
(1/2)×Pn×bn
・・・・・交換前が少額側の項
(1/2)×Pn×sn
・・・・・交換前が高額側の項
こうして出来たCの計算式の中の項はEの計算式の中の項と対応が付くので、 E = C であること、すなわち交換してもしなくても同じであることがわかる。
警告! この論法をもってして二封筒問題のパラドックスが解消したと主張する人もいます。
参考文献
-
Fox, C.R. & Levav, J. (2004).
Partition-edit-count: Naive extensional reasoning in judgment of conditional probability,
Journal of Experimental Psychology: General, 133, 626-642.
-
Chalmers, D.J. (1994).
The two-envelope paradox: A complete analysis?
-
Wagner, Carl G.(1999).
Misadventures in Conditional Expectation: The Two-Envelope Problem
Erkenntnis, Vol.51, No.2/3 (1999), pp.233–241
用語解説
-
条件付確率の問題設定
モンティ・ホール問題の問題設定の一つ。
ホストが「これこれ」のハズレ扉を開けたということを証拠事象として、
「それぞれ」の扉が当たりである条件付き確率を計算する問題設定である。
-
不特定事象による条件付確率の問題設定
モンティ・ホール問題の問題設定の一つ。
ホストが「いずれか」のハズレ扉を開けたということを証拠事象として、
「挑戦者が選んだ」扉、あるいは「残りの」扉が当たりである条件付き確率を計算する問題設定である。
-
非条件付確率の問題設定
モンティ・ホール問題の問題設定の一つ。
ホストが「いずれか」のハズレ扉を開けることは最初から分っていることとして
(相場用語なら「織り込み済み」だとして)
扉を替えないで当たりになる確率と、扉を替えて当たりになる確率を計算する問題設定である。
トップページに戻る